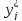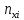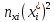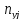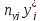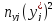Типовики по теорверу и мат статистике / Типовые расчёты
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНО УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики»
Факультет систем управления и робототехники
Типовые расчёты по теории вероятностей и математической статистике.
Выполнил студент группы № :
Проверил:
САНКТ -ПЕТЕРБУРГ 20
Типовой расчёт по теории вероятностей.
Вариант №4.
Задание №1:
Задание №2:
Задание №3:
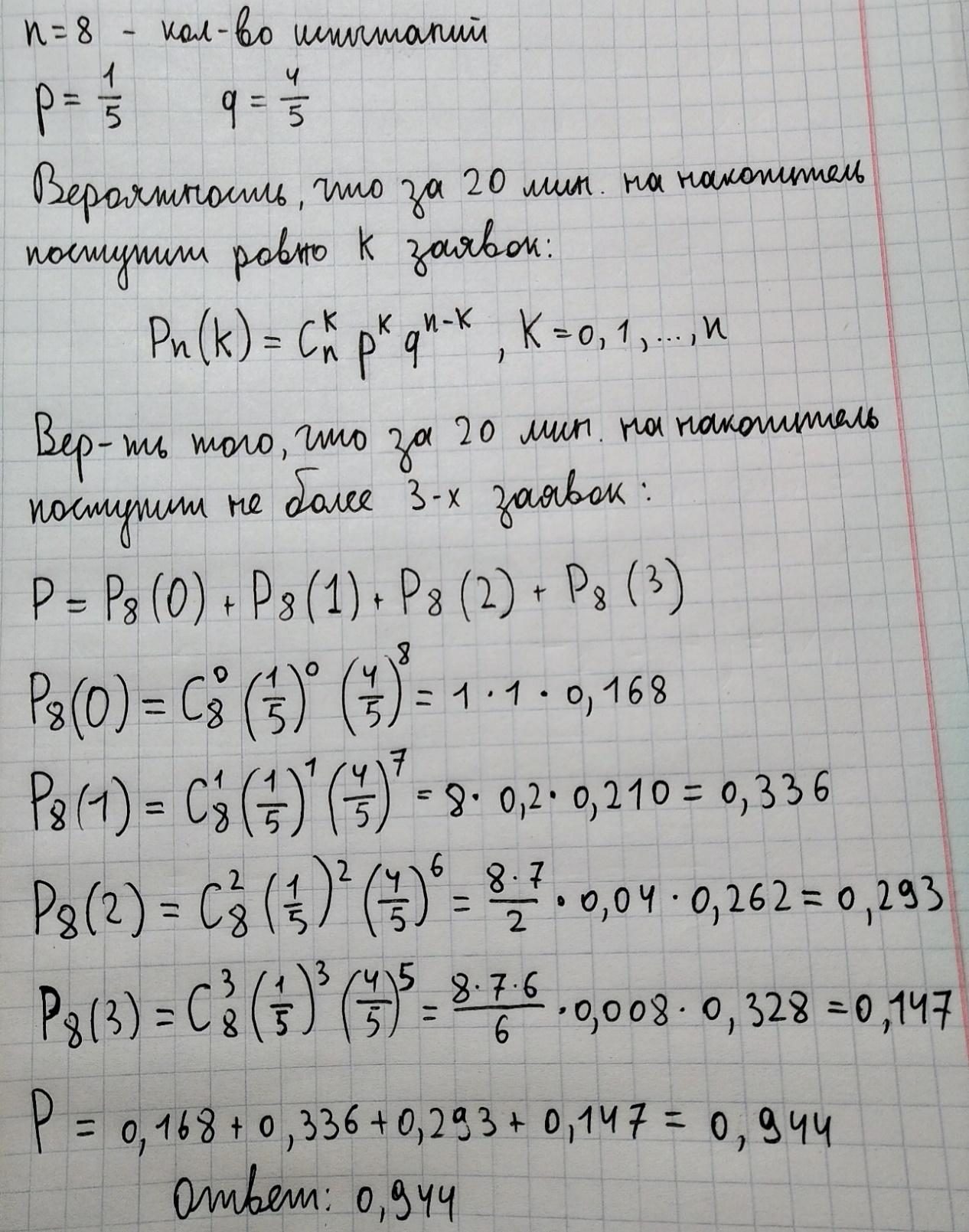
Задание №4:
Задача №5:
Типовой расчёт по математической статистике.
При выполнении этого типового расчёта я пользовался инструментами ПО «Microsoft Excel» и «Microsoft Word» для более быстрой и удобной обработки данных, построения графиков и таблиц и для написания отчёта.
Задание №1:
Из генеральной совокупности X сделана выборка объема n=200. Требуется на основании этой выборки сделать заключение о законе распределения генеральной совокупности и её основных числовых характеристиках.
Проведение группировки, построение гистограммы, ЭФР и нахождение точечных оценок математического ожидания и дисперсии.
Разобьём данные на 12 интервалов.
Наименьший
элемент:
;
Наибольший
элемент:
;
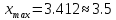Ширина
одного интервала:
.
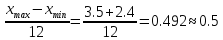Для
каждого интервала определим частоты
ni,
относительные частоты
и середины интервалов
,
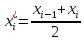i=1,2,…,12.
|
№ интер-вала |
Границы интервала |
Час-тота ni |
Относи-тельная
частота
|
|
Середина интервала
|
|
|
||||||
|
1 |
[-2,4; -1,9] |
5 |
0,025 |
0,05 |
-2,15 |
-0,0538 |
0,1260 |
||||||
|
2 |
(-1,9; -1,4] |
12 |
0,06 |
0,12 |
-1,65 |
-0,099 |
0,1827 |
||||||
|
3 |
(-1,4; -0,9] |
17 |
0,085 |
0,17 |
-1,15 |
-0,0978 |
0,1318 |
||||||
|
4 |
(-0,9; -0,4] |
31 |
0,155 |
0,31 |
-0,65 |
-0,1008 |
0,0860 |
||||||
|
5 |
(-0,4; 0,1] |
43 |
0,215 |
0,43 |
-0,15 |
-0,0323 |
0,0129 |
||||||
|
6 |
(0,1; 0,6] |
29 |
0,145 |
0,29 |
0,35 |
0,05075 |
0,0094 |
||||||
|
7 |
(0,6; 1,1] |
28 |
0,14 |
0,28 |
0,85 |
0,119 |
0,0798 |
||||||
|
8 |
(1,1; 1,6] |
19 |
0,095 |
0,19 |
1,35 |
0,12825 |
0,1496 |
||||||
|
9 |
(1,6; 2,1] |
8 |
0,04 |
0,08 |
1,85 |
0,074 |
0,1232 |
||||||
|
10 |
(2,1; 2,6] |
5 |
0,025 |
0,05 |
2,35 |
0,05875 |
0,1271 |
||||||
|
11 |
(2,6; 3,1] |
1 |
0,005 |
0,01 |
2,85 |
0,01425 |
0,0380 |
||||||
|
12 |
(3,1; 3,6] |
2 |
0,01 |
0,02 |
3,35 |
0,0335 |
0,1060 |
||||||
|
Сумма: |
200 |
1 |
|
|
0,095 |
1,1725 |
|||||||
Построим гистограмму (рис. 1).
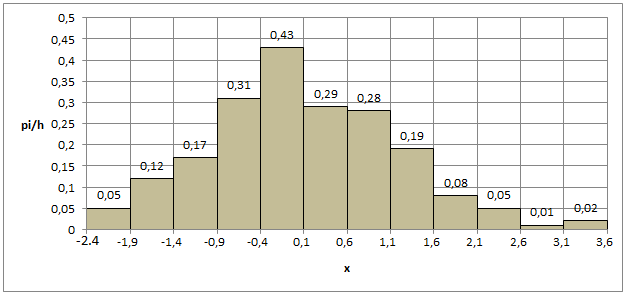
Рисунок 1 – Гистограмма распределения
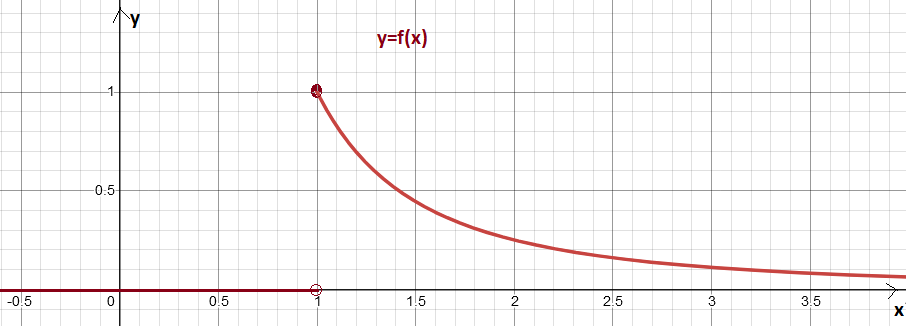
Запишем эмпирическую функцию распределения:
График эмпирической функции распределения:
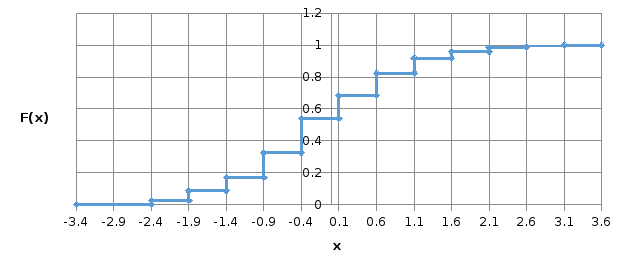
Рисунок 2 – Эмпирическая функция распределения
Найдём точечную оценку математического ожидания:
.
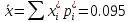Точечная оценка дисперсии:
.
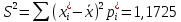Точечная оценка среднеквадратичного отклонения:
.
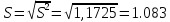Построение доверительного интервала для математического ожидания.
Доверительный интервал для математического ожидания имеет вид
.
,
,
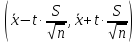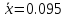при γ=0,95 Ф(t)=0.975,
откуда
t=1.95.
Получим:
.
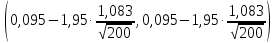(0,054, 0,244).
Таким
образом, доверительный интервал для
математического ожидания:
.
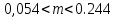Проверка статистических гипотез.
Проверим
гипотезу о том, что генеральная
совокупность, из которой произведена
выборка, имеет нормальный закон
распределения с помощью критерия
согласия χ2.
Так как математическое ожидание m
и
дисперсия σ2
генеральной совокупности нам неизвестны,
то вместо них возьмём их выборочные
характеристики: выборочное среднее
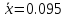и выборочную дисперсию
.
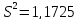Значение критерия согласия определяется по формуле
,
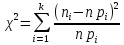где ni – число элементов выборки в каждом из k интервалов; pi – теоретическая вероятность попадания случайной величины в i-й интервал, которая определяется по формуле
Поскольку частоты последних двух интервалов малы (1 и 2), объединим 3 последние интервала в один.
|
№ интервала |
Левая граница (xi-1) |
Правая граница (xi-1) |
Частота (ni) |
|
|
|
|
|
|
|
|
1 |
- |
-1,9 |
5 |
- |
-1,842 |
0,000 |
0,033 |
0,033 |
6,5 |
0,36 |
|
2 |
-1,9 |
-1,4 |
12 |
-1,842 |
-1,381 |
0,033 |
0,084 |
0,051 |
10,2 |
0,32 |
|
3 |
-1,4 |
-0,9 |
17 |
-1,381 |
-0,919 |
0,084 |
0,179 |
0,095 |
19,1 |
0,23 |
|
4 |
-0,9 |
-0,4 |
31 |
-0,919 |
-0,457 |
0,179 |
0,324 |
0,145 |
28,9 |
0,15 |
|
5 |
-0,4 |
0,1 |
43 |
-0,457 |
0,005 |
0,324 |
0,502 |
0,178 |
35,6 |
1,53 |
|
6 |
0,1 |
0,6 |
29 |
0,005 |
0,466 |
0,502 |
0,680 |
0,178 |
35,5 |
1,20 |
|
7 |
0,6 |
1,1 |
28 |
0,466 |
0,928 |
0,680 |
0,823 |
0,144 |
28,8 |
0,02 |
|
8 |
1,1 |
1,6 |
19 |
0,928 |
1,390 |
0,823 |
0,918 |
0,094 |
18,9 |
0,00 |
|
9 |
1,6 |
2,1 |
8 |
1,390 |
1,852 |
0,918 |
0,968 |
0,050 |
10,0 |
0,42 |
|
10 |
2,1 |
+ |
8 |
1,852 |
+ |
0,968 |
1,000 |
0,032 |
6,4 |
0,40 |
|
Сумма: |
- |
- |
200 |
- |
- |
- |
- |
1 |
200 |
4,62 |
Из таблицы видим, наблюдаемое значение критерия χ2 равно 4,62.
Устанавливаем
число степеней свободы r,
которое для нормального закона вычисляем
по формуле r=k-3,
где k=10
–
количество интервалов. Значит, в нашем
случае r=7.
Назначаем уровень значимости p=0.05.
Для заданного уровня значимости p
и числа степеней свободы r
по
таблицам χ2-распределения
Пирсона находим критическое значение
критерия:
.
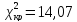Так как полученное значение χ2
=4,62
< 14.07, то
гипотеза о нормальном распределении
генеральной совокупности не отвергается.
Задание №2:
Уравнение линейной регрессии определяется по формуле
,
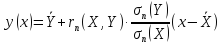где
,
,
,
.
|
|
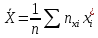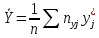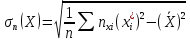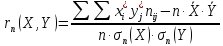21 |
31 |
36 |
41 |
|
|
|
|
16 |
0 |
0 |
30 |
80 |
110 |
1760 |
28160 |
|
26 |
0 |
55 |
20 |
0 |
75 |
1950 |
50700 |
|
36 |
15 |
0 |
0 |
0 |
15 |
540 |
19440 |
|
|
15 |
55 |
50 |
80 |
200 |
∑=4250 |
∑=98300 |
|
|
315 |
1705 |
1800 |
3280 |
∑=7100 |
|
|
|
|
6615 |
52855 |
64800 |
134480 |
∑=258750 |
|
|
\
Находим:
,
,
,
,
+
,
.
,
.
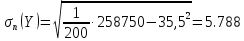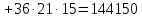
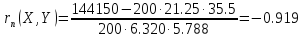
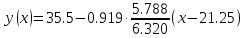
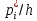
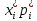
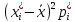
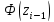
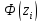
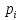
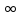
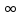
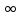
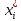