
- •Глава 3. Неопределенный интеграл
- •§ 1. Первообразная функция, неопределенный интеграл, его основные свойства
- •§ 2. Интегрирование методом замены переменной и по частям
- •§ 3. Интегрирование рациональных функций
- •§ 4. Интегрирование иррациональных функций
- •§ 5. Интегрирование тригонометрических функций
Глава 3. Неопределенный интеграл
§ 1. Первообразная функция, неопределенный интеграл, его основные свойства
В главе 2 мы решали задачи, связанные с отысканием производной данной функции. Теперь будем заниматься задачами, в которых требуется применение обратной операции, то есть по данной производной отыскивать функцию, которую дифференцировали. Операцию восстановления функции по ее производной будем называть интегрированием, а раздел математического анализа, в котором изучается эта операция и ее приложения –интегральным исчислением функции одной переменной.
Примеры практических задач, в которых применяется операция интегрирования: дана скорость движения тела, требуется найти его закон движения, то есть зависимость пройденного пути от времени; дано ускорение, требуется найти скорость движения тела; и другие.
Перейдем теперь к точным определениям.
Определение 1. Пусть на некотором
промежуткеХ задана функция![]() .
Функция
.
Функция![]() называетсяпервообразнойдля
функции
называетсяпервообразнойдля
функции![]() на этом промежутке, если для всех
на этом промежутке, если для всех![]()
![]() .
.
Заметим, что термин «первообразная» был введен французским математиком Ж.Л. Лагранжем (1736-1813).
Легко проверить, что для функций
![]() и
и![]() первообразными наR
являются функции
первообразными наR
являются функции![]() и
и![]() соответственно.
соответственно.
Теорема. Если функция![]() имеет на промежуткеХ первообразную
имеет на промежуткеХ первообразную![]() ,
то и все функции вида
,
то и все функции вида![]() будут для нее первообразными на том же
промежутке. Обратно, любая первообразная
будут для нее первообразными на том же
промежутке. Обратно, любая первообразная![]() для функции
для функции![]() ,
,![]() ,
может быть представлена в виде
,
может быть представлена в виде![]() ,
гдеС– некоторая постоянная.
,
гдеС– некоторая постоянная.
Доказательство. По определению
первообразной![]() .
Поскольку
.
Поскольку![]() ,
то
,
то![]() – первообразная для
– первообразная для![]() на промежуткеХ.
на промежуткеХ.
Пусть теперь
![]() –
любая первообразная для функции
–
любая первообразная для функции![]() наХ. Тогда
наХ. Тогда![]() наХ и согласно условию постоянства
функции на промежутке (см. главу 2)
наХ и согласно условию постоянства
функции на промежутке (см. главу 2)![]() ,
то есть
,
то есть![]() ,
где
,
где![]() .
Теорема доказана.
.
Теорема доказана.
Из доказанной теоремы следует, что
достаточно найти для данной функции
![]() только одну первообразную функцию
только одну первообразную функцию![]() ,
чтобы знать все первообразные, так как
они отличаются друг от друга постоянными
слагаемыми. Выражение
,
чтобы знать все первообразные, так как
они отличаются друг от друга постоянными
слагаемыми. Выражение![]() исчерпывает все семейство первообразных
функций для
исчерпывает все семейство первообразных
функций для![]() .
.
Определение 2. Если![]() –
первообразная для функции
–
первообразная для функции![]() ,
то выражение
,
то выражение![]() ,
гдеС – произвольная постоянная,
называетсянеопределенным интеграломот функции
,
гдеС – произвольная постоянная,
называетсянеопределенным интеграломот функции![]() и обозначается символом
и обозначается символом![]() .
.
Это обозначение ввел в 1675 году немецкий философ и математик Г.В. Лейбниц (1646-1716).
Таким образом, по определению,
![]() ,
где
,
где![]() –
первообразная для функции
–
первообразная для функции![]() ,
аС – произвольная постоянная.
,
аС – произвольная постоянная.
Функция
![]() называетсяподынтегральной функцией,
произведение
называетсяподынтегральной функцией,
произведение![]() –подынтегральным выражением,
переменнаях–переменной
интегрирования, символ
–подынтегральным выражением,
переменнаях–переменной
интегрирования, символ![]() –
знаком интеграла.
–
знаком интеграла.
Из определения неопределенного интеграла вытекают его основные свойства.
1. Производная от неопределенного
интеграла равна подынтегральной функции,
а дифференциал – подынтегральному
выражению, то есть
![]()
![]() .
.
Действительно, по определению
неопределенного интеграла имеем
![]() .
.
2. Неопределенный интеграл от производной функции равен сумме этой функции и произвольной постоянной, то есть
![]() .
(*)
.
(*)
Поскольку
![]() ,
то эту формулу можно записать в виде
,
то эту формулу можно записать в виде
![]() .
.
Формула (*) непосредственно вытекает из
определения неопределенного интеграла,
поскольку функция
![]() является первообразной для
является первообразной для![]() .
.
Таким образом, из свойств 1-2 следует,
что символы
![]() иd взаимно
уничтожаются, только во 2-ом случае к
иd взаимно
уничтожаются, только во 2-ом случае к![]() надо прибавить произвольную постояннуюС.
надо прибавить произвольную постояннуюС.
3. Постоянный множитель можно вынести
за знак неопределенного интеграла, то
есть если
![]() ,
то
,
то
![]() .
(**)
.
(**)
Действительно,
![]() ,
то есть левая и правая части равенства
(**) являются множествами всех первообразных
для одной и той же функции
,
то есть левая и правая части равенства
(**) являются множествами всех первообразных
для одной и той же функции![]() ,
значит, они равны.
,
значит, они равны.
4. Неопределенный интеграл от суммы (разности) функций равен сумме (разности) неопределенных интегралов от этих функций:
![]() .
.
Доказательство аналогично доказательству свойства 3. Это свойство справедливо и для любого конечного числа функций.
Таблица основных интегралов
1.
![]() .
8.
.
8.![]() .
.
2.
![]() .
9.
.
9.![]() .
.
3.
![]() .
10.
.
10.![]() .
.
4.
![]() .
11.
.
11.![]() .
.
5.
![]() .
12.
.
12.![]() .
.
6.
![]() .
13.
.
13.![]() .
.
7.
![]() ,
в частности,
,
в частности,![]() .
.
Заметим, что переменную х, входящую
в эти формулы, можно заменить любой
другой. Например, вместо формулы![]() можно записать
можно записать![]() и т.д.
и т.д.
Доказываются эти формулы по определению
неопределенного интеграла. Докажем,
например, формулу 4. Найдем
![]() .
Если
.
Если![]() ,
то
,
то![]() .
Если
.
Если![]() ,
то
,
то![]() .
Таким образом, формула 4 справедлива
длях, принадлежащих любому
промежутку, не содержащему нуля.
.
Таким образом, формула 4 справедлива
длях, принадлежащих любому
промежутку, не содержащему нуля.
Вычисление интегралов путем непосредственного использования таблицы простейших интегралов и их основных свойств называется непосредственным интегрированием. При этом часто приходиться производить преобразования подынтегральной функции, чтобы получить табличные интегралы.
Примеры. Вычислим интегралы: 1)![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .
.
Решение.1)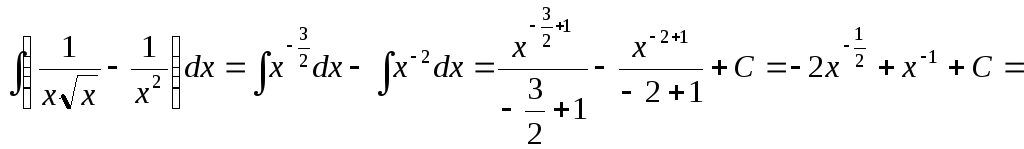
![]() .
.
2)
![]() .
.
3)
![]() .
.
Для вычисления более сложных интегралов применяются различные методы интегрирования или используются математические справочники, содержащие таблицы сложных интегралов.
