
- •§ 8. Условия постоянства, возрастания и убывания функции
- •§ 9. Экстремум функции. Наибольшее и наименьшее значения функции на отрезке
- •§ 10. Выпуклые кривые. Точки перегиба кривой
- •§ 11. Асимптоты кривой
- •§ 12. Полное исследование функций и построение их графиков
- •§ 13. Определение и свойства степени
- •§ 14. Показательная функция
- •§ 15. Логарифмическая функция
- •§16. Степенная функция
- •§ 17. Тригонометрические функции
§ 8. Условия постоянства, возрастания и убывания функции
Теорема 1 (условие постоянства
функции). Пусть функция![]() определена и непрерывна на промежуткеХ и имеет внутри него конечную
производную
определена и непрерывна на промежуткеХ и имеет внутри него конечную
производную![]() .
Для того чтобы
.
Для того чтобы![]() была постоянной наХ, необходимо
и достаточно условие
была постоянной наХ, необходимо
и достаточно условие![]() внутриХ.
внутриХ.
Доказательство.Необходимость.
Пусть
![]() на промежуткеХ. Тогда внутриХ
на промежуткеХ. Тогда внутриХ
![]() ,
то есть условие теоремы выполнено.
,
то есть условие теоремы выполнено.
Достаточность.
Зафиксируем точку
![]() и возьмем произвольную точку
и возьмем произвольную точку![]() .
К отрезку
.
К отрезку![]() применим формулу Лагранжа (6.2) (это
можно сделать, так как на этом отрезке
функция
применим формулу Лагранжа (6.2) (это
можно сделать, так как на этом отрезке
функция![]() непрерывна и внутри него имеет конечную
производную по условию теоремы), получим
непрерывна и внутри него имеет конечную
производную по условию теоремы), получим![]() ,
так как
,
так как![]() внутриХ, а
внутриХ, а![]() .
Отсюда следует, что
.
Отсюда следует, что![]() ,
т.е. постоянна наХ. Теорема доказана.
,
т.е. постоянна наХ. Теорема доказана.
Теорема 2 (условие монотонности
функции). Пусть функция![]() определена и непрерывна на промежуткеХ и имеет внутри него конечную
производную
определена и непрерывна на промежуткеХ и имеет внутри него конечную
производную![]() .
Для того чтобы
.
Для того чтобы![]() была наХнеубывающей (невозрастающей),
необходимо и достаточно условие
была наХнеубывающей (невозрастающей),
необходимо и достаточно условие![]() внутриХ.
внутриХ.
Доказательство. Рассмотрим случай неубывающей функции.
Необходимость. Пусть функция![]() не убывает наХ. Возьмем внутри
промежуткаХ произвольную точкухи
не убывает наХ. Возьмем внутри
промежуткаХ произвольную точкухи![]() .
Тогда
.
Тогда![]() и, переходя в последнем неравенстве к
пределу при
и, переходя в последнем неравенстве к
пределу при![]() ,
получим
,
получим![]() .
.
Достаточность. Пусть![]() внутриХ. Возьмем произвольные
точки
внутриХ. Возьмем произвольные
точки![]() ,
,![]() и применим формулу Лагранжа (6.2) на
отрезке
и применим формулу Лагранжа (6.2) на
отрезке![]() :
:![]()
![]() ,
так как
,
так как![]() .
Поэтому
.
Поэтому![]() ,
то есть функция
,
то есть функция![]() является неубывающей.
является неубывающей.
Аналогично рассматривается случай невозрастающей функции. Теорема доказана.
Теорема 3 (достаточное условие
строгой монотонности функции). Если
функция![]() определена и непрерывна на промежуткеХ, внутри него имеет конечную
производную
определена и непрерывна на промежуткеХ, внутри него имеет конечную
производную![]() и всюду внутриХ
и всюду внутриХ ![]() ,
то
,
то![]() строго возрастает (убывает) наХ.
строго возрастает (убывает) наХ.
Доказательство. Возьмем произвольные
точки![]() ,
,![]() и применим к
и применим к![]() на отрезке
на отрезке![]() формулу Лагранжа (6.2):
формулу Лагранжа (6.2):![]()
![]() ,
где
,
где![]() .
Поскольку
.
Поскольку![]() ,
из условия
,
из условия![]() следует, что
следует, что![]() ,
то есть
,
то есть![]() строго возрастает, а из условия
строго возрастает, а из условия![]() следует, что
следует, что![]() ,
то есть
,
то есть![]() строго убывает. Теорема доказана.
строго убывает. Теорема доказана.
Замечание. Условие![]() не является необходимым для строгого
возрастания (убывания) функции
не является необходимым для строгого
возрастания (убывания) функции![]() .
Например, для функции
.
Например, для функции![]() в точке
в точке![]() ,
в то же время эта функция строго возрастает
на всей числовой прямой. Вообще, если
,
в то же время эта функция строго возрастает
на всей числовой прямой. Вообще, если![]() обращается в нуль в конечном числе
точек, а в остальных точках сохраняет
знак, то
обращается в нуль в конечном числе
точек, а в остальных точках сохраняет
знак, то![]() –
строго монотонная функция. Для
доказательства этого достаточно
применить формулу Лагранжа к промежуткам
между соседними нулями производной.
–
строго монотонная функция. Для
доказательства этого достаточно
применить формулу Лагранжа к промежуткам
между соседними нулями производной.
Определение 1. Функция![]() называетсявозрастающей (убывающей)в точке
называетсявозрастающей (убывающей)в точке
![]() ,
если существует окрестность
,
если существует окрестность![]() точки
точки
![]() такая, что функция определена в этой
окрестности и знак приращения функции
такая, что функция определена в этой
окрестности и знак приращения функции![]() в этой окрестности совпадает со знаком
(противоположен знаку) приращения
аргумента.
в этой окрестности совпадает со знаком
(противоположен знаку) приращения
аргумента.
у
![]()
Если
для
для
поэтому функция
в точке
![]() ,
то
,
то![]() ,
,![]() ,
,![]() возрастает
возрастает![]() .
.


О
◦ ◦![]() х
х

Теорема 4 (достаточное условие
монотонности функции в точке). Если
функция![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки![]() и имеет в этой точке положительную
производную
и имеет в этой точке положительную
производную![]() ,
то функция
,
то функция![]() возрастает в точке
возрастает в точке![]() .
Если же
.
Если же![]() ,
то
,
то![]() убывает в точке
убывает в точке![]() .
.
Доказательство. В силу теоремы 1 § 2
![]() ,
где
,
где![]() при
при![]() .
Поскольку
.
Поскольку![]() при
при![]() ,
а
,
а![]() ,
существует
,
существует![]() такое, что
такое, что![]() при
при![]() или
или![]() .
Если
.
Если![]() ,
то в окрестности
,
то в окрестности![]()
![]() ,
откуда
,
откуда![]() и знак
и знак![]() совпадает со знаком
совпадает со знаком![]() ,
т.е. функция
,
т.е. функция![]() возрастает в точке
возрастает в точке![]() .
Если
.
Если![]() ,
то
,
то![]() ,
откуда
,
откуда![]() и знак
и знак![]() противоположен знаку
противоположен знаку![]() ,
т.е. функция
,
т.е. функция![]() убывает в точке
убывает в точке![]() .
Теорема доказана.
.
Теорема доказана.
Пример. Найдем интервалы монотонности
функции![]() .
.
Решение. Найдем область определения
функции: функция существует, когда![]() и
и![]() ,
то есть
,
то есть![]() .
Далее,
.
Далее,![]() =
=![]() ,
в области определения
,
в области определения![]() существует. Отметим на числовой прямой
область определения функции и точку
существует. Отметим на числовой прямой
область определения функции и точку![]() ,
в которой производная равна нулю. После
этого определим в каждом из полученных
промежутков знак производной с помощью
пробных точек:
,
в которой производная равна нулю. После
этого определим в каждом из полученных
промежутков знак производной с помощью
пробных точек:![]() ,
,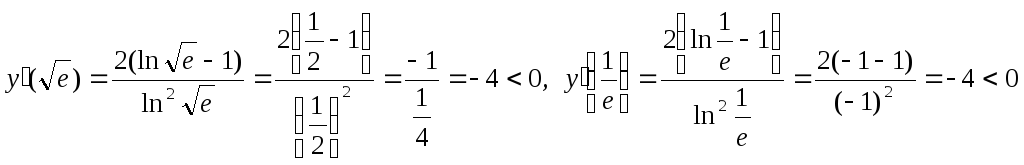 .
.
– – +
![]()

![]()
0 1 е
Видим, что функция убывает на интервалах
(0; 1) и (1; е), возрастает на интервале![]() .
.
