Глава 2. Дифференциальное исчисление функций одной и нескольких переменных

§ 1. Определение производной. Ее механический и геометрический смысл. Уравнения касательной и нормали к кривой

Рассмотрим сначала две задачи, приводящие к понятию производной.

1. Задача о вычислении скорости движущейся точки.

Пусть по прямой движется точка, уравнение движения которой выражает зависимость величины пути, пройденной точкой, от времени. Требуется определить скорость движения точки в момент времени.

расстояние, пройденное точкой за время ,ОМ– расстояние, пройденное за времяt,– расстояние, пройденное за время, то есть за промежуток времени. Ясно, что. Средняя скорость точки на участке путиравна. Ясно, что при уменьшениисредняя скорость будет приближаться к скорости точки в момент, поэтому скоростью точки в момент времениназывается предел отношенияпри:

.

Таким образом,

. (1.1)

2. Задача о проведении касательной к кривой.

Пусть дана некоторая кривая L. Дадим сначала определение касательной к кривойLв точкеМ. Для этого возьмем на кривой точкуN и проведем секущуюMN. Затем,

у оставляя точкуМ неподвижной, будем двигать

N точкуN по кривой к точкеМ. СекущаяMN при

этом будет поворачиваться вокруг точки М. Если

Lона пристремится к некоторому

предельному положениюМР, то это предельное

Рположение секущей и называется касательной к

кривой в точке М.

М Определение 1. ПрямаяМРназываетсякасательнойк кривойLв точкеМ, если угол

Ох между нею и секущей стремится к нулю при

неограниченном приближении по кривой точки Nк точкеМ.

Найдем уравнение касательной к кривой в точке. Ясно, что для

этого достаточно найти ее угловой коэффициент , поскольку точкаМ, через которую проходит касательная, дана. Уравнение, как известно из аналитической геометрии, имеет вид

. (1.2)

к нулю. Таким образом,

. (1.3)

Сравним формулы (1.1) и (1.3). Видим, что в этих формулах мы делаем одно и то же: вычисляем приращение функции, соответствующее приращению аргумента или, составляем их отношение и переходим к пределу приили, только функции в этих формулах имеют разный смысл – величина пути и ордината точки. Выделяя общее в рассмотренных задачах, абстрагируясь от их конкретного содержания, приходим к понятию производной.

Определение 2.Производнойфункциив точкеназывается предел отношения приращения функции в этой точке к вызвавшему его приращению аргумента при условии, что приращение аргумента стремится к нулю. Обозначается производнаяи т.д.

Таким образом,

.

Возвращаясь к задачам, видим, что , то есть скоростьVесть производная от пройденного путиS по времениt;, то есть угловой коэффициент касательной к кривойесть производная от ординатыпо абсциссех. Из этих фактов вытекает механический и геометрический смысл производной.

Механический смысл производной: производная – это скорость изменения переменнойотносительно переменнойх.

Геометрический смысл производной: производная есть угловой коэффициент касательной к кривойв точке, то есть тангенс угла между

касательной и положительным направлением оси Ох.

Пример 1. Найдем производные функций,,.

Решение. Воспользуемся определение производной. Получим

, так как~ ~при. В частности,;

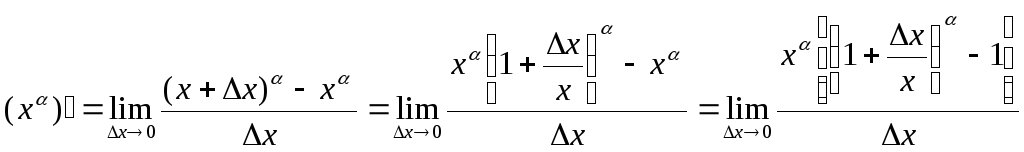=, так как~при;

, так как~при;

, так как~при;

;

.

Из формулы (1.2) получаем уравнение касательной к кривой в точке:

или. (1.4)

Определение 3. Прямая, проходящая через точку касанияперпендикулярно к касательной, называетсянормалью к кривой в этой точке.

Из аналитической геометрии известно, что ее угловой коэффициент , поэтому уравнение нормали имеет вид

. (1.5)

Пример 2. Напишем уравнения касательной и нормали к кривойв точке (1;е).

Решение. Поскольку, по формулам (1.4) и (1.5) находим

– уравнение касательной к данной кривой в данной точке,– уравнение нормали к данной кривой в данной точке.

Может оказаться так, что предел в определении производной не существует. В этом случае говорят, что функция производной в точкене имеет. Однако может оказаться так, что односторонние пределы существуют, но не равны. В этом случае говорят об односторонней производной функции в точкесправа или слева. К односторонней производной мы приходим и тогда, когда точкаявляется концом промежутка. Обозначают односторонние производныеи.

В случае, когда производная функции не существует, но существуют односторонние производные, говорят также об односторонних касательных к кривой в соответствующей точке кривой. Если же производная бесконечна, то касательная к кривой в соответствующей точке параллельна оси Оу.

Определение 4. Операция отыскания производной называетсядифференцированием. Раздел математического анализа, главным предметом которого является вычисление производных, изучение и использование их свойств, называетсядифференциальным исчислением.