Лекция №3

2. АРИФМЕТИЧЕСКИЕ ОСНОВЫ ЭВМ

2.1. Представление числовой информации. Системы счисления.

Все современные ЭВМ имеют развитую систему арифметических команд, включающую десятки и сотни машинных операций. Однако выполнение любой такой операции основано на использовании простейших микроопераций типа

сложения и сдвига чисел.

При обработке информации (в том числе и чисел) в ВМ используются специальные коды для ее представления. Для кодирования символов используется определенное количество двоичных разрядов. Набор из n двоичных разрядов позволяет представить алфавит из 2n символов. Так например, с помощью одного байта можно кодировать символы алфавита, состоящего из 28 = 256 различных символов. При этом возможны и практически применяются различные кодировки или кодовые таблицы соответствия двоичных кодов конкретным символам: ASCII, КОИ-8, Windows-1251 и другие. В настоящее время широко используется двухбайтовая кодировка Unicode.

Числовая иформация в ЭВМ всегда представляется в той или иной системе счисления. Под системой счисления понимается совокупность символов и правил их записи, применяемых для однозначной записи чисел.

Выбор системы счисления – один из важнейших вопросов. От правильности его решения зависят такие характеристики ВМ как простота технической реализации, помехоустойчивость кодирования цифр, скорость вычислений, сложность алгоритмов реализации арифметических операций, удобство работы и другие. По совокупности такого рода показателей, в современных ВМ, используется так называемая двоичная система счисления.

Все системы счисления подразделяются на позиционные и непозиционные. Непозиционной называется такая система счисления, в которой значение цифры не зависит от ее положения в ряду цифр, изображающих число. Примером является римская система счисления, в которой для обозначения отдельных чисел используются буквы римского алфавита. Цифры в римской системе обозначаются различными знаками: 1 – I, 3 – III, 5 – V, 10

– X, 50 – L, 100 – С, 500 – D, 1000 – М. Запись числа осуществляется по правилу: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а слева – вычитается из него: так, ХС – 90, СХ – ПО, MCMLXXXVIII – 1988. Выполнять арифметические действия в непозиционных системах неудобно. Поэтому в настоящее время эти системы не используются для расчетов.

Позиционной системой счисления (ПСС) называется такая система счисления, в которой значение цифры зависит от ее положения в ряду цифр, изображающих число. В этой системе число представляется в виде полинома n-ой степени, а изображается совокупностью некоторых символов, каждый из которых имеет различный вес в зависимости от позиции, которую он занимает. Вес символа определяется как целая степень некоторого числа – основания системы. Позиция символа называется разрядом.

Основание системы счисления – мощность множества различных символов, допустимых в каждой позиции числа. Так для десятичной системы допускаемыми являются символы: 0, 1, 2, 3, ..., 9.

Обозначим через p основание системы счисления. Числа в позиционных системах счисления представляются последовательностью цифр (разрядов), разделенных запятой на две группы: группу разрядов, изображающую целую часть числа, и группу разрядов, изображающую дробную часть числа: X а n а n 1 а 2 а1 а 0 , а 1 а 2 а m .

Здесь а n , а n 1 , , а 0 , а1 обозначают цифры n-го, n-1 и т.д. разрядов целой части числа, а1 , а 2 , , а m 1 , а m – цифры первого, второго и т.д. разрядов дробной части числа.

Единице каждого разряда приписан определенный вес pk, где k – номер разряда, равный индексу при буквах, изображающих цифры разрядов. Основание системы счисления показывает, во сколько раз вес i-го разряда больше i-1 разряда. Так, представленная запись означает следующее:

X a

n

p n a

n 1

p n 1 ... a

0

p 0

a

1

p 1 ... a

m

p m

(0.0.1)

Например: 1 2 3 5 , 8 7

1 0

1 1 0 3

2 1 0 2 5 1 0 0

8 1 0 1 7 1 0 2 . Максимальное число кото-

рое может быть представлено в m разрядах

N

m a x

p m 1, минимальное число не равное

нулю, которое может быть записано в s разрядах дробной части N

m in

p s . При работе с

ЭВМ широко применяют ПСС с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную. В обычной практике повсеместно используется десятичная система счисления.

Десятичная система счисления.

В десятичной системе счисления основанием системы является число 10. Для записи любого числа в этой системе используются цифры от 0 до 9. При указании десятичной системы счисления используют символ d: 67d.

Двоичная система счисления.

Для записи цифр разрядов двоичного числа требуется набор всего лишь из двух символов, в качестве которых используются 0 и 1. Следовательно, в двоичной системе счисления число представляется последовательностью символов 0 и 1. Будем использовать запись 11011,1012 или 11011,101b при записи двоичных чисел.

Восьмеричная и шестнадцатеричная системы счисления.

Восьмеричная и шестнадцатеричная системы используются для компактного, и значит более удобного человеку, отображения двоичных чисел. Основанием системы счисления является 8(16) и для записи цифр разрядов должен использоваться набор из восьми (шестнадцати) символов: 0, 1, 2,..., 7 (0, 1, 2,..., 9, А, В, С, D, Е, F).

В шестнадцатеричной системе символ А соответствует количеству, в десятичной системе счисления равному 10, В – 11, С – 12, D – 13, Е – 14 и F – 15. При указании, восьмеричной (шестнадцатеричной) системы счисления будем использовать символы o(h)

или нижний индекс 8(16): 7 3 5 ,4 8 7 3 5 ,4 d , A B 9, C 2 F1 6 A B 9, C 2 F h .

В табл. 3.1 показано соответствие записи чисел в десятичной, восьмеричной и шестнадцатеричной системах счисления.

X10	X2	X8	X16
0	0000	0	00
1	0001	1	01
2	0010	2	02
3	0011	3	03
4	0100	4	04
5	0101	5	05
6	0110	6	06
7	0111	7	07
8	1000	10	08
9	1001	11	09
10	1010	12	0A
11	1011	13	0B
12	1100	14	0C
13	1101	15	0D
14	1110	16	0E
15	1111	17	0F
16	1000	20	10

Таблица 3.1. Запись чисел в разных системах счисления

Еще раз отметим, что шестнадцатеричные и восьмеричные числа – это только способ представления больших двоичных чисел, которыми фактически оперирует процессор. При этом шестнадцатеричная система оказывается предпочтительнее, поскольку в современных ЭВМ процессоры манипулируют словами длиной 4, 8, 16, 32 или 64 бита, т.е. длиной слов, кратной 4. В восьмеричной же системе счисления предпочтительны слова, кратные 3 битам, например, слова длиной 12 бит (как в PDP-8 фирмы DEC).

2.2.Двоичная система счисления. Перевод чисел из одной системы счисления в другую.

Двоичная ПСС получила самое широкое применение в ЭВМ из-за того, что в ЭВМ числовая информация отождествляется с состоянием используемых двоичных физических элементов. В двоичной ПСС a i 0 ,1 поэтому для физического представления числа а,

достаточно использования элементов с двумя устойчивыми состояниями, кодируемыми 1 и 0. Очевидно, что реализация элементов, которые должны различать одно из двух состояний, оказывается проще, надежнее и дешевле, чем реализация элементов, которые должны различать одно из 10 состояний.

Арифметические операции в двоичной системе счисления выполняются по тем же правилам, что и в десятичной системе счисления.

Сложение	Вычитание		Умножение
0+0=0	0	0=0	0·0=0
0+1=1	1	0=1	0·1=0
1+0=1	1	1=0	1·0=0
1+1=10	10	1=1	1·1=1

С другой стороны громоздкость записи чисел в двоичной ПСС и трудность их восприятия человеком приводит к необходимости перевода исходных данных (чисел) из десятичной системы счисления в двоичную, а результатов – из двоичной в десятичную. Эти переводы осуществляются в ЭВМ автоматически по определенным алгоритмам.

2.2.1. Перевод числа из десятичной системы счисления

		Пусть N – целое десятичное число. Запишем его в виде (0.0.1). На первом шаге разде-
лим число					N на		основание системы p. Частное от деления будет равно:
a	n	p n a	n 1	p n 1	... a	,	а остаток равен a0. На втором шаге целое частное опять разделим на
					1

p, остаток от деления будет теперь равен a1. Если продолжать этот процесс деления, то после n-го шага получим последовательность остатков: a0, a1,…, an.

Эта последовательность совпадает с обратной последовательностью цифр целого двоичного числа. Таким образом, достаточно записать остатки в обратной последовательности, чтобы получить искомое двоичное число. Тогда сам алгоритм будет следующим:

Метод деления. Для перевода целого числа из десятичной системы счисления в любую другую ПСС необходимо разделить десятичное число на основание новой системы счисления, затем полученное частное снова разделить на основание новой системы счисления и так до тех пор, пока в частном не останется число меньше основания новой системы счисления. Число в новой системе счисления запишется в виде остатков от деления, начиная с последнего частного, представляющего собой старшую цифру числа. Поясним это на примере.

Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

		Таким образом, 7510 =10010112 =1138 = 4B16.
		Пусть X – правильная десятичная дробь. Запишем ее в виде (0.0.1). На первом шаге
умножим					число		X	на основание системы p. Произведение будет равно:
a	1	a	2	p 1	... a	s	p s 1 ,	и целая часть будет равна a-1. На втором шаге оставшуюся дроб-

ную часть опять умножим на p, получим целую часть, равную a-1. Описанный процесс необходимо продолжать до тех пор, пока в результате умножения мы не получим нулевую дробную часть или не будет достигнута требуемая точность вычислений.

Эта последовательность совпадает с обратной последовательностью цифр целого двоичного числа. Таким образом, достаточно записать остатки в обратной последовательности, чтобы получить искомое двоичное число. Тогда сам алгоритм будет следующим:

Метод умножения. Для перевода правильной десятичной дроби в другую систему счисления необходимо дробную часть десятичного числа последовательно умножать на основание новой системы счисления, представленное в исходной ПСС. В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления до тех пор, пока в дробной части не останутся нули или не будет достигнута заданная точность перевода.

Правильная десятичная дробь точно представима конечной p-ичной дробью, если существует натуральное число, при умножении на которое знаменателя дроби можно получить некоторую натуральную степень числа p. Если же такого числа не сущесвует, то в p- ичной системе дробь окажется бесконечной. Это правило следует из формулы (0.0.1).

Если требуемая точность перевода числа составляет k знаков после запятой, то предельная абсолютная погрешность (напомним, что это число не меньшее чем абсоютная

погрешность) при этом равняется p k 1 / 2 .

Пример: Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Получаем, что 0,3610≈0,010112≈0,2708≈0,5С16.

Неправильные дроби десятичной системы счисления в любую другую переводятся в два приема: целая часть переводится по первому правилу, дробная по второму. Затем целую и дробную части числа записывают вместе, отделяя запятой.

2.2.2. Перевод числа в десятичную систему.

Перевод чисел в десятичную ПСС из любой другой ПСС удобнее всего производить, представляя эти числа в развернутой форме (0.0.1):

1 1 0 1 0 0 12 1 2 6 1 2 5 0 2 4 1 2 3 0 2 2 0 2 1 1 2 0 1 0 5 1 0.

При вычислении десятичного значения p-ичного числа удобно использовать так называемую «схему Горнера», которая позволяет получить результат с использованием минимального числа арифметических операций сложения и умножения. Схема Горнера основана на следующих тождественных преобразованиях исходного многочлена (0.0.1):

a

n

p n a

n 1

p n 1

... a

1

p a

0

( a

n

p a

n 1

) p n 1 a

n 2

p n 2

... a

1

p a

0

( ( a

n

p a

n

1

) p a

n

2

) p n 2

a

n 3

p n 3 .... a

1

p a

0

...

( ...( a n p a n 1 )

p a n 2

) p a n 3 ) p

.... a1 ) p

a 0 .

Соответственно дробная часть числа переводится в десятичное число по схеме Горнера следующим образом:

a

1

p 1

a

2

p 2

... a

m

p

m

( a

m

p 1

a

m 1

) p m 1 a

m 2

p m 2

... a

1

p 1

( ( a

m

p

1

a

m 1

) p 1 a

m 2

) p m 2

a

m 3

p m 3 .... a

1

p 1

...

( ...( a

m

p

1

a

m 1

) p 1

a

m 2

) p 1

a

m 3

) p 1

.... a

1

) p 1 .

2.2.3. Перевод в двоичную систему счисления восьмеричных и шестнадцатеричных чисел и наоборот.

Правила перевода восьмеричных и шестнадцатеричных чисел в двоичные и наоборот исключительно просты, поскольку основания восьмеричной и шестнадцатеричной систем счисления есть целые степени числа (8 = 23,16 = 24).

Для перевода восьмеричного (шестнадцатеричного) числа в двоичную форму доста-

точно заменить каждую цифру этого числа трехразрядным (четырехразрядным) двоичным числом:

2 5 1 6 ,18 0 1 0 1 0 1 0 0 1 1 1 0 , 0 0 12 7 B 3, E1 6 0 1 1 1 1 1 0 0 0 0 1 1,1 1 1 0 2

При переводе из двоичной в восьмеричную (шестнадцатеричную) систему поступа-

ют следующим образом: двигаясь от запятой влево и вправо, разбивают двоичное число на группы по три (триада) или четыре (тетрада) разряда, дополняя при необходимости, нулями крайние левую и правую группы. Затем каждую группу из трех (четырех) разрядов заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой:

0 1 1 0 0 1 1 1 1,1 1 0 1 0 0 2 3 1 7 , 6 4 8 , 0 0 1 1 0 0 0 1,1 0 1 1 1 0 0 0 2 3 1, B 8 1 6.

2.3.Машинное представление чисел. Числа с фиксированной и плавающей запятой. Стандарт IEEE 754.

Все числа в ЭВМ хранятся и обрабатываются в соответствии с рядом правил. Во-пер- вых, в ЭВМ фиксируется количество двоичных разрядов, предназначенных для хранения и обработки чисел. Это количество байтов называется разрядной сеткой машины. Начиная с вычислительных машин 2-го поколения, разрядная сетка ЭВМ кратна байту.

В ЭВМ не может быть представлено число, содержащее большее количество двоичных разрядов, чем их имеется в разрядной сетке машины. Это накладывает ограничение на возможную точность расчетов: чем больше разрядная сетка, тем более высокая точность вычисления может быть обеспечена.

Во-вторых, все числа в ЭВМ представлены в некоторой форме. Используется две формы представления чисел: естественная (форма с фиксированной запятой) и нормальная (форма с плавающей запятой).

В-третьих, все числа перед размещением в памяти ЭВМ масштабируются. Если обозначить через [X] машинное представление числа X, то масштабирование означает умножение на некоторый коэффициент [X]kX, величина которого зависит, в том числе и от формы представления числа в ЭВМ.

По очевидным причинам, множество машинных чисел в какой-либо разрядной сетке принадлежит интервалу: X m in [ X ] X m a x . Числа, выходящие за границы этого интервала,

не могут быть представлены в ЭВМ. При попытке записи таких чисел говорят о перепол-

нении разрядной сетки.

И последнее – число может быть закодировано, т.е. преобразовано в специальный двоичный вид, с тем, чтобы получить определенные выгоды при его обработке и хранении. В ЭВМ с помощью применения специальных машинных кодов чисел все арифметические операции над числами сводятся к операциям арифметического сложения и сдвига кодов.

При естественной форме число записывается в естественном натуральном виде с выделением в общем случае следующих компонент числа: знака, запятой и цифр числа. В форме с фиксированной запятой в разрядной сетке выделяется строго определенное число разрядов для целой и для дробной частей числа. Левый (старший) разряд хранит признак знака (0 – «+», 1 – «-» ) и для записи числа не используется.

В большинстве ЭВМ числа с фиксированной запятой, с которыми оперирует машина, представлены в виде правильных дробей, т.е. запятую фиксируют перед старшим разрядом числа, причем числа, больше единицы, приводятся к такому виду при помощи масштабного коэффициента. Представление чисел в виде правильных дробей обусловлено необходимостью уменьшить возможность переполнения разрядной сетки машины, т.е. уменьшить опасность потери значащих цифр старших разрядов при выполнении арифметических операций. В этом случае результат умножения никогда не выходит за пределы разрядной сетки, а вероятность переполнения при их сложении мала. Однако это приводит к снижению точности представления чисел и точности вычислений.

Нередко запятую фиксируют после младшего разряда числа. Тогда все данные представляются в виде целых чисел. В этом случае также необходимо масштабирование исходных данных. Если точка фиксируется перед первой значащей цифрой, то диапазон из-

менения положительных значений определяется неравенством 2 n X 1 2 n . Диапазон изменения положительных чисел, где точка фиксируется после последней значащей цифры, составляет: 0 X 2 n 1 .

Форма представления чисел с фиксированной запятой упрощает аппаратную реализацию ЭВМ, уменьшает время выполнения машинных операций, однако при решении задач на машине необходимо постоянно следить за тем, чтобы все исходные данные, промежуточные и окончательные результаты находились в допустимом диапазоне представления. Если этого не соблюдать, то возможно переполнение разрядной сетки, и результат вычислений будет неверным. В современных компьютерах форма представления чисел с фиксированной запятой используется только для целых чисел.

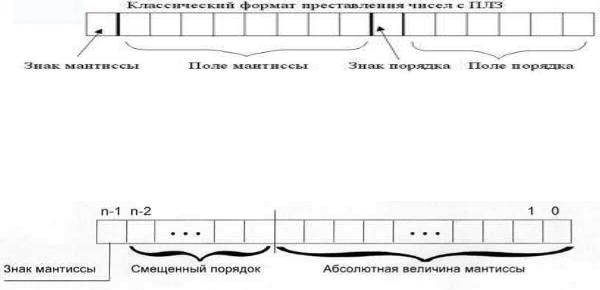
От этих недостатков в значительной степени свободны ЭВМ, использующие форму представления чисел с плавающей запятой, или нормальную форму. Нормальная форма записи числа может быть представлена в виде ±mp±q, где m – называется мантиссой числа, q – порядком числа, а p есть основание ПСС.

Порядок (с учетом знака) показывает, на сколько разрядов и в какую сторону сдвинута запятая при замене формы записи числа с естественной на нормальную. Поэтому такую форму записи называют представлением чисел с плавающей запятой. Такая форма за-

писи имеет недостаток: некоторые числа записываются неоднозначно (например, 0,0001 можно записать – 0,0001·102, 0,001·10−1, 0,01·10−2, 0,1·10−3 и т.д.). Поэтому распространены также другие формы записи – нормализованная, в которой мантисса числа 1≤m<p и денормализованная, в которой мантисса числа 1/p≤m<1.

Для представления числа в нормальной форме в слове данных выделяют четыре структурных компонента: два поля знаков (мантиссы и порядка) и два поля цифр.

Для того, чтобы не хранить знак порядка, используется так называемый смещенный порядок, который рассчитывается по формуле 2k-1-1+ИП, где k – количество разрядов, отводимых под порядок, ИП – истинный порядок.

Все компьютеры поддерживают несколько международных стандартных форматов, различающихся по точности, но имеющих одинаковую структуру следующего вида:

Для 32-х разрядной сетки, в соответствии с международным стандартом IEEE 754 формат числа с плавающей запятой состоит из трех полей. Первое поле (31-й бит) хранит знак числа (s), второе поле, размещенное в битах с номерами 30, ..., 23, смещенный порядок. Третье поле из оставшихся 23 битов с номерами 22, ..., 0 отводится под мантиссу.

s		смещенный по-																мантисса
				рядок
31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14	13	12	11	10	09	08	07	06	05	04	03	02	01	00
					Таблица 3.3.1. Разрядная сетка для представления числа с плавающей точкой

Теперь опишем алгоритм перевода числа с плавающей точкой во внутреннее представление по стандарту IEEE 754 для 32-х разрядной сетки.

1.Переводимое число положительно? Да – переход на шаг 2. Иначе – переход на шаг 3.

2.Выставить в 31-й разряд 0. Переход на шаг 4.

3.Выставить в 31-й разряд 1.

4.Перевести число в двоичную ПСС.

5.Привести число к нормализованному виду (т.е. 1, a1 a 2 ...a n ...(1 0 2 ) q ) и определить из него двоичный порядок q.

6.Вычислить смещенный двоичный порядок q' = 11111112+q. Записать его в разряды с 30 по 23.

Пример. Получить машинное представление в 32-х разрядной сетке числа 350,001. 350,00110 = 101011110,0000000001000012. Приводим к стандартному виду полученное двоичное число: 1,01011110000000000100001∙(102)1000, q' = 11111112+10002 = 100001112.

Мантисса m = 01011110000000000100001. Знак числа положителен, поэтому s = 0. Окон-

чательно получаем: 01000011101011110000000000100001 или 43AF0021.

		смещенный по-																	мантисса
s				рядок
31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14	13		12	11	10	09	08	07	06	05	04	03	02	01	00
0	1	0	0	0	0	1	1	1	0	1	0	1	1	1	1	0	0	0		0	0	0	0	0	0	0	1	0	0	0	0	1

Обратную задачу получения десятичного числа из чисел, представленных в стандарте IEEE 754, решает следующая формула:

X ( 1) s 2 ( q ' 1 2 7 ) (1 m / 2 2 3 )

(0.0.2)

Если применить эту формулу для вычисления минимального и максимального числа представленного в IEEE 754, то получим следующие результаты:

00 00 00 00h = 5,87747175411144·10-39 (минимальное положительное число)

7f ff ff ffh = 6,80564693277058·1038 (максимальное положительное число)

80 00 00 00h =-5,87747175411144·10-39 (максимальное отрицательное число)

ff ff ff ff h = -6,80564693277058·1038 (минимальное отрицательное число)

Отсюда видно, что невозможно представить число ноль в заданном формате. Поэтому из стандарта сделаны исключения и формула (0.0.2) не применяется в следующих случаях:

1.Число 00000000h считается числом +0. Число 80000000h считается числом -0.

2.Число 800000h считается числом +∞. Число 800000h считается числом -∞.

3.Числа FF(1xxx)XXXXXh не считается числами (NAN), кроме случая п.2. Числа 7F(1xxx)XXXXXh не считается числами (NAN), кроме случая п.2. Число представленное в битах с 0...22 могут быть любым числом кроме 0.

4.(x000)(0000)(0xxx)XXXXXh считаются денормализованными числами, за исключением чисел п. 1.

Стандарт IEEE 754 широко применяется в технике и программировании, несмотря на это, он подвергается эмоциональной и вполне справедливой критике из-за ряда сущест-

венных недостатков (см. напр. http://www.yur.ru/science/computer/IEEE754.htm).

2.4. Кодирование чисел. Операция алгебраического сложения.

Всякое число, прежде чем оно попадает в память компьютера, преобразуется в число в естественной или нормализованной форме. Числа в естественной форме чаще всего дополнительно кодируются. Рассмотрим следующие коды чисел:

прямой код (ПК);

обратный код (ОК);

дополнительный код (ДК).

двоично-десятичный код (BCD или код «8421»).

Простейшим двоичным машинным кодом является прямой код X П К получаемый при

кодировании в числе X только знаковой информации, причем знак + кодируется нулем, а знак – единицей. Если под поле цифр разрядов выделено больше, чем это необходимо для представления числа X, то разряды (цифры) числа X заносятся в разрядную сетку ЭВМ в соответствии со своими весами. Код знака числа практически во всех ЭВМ заносится в старший разряд разрядной сетки. Например, прямой код двоичных чисел

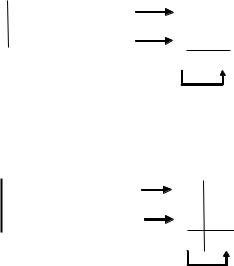
X 1	10 1 12 ,		X 2 1 10 12	для	8-разрядной	ячейки	соответственно	равен
X 1		10 0 0 10 1 1, X 2		0 0 0 0 1 10 1 соответственно.
		П К		П К

Прямой код числа широко используется в ЭВМ при хранении чисел в памяти и выполнении операций умножения. Алгебраическое (с учетом знаков) сложение чисел в прямом коде затруднено, так как требуется выполнить следующие четыре действия:

1.Сравнить знаки слагаемых.

2.Сравнить слагаемые по модулю при неравенстве их знаков.

3.Выполнить сложение модулей слагаемых (при равенстве знаков) или вычитание из большего по модулю меньшего слагаемого (при неравенстве знаков).

4.Присвоить алгебраической сумме знак большего по модулю слагаемого.

Для упрощения алгоритма алгебраического сложения используют несколько усложненное кодирование отрицательных чисел: обратный и дополнительный коды.

Обратный код X О К , также как и в прямой код, для обозначения знака положитель-

ного числа используется бит, равный нулю, и знака отрицательного – единице. Обратный код отрицательного двоичного числа формируется по следующему правилу: в знаковом разряде проставляется единица, а во всех остальных разрядах цифры заменяются на вза-

имно			обратные.	Для рассматриваемых примеров при 6-разрядной сетке:
X 1			1 1 0 1 0 0, X 2	0 0 1 1 0 1 . Алгоритм сложения в обратном коде включает в себя
		О К		О К

два действия:

1.Сложение кодов, включая знаковый разряд.

2.Прибавление переноса к младшему значащему разряду суммы. Пример 1: Вычислить выражение -3(10) -2(10).

Прямой код Обратный код

-3(10)	1	011	1	100
+	+		+
-2(10)	1	010	1	101
			11	001	=1010 бит знака равен 1, следователь-
					но, результат отрицательный.
			перенос		Результат имеет вид в дополни-
					тельном коде: 1101 или -5(10)

Пример 2: Вычислить 7(10) -3(10).

	Прямой код		Обратный код
7(10)	0	111	0	111
+	+		+
-3(10)	1	011	1	100

10 011 =0100 бит знака равен 0, сле-
	довательно, результат
перенос	положительный +4(10).

Работа с обратным кодом вызывает ряд трудностей. В частности, также как и в прямом коде возникают два нуля: +0 и –0, т.е. в прямом коде (в котором представлены положительные числа) имеет место (+0) = 000...0, а в обратном коде (в котором представлены отрицательные числа): (–0) = 111...1.

Кроме того, в операциях сложения и вычитания требуется дополнительная операция по прибавлению бита переноса в младший разряд суммы. Указанные трудности привели к тому, что в современных ЭВМ абсолютное большинство операций с целыми числами выполняется в дополнительном коде.

Дополнительный код сотрицательного числа образуется из обратного кода путем

увеличения X О К		на единицу младшего разряда. При 6 и 8-разрядных сетках дополни-
тельные коды чисел Х1			и Х2 имеют соответственно вид: X 1			1 1 0 1 0 1, X 2	0 0 1 1 0 1 и
					Д К		Д К
X 1	1 1 1 1 0 1 0 1,	X 2	0 0 0 0 1 1 0 1 .
	Д К		Д К

Использование ДК для представления отрицательных чисел устраняет двусмысленное представление нулевого результата, так как –0 исчезает.

В общем случае использованием дополнительного кода для записи отрицательных чисел можно перекрыть диапазон десятичных чисел от –2k-1 до +2k-1–1, где k – число используемых двоичных разрядов, включая знаковый. Так, с помощью одного байта можно представить десятичные числа от 128 до +127, либо только положительные числа от 0 до 255 (здесь под положительными числами понимаются числа без знака).

В ЭВМ используется быстрый способ формирования дополнительного кода. Его суть заключается в следующем. Двоичное число просматривается от младшего разряда к старшему. Пока встречаются нули, их копируют в одноименные разряды результата. Первая встретившаяся единица также копируется в соответствующий разряд, а каждый последующий бит исходного числа заменяется на противоположный (0 – на 1, 1 – на 0).

Пример: Число –44(10) = 10101100 (2) перевести в дополнительный код и обратно.

1	0101		100			ПК	1	0101100	ПК
	инвертируется		сохраняется					инверсия
1	1010		100			ДК	+1	1010011	ОК
								1
	инвертируется		сохраняется				1	1010100	ДК
1	0101		100			ПК
Очевидно, что			X			X	. Приведем также прямой способ перевода числа из
				Д К		Д К	П К

ДК в десятичную систему без использования промежуточного перевода в ПК. Рассмотрим машинное слово произвольной длины (рис. 2.6). При прямом способе перевода десятичное число со знаком формируется как сумма разрядов со своими весами и знаками (старший разряд кодирующий знак имеет отрицательный вес).

Номер разряда		n-1		n-2	n-3	. . .	1	0
		Знак
Вес разряда		-2n-1		2n-2	2n-3		21	20
Пример: Перевести число 1110 из ДК в десятичную систему.
	1 1 1 0(2)		(ДК) = –8+4+2 = –2(10)
Вес	–23 22 21 20

Алгоритм сложения в дополнительном коде включает в себя два действия:

1.Сложение кодов, включая знаковый разряд.

2.Отбрасывание переноса при его возникновении. Пример: Вычислить алгебраическую сумму 58 - 23.