
Практикум 4 (Численные методы) - Численное интегрирование
.pdf
|
|
|
Практикум4 |
. Численноеинтегрирование |
|
|
|
. |
|
|
|
|
||||||||||||||||
|
|
|
Приближенвычислениеопределоетграланного |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||||
|
|
|
|
Формулыпрямоугольников,трапеций,Симпсона |
|
|
|
|
|
|
|
! |
|
|
|
. |
|
|
|
|
|
|
||||||
|
Рассмотримзадавычопределенногоуислеинтегралаия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Аналитическоерешение |
д- |
|||||||||||
даннойзадачи |
|
спомфощьюр |
|
мулыНьютона |
|
|
|
первообразной.О |
|
|
|
|
|
|
|
|
||||||||||||
|
|
-Лейбсводитсякницаахождению |
! |
|
|
|
|
|
|
|
||||||||||||||||||
накод |
лясложнойподынтегральной |
|
|
функции нахождениепервообразнойможбытьдостаточно |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
трудоемкойзада |
|
чей. Болеетого |
|
внекотослучаяперыхвообразной |
|
|
|
|
|
|
|
,представимойаналитическом |
|
|||||||||||||||
виде, |
может несущество |
вать,ноприэтомзначениеопрединтеграласуществуетленногоконечно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
сумм: |
Напомним,чтоопределению |
|
! |
|
определинтеграломнным |
|
|
|
|
|
называетсяпределинтегральных |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
!. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
→! |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
= !"#lim!!! |
! |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Дляп |
риближенноговычислеопределенинтеграламожиявоспользоватьсяноданнымго! |
|
!!! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
определениопуствычпределав,слтостьопределенмниеинтегралможзамнеоыйникоть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о- |
|||||||
ройкон ечнойинтегральнойсуммой |
|
|
|
сдостмшагомлымточно |
|
|
|
|
|
|
|
.Такие |
методы приближенного |
|||||||||||||||
вычисления интеграловполучил |
|
|
и название численноеинтегрирование |
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||||
1. |
Формулапрямоугольников |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Длячисленнинтегрированияспользуемсяго |
|
|
|
|
|
|
|
следующим простымприближением |
|
инте- |
|||||||||||||||||
гральнойсуммы |
|
.Разобьемотрезокинтегрнаравинрованиятервалысые |
|
|
|
|
|
|
|
|
|
|
|
|
|
шагом |
= |
!!!. Врезул ь- |
||||||||||
татеполучимравномернуюсеткуузлов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
! |
|
||||||
|
|
|
! = !, !, … , !| ! = + , = 0, … , ; = |
|
. |
|
|
|
|
|||||||||||||||||||
|
Далее вычислимзн |
аченияподынтегфункциивсередиаинтждоголь.Знаеойрвала |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чение |
|||||||||||
искомого интегвыбиррапривнымла( ется |
|
|
|
|
|
ближенно)суммевычислезначефунныхкцииий |
|
|
|
|
|
|
|
|
|
|
вс |
е- |
||||||||||
рединеинтервалов,умноженных |
|
|
надлинуинтерваларазбиения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
! |
≈ |
! |
|
!!! + ! |
|
= ! |
|
|
!!! + ! |
|
= |
|
− |
! |
|
!!! + ! |
. |
|
||||||||
|
Данная! |
|
|
|
|
|
||||||||||||||||||||||
|
формулаполучиланазвание!!! |
2 |
|
|
формулапрямоугольников!!! 2 |
|
|
. |
!!! |
|
|
|
2 |
|
|
|
||||||||||||
|
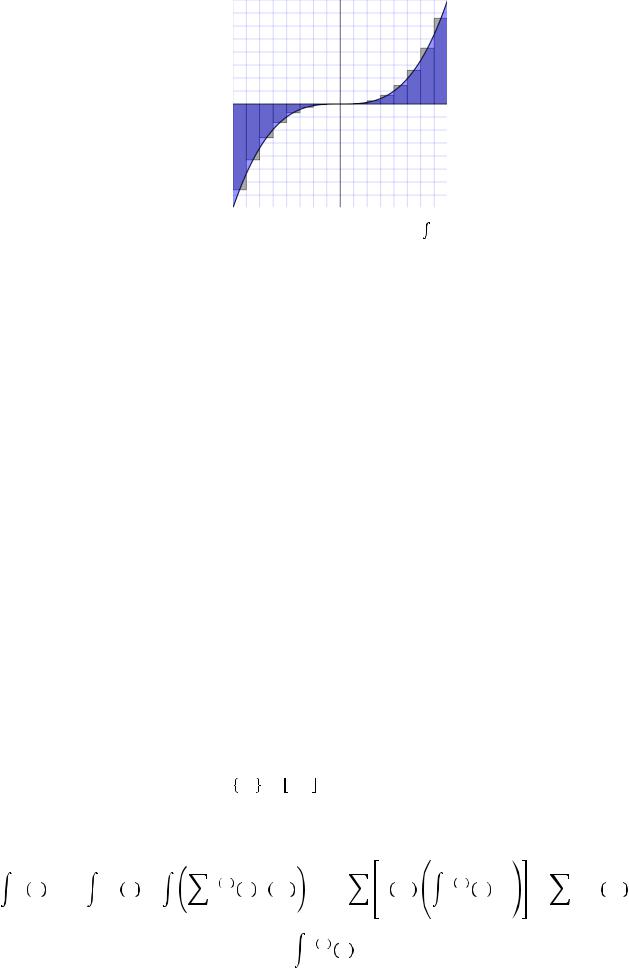
Геометрическпрямоугольниковинтерформулыетацприведенарису кеа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вверхусл |
е- |
|||||
дующейстраницы |
|
. Напомним,чтозначениеопрединтегналенногоотчислрезкеалар внно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
площади криволинейнойтрапеции |
|
, ограничеподынтегральнойфу,осьюкцабсциссв |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р- |
|||||||||||
тикальнпрямнаконцахымиотрезковинтегрирования. |
|
|
|
|
|
|
|
|
|
|
Прииспользованииформулыпрям |
|
|
|
о- |
|||||||||||||
угольниковподынтегральнаякриваякаждомучасткеза константойен,.е.вместоетсяплощади |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
трапециииспользу |
|
етсяплощадьпрямоугольника. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Погрешностьвычисленийформулепрямоугольниковопредеразносплощадейяетьюся |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е- |
|||||
рыхисветло |
-синихфрагментовнарисунке.Чемближефорнамаивойк изждомучастковпр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
я- |
|||||||
мойлинии,темменьшеданнаяразностьи,соответстве |
|
|
|
|
|
|
|
|
нно,точнеерезультатвычисления. |
|
|
|
|
|
|
|
|
|
||||||||||
|
Еслифункцияявляетсякусочно |
|
|
|
-постояннойиликусочно |
|
|
|
|
|
-линейной,тоформулапрямоугол |
|
|
|
ь- |
|||||||||||||
никовбудетдаватьточноезначениеинтегралапри(условразрывовпадеиифуинееприякции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о- |
|||||
изводнойсточкамиразбиения)В.общемслуча |
|
|
|
|
|
еточностьформулыпрямоугольниковжноценить |
|
|
|
|
|
|
|
|
|
|||||||||||||
поформуле: |
|
|
|
|
|
≤ max!,! | "( )| |
− |
|
! |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пример 1. Рассчитчисленныезнинтегралачениять |
= ! |
|
! |
|
спомфопрщьюрмулы |
я- |
|
! |
|
|
|||||
моугольн.Шразбвыбратьиравныменияков0Рассчи.1. |
(I0= 1/3) значенийинтеграла. |
татьпогрешностьвычислениякакра |
з- |
||||
ностьчисленточного |
|
|
|
|
|
|
|
>>a=0; b=1; h=0.1;
>>x=a:h:b;
>> n=length(x)-1; |
%Либо: n=(b |
-a)/h; |
|
>> |
x_m=(x(1:n)+x(2:n+1))/2; |
%Координатысередининтервалов |
|
>> |
f=x_m.^2; |
%Значениефункцсерединахв нтервалов |
|
>>I=sum(f)*h
I =
0.3325
>>I0=1/3;
>>dI=I-I0
dI = -8.3333e-04
Упражнение 1. Длявыполненияупражвыбратьениятегралсоответствииномером |
|
|
|
|||
компьютерасписок( вариантовпривед |
|
енвконцеработы). |
|
|
|
|
1) Вычислитьзначенияинтеграла |
спомфопрямоугольщьюрмулыдлятрехзначениковй |
|
|
|
||
количестваинтерваловразбиения( |
|
n = 10, 100 и1000). Сравнитьпо |
лученныезначения |
. |
|
|
2)Рассчитатьпогрешностьвычислениякакразностьточного |
|
|
гозначенийинтегр |
а- |
||
лапослед( колонкатаблицы).яя |
|
|
|
|
|
|
Примечание: |
Рекомендудляэконовререализоватьмтсяииениформулупрямоугольников |
|
|
|
||
видефайла |
-функции. |
|
|
|
|
|
2. Квадратурныеформулынаосновеинтерполяции.
Пустьзаданасеткаузлов |
|
|
! = |
! |
, , = 0,1, … , |
,необязравномернаятельно. |
|
поданной |
||||
ставимподынтегральнуюфункцию |
|
|
( ) |
интерполяционнымполиномомЛагранжа |
|
!( ) |
|
|||||
системеузлов. |
Значеискомоинтиебудетпгроиближенала |
|
|
равнозначениюинтегралаотпол |
и- |
|||||||
номаЛагранжа: |
|
! |
! |
! |
|
|
|
|
! |
! |
! |
|
! |
|
!! |
! |
= |
|
|||||||
≈ |
! = |
! |
!!! |
! |
!! |
= ! ! , |
||||||
! |
|
! |
|
|
! |
!! |
!!! |
! |
!!! |
|
||
|
|
|
|
|
|
|
! = ! |
. |
|
|
|
|
2
Обратитевнимание,чток эффициенты |
|
называется |
зависят олькоотпорядкамногочлена |
инезависят |
|
|||||
отинтегрируемойфункции.Такая |
|
|
квадратурнойформулой |
|
n-гопорядка . |
|
||||
Точностьэтогометодавобщемслучаежноценитькак |
|
ормула |
! |
|
|
|
!!! |
. Приповышенииколич |
е- |
|
|
|
|
|
|
||||||
стваузлов |
и,соответственно,порядка |
|
формулы,точзначительноостьвозрастает, приэтакжеом |
|
|
|
||||
сильнорастетсл реализацжностьсчетувелколичествачениякоэффициентовформулы.П |
|
|
|
|
|
|
|
о- |
||
этомуобычнонапрактикевместоповышенияметодарядкасувелчиузсчениемиспользаов |
|
|
|
|
|
|
|
у- |
||
ютальтернатив ныйподход: |
областьинтегриразбинаавныеоваподобластиаетснебольшимия |
|
|
|
|
|
||||
числомузлп дынтегральнаявфункциязаменяетсинтерполяционнымполиномомнизкойстеп |
|
|
|
|
|
|
|
е- |
||
нидлякаждойподобласти. |
|
|
|
|
|
|
|
|
|
|
Формулы,получаемыетакимспособом,называют |
|
|
|
|
|
обобщеннымиквад |
ратурнымиформулами |
|
||
n-гопорядка |
или формуламиНьютона |
-Котеса. |
|
|
|
|
|
|
||
Напрактикеш рокоспользуютсятривформулдаНьютона |
|
|
|
|
|
|
-Котеса:ужеизвестнаянам |
|
||
формулапрямоугольниковформула( 0 |
|
-гопорядка),формула |
|
трапеций(1 |
-гопорядка)иформула |
|
||||
Симпсона(2 |
-гопоряд ка)Формулы. болеевыспорядкиспользуютсякихвоченьвэкзотич |
|
|
|
|
|
|
е- |
||
скихслучаях. |
|
|
|
|
|
|
|
|
|
|
Формулатрапецийиспользуетдляпредставленияфункциикусочно
! |
! !!! |
+ ! |
|
! |
= !!! |
2 |
= |
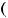
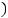
2
!!! |
|
-линейнуюинтерполяцию: |
||
|
− |
|
||
+ !!! ! + |
2 |
, = |
|
. |
Фотрапециймулаимееттакожепорядок |
|
точности, |
какиформулапрямоугольников: |
|
||||||
|
|
≤ max!,! |
| "( )| |
− |
!. |
|
|
|
|
|
Новотличи |
е отформулыпрямоугольников,котораяиспользовалазначенияфункциисер |
|
12 |
|
|
|
|
|
е- |
|
динтервалов,формулатрапзнанияецийбуетфункциитольковузлахразбиения.Вомногих |
|
|
|
= |
|
! |
|
|
||
случаяхэтооказываесущеспреимуществомсявенным. |
|
|
|
! |
|
|
||||
Пример 2. Рассчитчисленныезнинтегралачениять |
|
|
|
спомфотрапщьюрмулы |
е- |
|||||
ций.Шразбиенияг |
выбратьравным0Рассчитать.1.погрешностьвычислениякакразность |
|
|
! |
|
н- |
||||
ногоиточного( |
I0 =значений1/3)интеграла |
. |
|
|
|
|
|
|
|
|
>>a=0; b=1; h=0.1;
>>x=a:h:b;
>>n=length(x)-1;
>> f=x.^2; |
%Значениефункцвычвисходныхсляетсяузлах |
>>I=h*(f(1)/2 + sum(f(2:n)) + f(n+1)/2)
I =
0.3350
>>dI=I-1/3
dI = |
|
|
0.0017 |
|
|
ДляпостроенияформулыСимпсона |
(ееещеназываютформулойпарабол) |
наборузловсетки |
разбиваютнатройкипопринципу,указрисункеаниженому.Обратитевнимание,чтодляприм |
n обязателдолжнобытчет.ь ымо |
е- |
нимформулыСимпсонастичинтерваловслоразбиения |
|
Длякаждойпоследтрузловстроятйвательки адратичнуютерполяциюой |
(наборпар |
а- |
бол),котораядалееисподпредсляьзуеподынтегральнойавлесяфункции: ия |
|
|
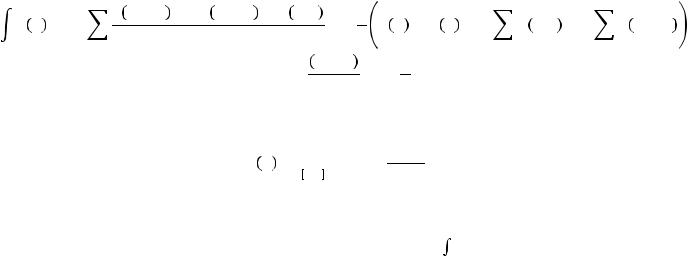
! |
! |
+ 4 !!!! + !! |
|
|
|
|
|
|
|
|
|
|
||
! !!!! |
|
|
|
|
|
|
|
|
|
|||||
! |
= !!! |
3 |
|
|
= |
3 |
+ |
|||||||
|
|
|
|
− |
|
|
|
|
|
|
|
|||
|
ФормулаСимпсоимеетточнадвапорядкаостьвышеформулпрямоугольниковтра |
= |
|
|
|
, = |
2 |
. |
|
|
|
|||
ций: |
|
≤ max!,! | |
!" |
( )| |
− |
|
! |
. |
||||||
|
|
|||||||||||||
|
|
|
180 |
|
||||||||||
+ 2 |
!!! |
+ 4 |
! |
!!! !! |
!!! !!!! , |
пе-
Обратитевнимание,чтодляполиномовпорядкаили3 формулажедаетточныйрезультат
(произвчетвепоуднаяртакихядкатогофункцийравна0). |
= |
! |
! |
|
|
|
Пример 3.Рассчитчисленныезнинтегралачениять |
спомфощьюрмулы |
Симп- |
||||
сона.Шразбиениягвыбратьравным0Рассчитать.1.погрешностьвычислениякакразность |
! |
|
н- |
|||
ногоиточного( |
I0 = 1/5)значенийинтеграла. |
|
|
|
|
|
>>a=0; b=1; h=0.1;
>>x=a:h:b;
>>n=length(x)-1;
>>f=x.^4;
%Призаписи |
формулынеобходучестьсдвигиндексациимомассивовдля |
MATLAB |
>>I=h/3*(f(1) + f(n+1) + 2*sum(f(3:2:n-1)) + 4*sum(f(2:2:n)))
I =
0.200013333333333
>>dI=I-1/5
dI = |
|
|
|
1.333333333333742e-05 |
|
|
|
Упражнение 2. Длявыполненияупражвыбратьениятегралсо |
|
ответствииномером |
|
компьютерасписок( вариантовприведенконцеработы). |
|
|
|
1)ВычислитьзначенияинтегралапомфотрапецийщьюмулСимпсонадлятрехзначений |
|
|
|
количестваинтерваловразбиения( |
n = 10, 100 и1000). |
|
|
2)Рассчитатьпогрешностьвычисленияка |
кразностьчисленточзначенийинтегрого |
а- |
|
лапослед( колонкатаблицы).яя |
|
|
|
3)Сравнить |
полученные результаты срезультатапражненияфор1 (прямоугольнула |
и- |
|
ков). |
|
|
|
Примечание: |
Рекомендудляэконовререализмтсяиспениметользуемыеватьвид |
|
|
файла-функции. |
|
|
|
3. ПравилаРунге
Оценкиточности,которыеприводилисьпредыдущихчастяхработы, |
|
|
предполагают, |
что |
||
возможнооценитьвеличинусоответствующихпроизводныподынтегральнойфункции. |
|
|
|
Однаков |
||
реальныхзадт окч ях |
цен,какправило,невозможна |
литрудоемка.Сущесальтернативует |
|
|
в- |
|
ныйспосоценкипогрешбинтегрирравностисеткикоторы, ваниямернойнетребуетпрои |
|
|
|
|
з- |
|
водных. |
|
|
|
|
|
|
Предположмыпровелрасчетинтегнанекотороймравномласеткешагомрной |
|
|
h, полу- |
|||
чивзначение |
|
расчетэтогоинпотойеграла |
-жеквадратурнойформуле, на |
|
|
у- |
гойравномсеткешагомрной !. Далеепроведем |
rh (r > 1). Полузначениеинтегралаимравное |
|
. Пусть известно, |
|||
чтометодинтегриимеетпоточностирядокования |
|
|
прямоугольниковтра |
|
пе- |
|
|
|
|
p (p = 2 дляформул |
!! |
|
|
4
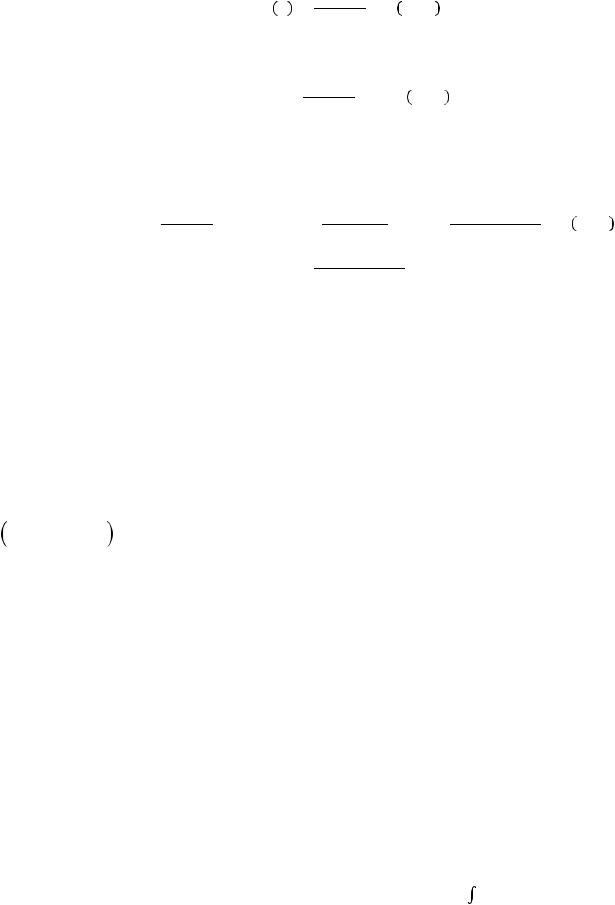
ций, p =дляформулы4 Симпс),тогдадлягрешностиназначения |
|
|
|
! − !! |
|
!!! |
! |
справоц(енкадлива |
первая |
|
формулаРунге |
): |
|
|
|
|
|
|
|||
Изэтойоценполучитьлегкоформулудлявычислзначенияболеточе искомого ! |
|
= |
! − 1 |
+ |
|
. |
|
|
||
интеграла( |
вторуюформулуРунге |
): |
|
|
|
|
|
|
|
|
≈ ! + !!− !! , = !!! .
− 1
ВтораяформулаРунгепозволяетначиповыситьочносельнорасчетаинбувьгралаз |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, , |
! |
|
|
е- |
||||||
личенразмерасеткисменыяметодаинтег.Кртироэтуформулугмеможнования |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
использо- |
|||||||
ватьрекуррентно.На,проводимимеррасчетинтеграланатрс схшагомткх |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!,!! − !!,!!! |
.Повторой |
|||||||||
формулеРунгепровуторасчетачнениедимпоследующейсхеме: |
! − !! |
|
|
|
|
|
|
|
!! − !!! |
|
|
|
|
|
|
||||||||||
!,!! = ! + |
, !!,! |
! |
! = !! + |
|
, !,!! = |
+ |
!!! |
, |
|
|
|||||||||||||||
! − 1 |
|
! − 1 |
!!! − 1 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
! |
|
|
|
!,!! − !!,!!! |
|
|
!!! |
|
|
|
|
|
|
|
||||||
|
|
|
!,!!,! |
|
! |
|
!,!! |
+ |
|
|
!!! |
− 1 |
|
, = ( |
|
). |
|
ующейсетке, |
|
||||||
|
одинарныминдексомобозначаютрезультатрасчесоо ветств |
|
|
|
|
|
|
||||||||||||||||||
Значения I с |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|||||||||
двойныминдексом |
– результатоднокрауточнениягопов формулеоройРунге, |
|
|
|
|
|
|
|
|
|
|
|
стройныминде |
к- |
|||||||||||
сом - резульдвукраточ. ненияого |
|
|
|
|
|
|
Оценкаточностип следнократногоуточнения |
|
|
|
|
|
|
|
!,!! |
полу- |
|||||||||
ченапопервойфо |
рмулеРунгесучетомповышенного |
|
|
|
|
порядкаточности |
|
. |
|
|
|
|
|
||||||||||||
Приналичиирезультарасчетаов начетырехсеткахподобноерекурреточможнтеноие делатьтрехкраподум( как)итнымак.Такимйтелеобрамыожемзомначительносократить числоточекнеобходдлявычимыхсления интеграласвысоко йточностью.
Упражнение 3. Длявыполненияупражвыбратьениятегралсоответствииномером компьютерасписок( вариантовприведенконцеработы).
|
1)ВычислитьинтегпофоСимпсонаралмуледлядвухзначенийинтерваловразбиения |
|
|
|
|
|
|
|
||||
(n = 10, n = 20)Получи. |
тьоценкуточз аченияосинтеграладля |
|
|
|
|
|
n = 20 попервойформулеРунге |
|||||
|
= |
!!"!!!" |
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
|
|
|
||
!",!" |
|
|
|
|
|
|
|
|
|
|
|
|
|
2) По! в!!ычислениеторитьинтегралапоследовувелизначчетислонтерваловльноваяие |
|
|
|
|
|
|
|
||||
Рунге (т.е.получить |
|
= 40,80,160, … |
)икаждыйраз |
|
|
оцениваяточностьпопервойформуле |
|
|||||
разбивраза2т.е(.дляния |
|
|
|
|
|
|
||||||
|
|
последовательностьошибок |
|
!",!" |
, |
!",!" |
ит.д.) .Определитьзначение |
n прик о- |
||||
торомточностьвычисления |
|
|
становитсяменьше |
|
|
|
о- |
|||||
|
|
|
|
|
|
10!!" |
. Проверправоценкиточнлтьность |
|||||
стидляэт |
|
ого n исптознльзуячное |
!/!,! ачениеинтеграла. |
|
|
|
||||||
|
3) Используя значе,полученныешагахияи1ирек2, рреточзначенийпотеноеи |
|
|
|
|
|
|
|||||
второйформулеРунге,опр делить |
|
значение n прикоточностьвычисленияром |
примаксимально |
|||||||||
возможномчислеуточнений |
|
|
становитсяменьше |
!!" |
(этозначениебудетменьшечемполученное |
|
||||||
навторомшаге) |
|
. |
|
|
|
10 |
|
|
|
|
|
|
4. Реализациясреднеквадратичногоприближенияфункциями |
|
|
|
|
|
MATLAB |
|||
|
Впакете |
MATLAB реализованафункция |
интегрированияпоформулеСимпсона |
|
|
.Д лявызова |
|||
даннойфункциииспользуетсякоманд |
а quad(fun, a, b, tol), параметкоторойами |
|
являютсяфункция |
||||||
fun ввидестрокиилиуказателянафункцию,гра ицытегрирования |
|
|
|
a, b ижелаемаяотносительная |
|||||
точностьвычислений |
tol (последнийпараметржнопус, этиоитьмчностьпоумолчанию |
|
|
|
|
||||
будетр |
авна |
|
!!). |
|
|
|
|
|
|
|
Пример 4Рассчит. численныезнинтегралачениять |
|
|
|
|
|
спомощьювстроенной |
||
|
|
10 |
|
|
10!!, 10!!). |
= |
!! ! |
|
|
функции MATLAB длядвухзначеточ(нийости |
|
|
|||||||

>>I=quad(@(x)x.^7,0,1,1e-4)
I =
0.125005691150698
>>I=quad(@(x)x.^7,0,1,1e-8)
I =
0.125000000623625
Упражнение 4. Длявыполненияупражвыбратьениятегралсоответствииномером компьютерасписок( вариантовприведенконцеработы).
1)Вычислитьзначенияинтеграла |
!! |
|
!!"). |
спомощьювстроеннойфункции |
MATLAB длятрехзнач |
е- |
|||
нийточности( |
10 |
!! |
, 10 |
, 10 |
|
|
|
||
2) |
|
|
|
со значениями, |
полвученнымипражнениях12. |
|
|||
Сравнить |
сточнымзначением |
|
|||||||
Задлявыполненияаниялабораторнойработы.
Номервариантасоответствукомпьютерапоследнцифреномера.й
№ |
|
|
f(x) |
|
|
|
a |
|
b |
|
|
|
|
I0 |
||||||||
вар-та |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
! |
) |
|
|
|
|
|
|
+ ln 2 − 2 |
||||||||||
1 |
|
|
|
|
|
0 |
1 |
|
|
|||||||||||||
|
ln(1 + |
|
|
|
|
|
2 |
|||||||||||||||
2 |
! |
1 + ! |
|
0 |
2 |
|
9 |
5 |
− |
ln |
5 |
+ 2 |
||||||||||
3 |
|
sin 2 |
|
|
0 |
|
|
|
4 |
|
8 |
|
||||||||||
4 |
1 + sin ( ) |
0 |
2 |
|
|
|
2 − ln 4 |
|||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||
5 |
|
1 + cos! |
|
-1 |
|
20 |
|
|
|
|
|
|||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|||||
6 |
|
! |
+ 2 + 2 |
0 |
2 |
|
|
ln 1 + 2 |
||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
4 − ! |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
7 |
|
cos ln |
|
|
1 |
|
e |
|
|
sin 1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
8 |
|
|
sin |
|
|
|
0 |
|
|
|
|
− 2 |
||||||||||
|
|
1 + sin |
|
|
|
|
||||||||||||||||
9 |
|
sin |
! |
|
|
0 |
|
|
|
1 − cos ! |
||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||
0 |
|
! sin |
|
|
0 |
|
|
|
|
! − 4 |
||||||||||||
6
