Практикум 6 (Численные методы) - Задача Коши для систем ОДУ
.pdf
|
|
|
|
Практикум6 |
|
. ЗадачаКошидлясистемОДУ |
|
|
|
|
|
. |
|
|
|
|
|||||||||||
|
|
МетодЭйлярешенияразКошидачи |
|
|
|
|
|
|
|
|
|
|
. МетодыРунге |
|
-Кутты. |
|
|
|
|||||||||
Вэтойлабораторнойработемырассмотримнекоторыеприближенныеметодышениязад |
|
|
|
|
|
|
|
|
|
|
|
|
! |
= , |
|
а- |
|||||||||||
чиКоши,состоящейвотысканиирешения |
|
|
|
|
|
|
|
|
|
|
диффеуравненияенциального |
|
|
,удовл е- |
|||||||||||||
творяющегозаданномуначальномуусловию |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||||
ЗадачуприближеннрешениязадачиКошибудемнимкакгозадпостроенияатьчуназ |
|
|
|
! = ! |
|
|
|
|
|
|
|
|
|
|
а- |
||||||||||||
данномотрезке |
|
|
|
|
функции |
|
|
,котоблизка«»решениюая |
≤ ≤ |
|
|
|
задачиКошисзаданной |
|
|
||||||||||||
|
чтоысле |
|
|
| − | ≤ |
. |
|
|
|
|
|
|
|
|
||||||||||||||
точностью втомс , |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1. Метод Эйлера. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Рассмотрим задачуКошидляуравнения |
|
|
|
|
1-гопорядка: |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= , , |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Будемискатьчисленнрешеуравненияоиетрезке |
.Заменпров |
|
|
|
|
! = . |
= |
. Зададим наэтомотрезсетку |
|
|
|||||||||||||||||
{ !, = 0,1, … , } |
|
|
|
|
|
|
! < ! < < ! |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
, такимобразом,чтобы |
|
|
|
|
|
|
|
|
|
|
|
|
|
Введемобозндляшсеткиачениега |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. !, |
|
|
|
|
|
|
|
|
|||
! = !!! − !, = 0, … , − 1 |
|
|
|
уравнениизводнуюправойразн,получимстью |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
!!! − ! |
= !, ! |
= !, = 0,1, … , − 1. |
|
|
|
|
|
|
|
|||||||||||||
Известно,что |
|
! = ! |
|
! |
.Откуда |
можнонайти |
|
всеостальныезначения |
|
|
|
! |
по рекуррент- |
||||||||||||||
ной формуле: |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Данметоднахождрешенияыйчисленназываетсяного |
|
|
!!! = ! + ! !, = 0,1, … , − 1. |
методомЭйлера |
|
|
(или |
методом |
|||||||||||||||||||
ломаных)Схемы. ,вкоторыхзначениефункцииявноыражчерезуженаетсяйденныезнач |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ения, |
|||||||||
называютсяявными,иначе |
|
|
|
– неявны.Такиобразом,схемаЭйлераиявляетсяявной.Оценкап |
|
|
|
|
|
|
|
|
|
|
|
о- |
|||||||||||
грешносдляданногомедаетодаи |
|
|
|
|
|
|
|
|
max ! |
,чтопредполагаетмалыйшагсеткидляполучения |
|
|
|
|
|
|
|
||||||||||
удовлетворрешен. ительногоя |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Нак изждомотрезков |
|
|
[ !, !!!] |
полученноерешбудетпредсниесобойотрезокавлятьпр |
|
|
|
|
|
|
|
я- |
|||||||||||||||
мой,провчерезточкуднной |
|
|
|
|
|
|
|
|
суглковымэффициентом |
|
( !, !) |
.Такаягеометрическая |
|
н- |
|||||||||||||
терпретациярешения |
|
|
|
названиемметод( одаломанных). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
объяснявторо |
|
!, ! |
|
|
|
|
|
|
|
|
|
|
|
|
[0, 1] |
|
|||||||||
Пример 1. Найдитечисленное |
решениеследующей |
|
задачиКоши |
наотрезке |
|
методом |
|||||||||||||||||||||
Эйлерана(равномсеткерной |
|
|
|
|
сшагом |
|
= 0.1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
)исравегонитеалитическим: |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! = !, |
|
|
|
|
|
|
|
|
|
|
|
||
Реализуемме |
тодЭйлераввидефайла |
|
|
|
|
|
|
- |
0 = 1. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
функции: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
function [yy,xx]=euler(f,x0,y0,xe,h) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
xx = x0:h:xe; |
|
|
|
|
|
|
|
%значениякоординатхдлрасчета |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
yy = zeros(length(y0),length(xx)); |
|
%выделпамдлязначенийемтьфункции |
|
|
|
|
|
|
|
||||||||||||||||
|
|
yy(:,1) = y0; |
|
|
|
|
|
|
|
%начальноезначение |
|
|
y |
|
|
|
|
|
|
|
|||||||
|
|
for i=1:length(xx)-1 |
|
|
|
%последоватвычислзначенийльноение |
|
|
|
|
|
|
|
|
|
||||||||||||
yy(:,i+1) = yy(:,i) + h*f(xx(i),yy(:,i));
end
end
Такженампонадобитсявспомогательныйфайлдляфункцииправойчастиуравнения:
function f = f(x,y)
f=x.^2;
end
СпомощьюсоздафунайдемныхкцийрешениезадачиКоши:
>> [y,x]=euler(@f,0,1,1,0.1) y =
|
|
|
1.0000 |
1.0000 |
1.0010 |
1.0050 |
1.0140 |
1.0300 |
1.0550 |
1.0910 |
||
1.1400 |
|
1.2040 |
1.2850 |
|
|
|
|
|
|
|
||
|
x = |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0 |
0.1000 |
0.2000 |
0.3000 |
0.4000 |
0.5000 |
0.6000 |
0.7000 |
|
0.8000 |
|
0.9000 |
1.0000 |
|
|
|
|
|
|
|
||
|
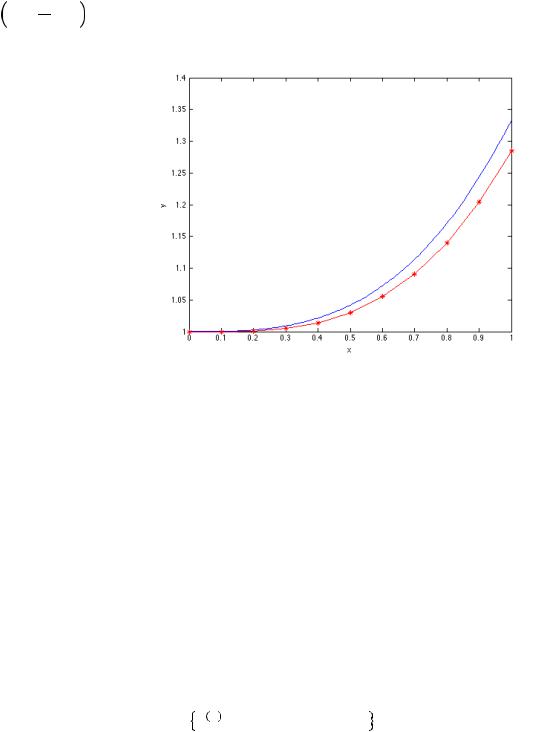
Отобразимнаодномграфикепол |
|
ученнрешениеточное,найденноеаналитичние |
|
|
|
е- |
|||||
ски |
= |
! |
+ 1 |
.Результатпредставленнаследующемри (икриваяяяке |
|
|
|
– аналитическоер |
е- |
|||
|
!! |
|
|
|
|
|||||||
шение,краснломсимволаминная |
|
– приближенноерешение). |
|
|
|
|
|
|||||
Упражнение 1. Длявыполненияупр |
|
|
ажнениявыбрать |
задачуКоши |
дляуравнения1 |
-гопоря |
д- |
|||||
ка всоответствииномеромкомпьютерасписок( вариантовприведенконцеработы). |
|
|
|
[0,1] |
|
|
|
|
|
|
||
сшагом1) Найти . |
|
|
|
|
методомЭйлера |
,используяравномернуюсетку |
|
|
||||
решениезадотрезкеачи |
|
|
|
|
|
|
|
|
||||
Найти ошибвычислений,каку |
|
|
|
разностьмежду |
|
точнымрешениемзадачи( ожнонайти |
|
|
|
|||
2) = 0.1 |
|
|
|
|
|
|
|
|
||||
бумажкеиливс мвольномвидеспомощьюфункции |
|
|
|
|
|
|
dsolve) и полученным численнымрешениемв |
|
|
|||
каждойточкесетки.Определитьпогрешнос |
|
|
|
|
тьрешения,какмаксимуммодуля |
|
|
ошибкивычислений |
. |
|||
3) Пострографитьки |
тоичногоислерешен(одноманогорисунке)графикя |
|
|
|
|
|
ошибки |
|||||
вычислна(отдрисункельномний). |
|
|
|
|
|
|
|
|
|
|
|
|
4)Повторитьрешениезадшагаляачисетки |
|
|
|
|
|
|
|
|
построеннымвпункте3, |
|
|
|
добавитьграфновогоч ксленнрешенияграфикогоответствующейему |
|
|
|
|
|
= 0.05.Кграфикам, |
ошибки. |
|
|
|||
2. Решениеуравнений |
p-гопорядкаисистемОДУ |
|
|
|
. |
|
|
|
||||
Рассмотримобыкновенноедифференциальноеуравнение |
|
|
(!) |
! |
|
|
(!!!) |
p-гопорядка: |
|
|
||
|
|
! |
|
|
|
). |
|
|
|
|||
Путзаменывведения |
|
|
= ( , |
, ", … , , |
|
|
е- |
|||||
ме дифференциальных |
уравненийпервогопорядка: |
= !, = 1, … , − 1 |
данноеуравнеможсвестиксистниео |
|
|
|
||||||
|
|
|
|
|
|
|
||||||
′ = !,
|
|
|
!! |
= !, |
|
|
|
|
|
! |
… |
|
|
|
|
!!!! |
!!! |
= !!!, |
|
|
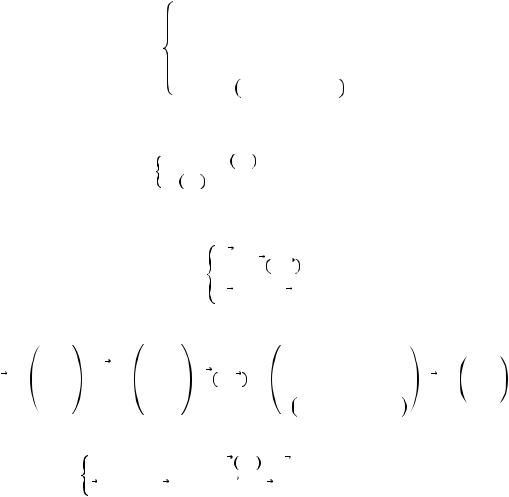
Дляполученединстврешизсистемыяенужноияогоалжить |
= , , !, … !!! . |
p дополнительныхусл |
о- |
|||
вийнафункции |
!( ).ДлязадачиКошиданныеуслозадаютсяводнойияточке: |
! |
= !, |
|
|
|
ДлянахождерешенияполученнойзадачиКошияможетбытьприменен |
! ! |
= !, = 1, … , − 1. |
методЭйлера, |
с- |
||
смотренныйранее. |
Дляэтогопредстполученнуюзавдачувекторномимвиде |
|
|
|
|
|
= , ,
!
= ,
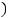введяобозначения :
|
|
|
|
|
|
! |
|
! |
|
! |
||
|
! |
|
|
|
|
! |
|
… |
|
|||
|
|
|
! |
|
|
|
… |
|||||
= |
|
, |
= |
|
, , = |
!!! |
, = |
|
||||
… |
|
|
… |
|
|
!!! . |
||||||
|
!!! |
|
|
|
! |
|
|
, , , … , |
|
|||
|
|
|
|
!!! |
|
|
|
|||||
|
|
|
|
|
|
! |
!!! |
|
|
|||
ВданныхобозначенияхформулыметодаЭйлерамогутбытьпредставленывиде:
|
|
|
|
( |
|
|
! = , |
|
|
|
|
|
Обратитевнима,чтофудлянмиекция |
) = ( ) + ( , ( )), = 0,1, … , − 1. |
|
||||||||||
|
|
|
|
!!! |
|
! |
!етодаЭйлера,описанная! впр1,! мерезначальнобыла |
|
|
|||
рассчитанаработупеременными |
|
|
y, y0, заданнымиввидевектора |
|
|
-столбца.Вноситьдополн |
и- |
|||||
тельныхизменевэтуфудлянрешениякцийс уравнюстемнетре.Досбуенийлишьтаточнося |
|
|
|
|
|
|
|
|
||||
правильнозад ть |
|
|
метрыиреализоввычислениеправой.тьсти |
|
|
|
|
|
|
|||
Упражнение 2. ДлявыполненияупражнениявыбрзадКошидлятьчууравнения2 |
|
|
|
-гопоря |
д- |
|||||||
кавсоответствииномеромкомпьютерасписок( вариантовприведенконцеработы). |
|
|
[0,1] |
|
|
|
|
|
||||
Найтирешениезадотрезкеачи |
|
|
|
методомЭйлера,используяравномернуюсетку |
|
|||||||
порядка. |
= 0.1 |
ипредварительнопреобраззад Кдачудлясистемышивавуравнений1 |
|
|
|
|
-го |
|||||
сшагом1) |
|
|
|
|
|
|
||||||
2)Найтиошибвычислений,кразностьакумеждуточнымрешениемзадачи( ожнонайти |
|
|
dsolve) иполученнымчисленнымрешениемв |
|
||||||||
бумажкеиливс мвольном |
|
|
видеспомощьюфункции |
|
|
|||||||
каждойточкесетки.Определитьпогреш,какмаксимуменияностьмодуляошибкивычислений. |
|
|
|
|
|
|
|
|
||||
3)Пострграфоичногоислетькирешен(одноманогорисунке)графяошибки |
|
|
= 0.05 |
|
|
|
||||||
вычисленийна( |
отдельномрисунке). |
|
|
|
|
|
|
|||||
4)Повторитьрешениезадшагаляачисетки |
|
|
|
|
.Кграфикам,построеннымвпункте3, |
|
||||||
добавитьграфновогоч ксленнрешенияграфикогоответствующейемуошибки. |
|
|
|
|
|
|
||||||
3. МетодыРунге -Кутты. |
|
|
|
= ( ),т.е.методЭйлераимп ет |
|
|||||||
Дляпогрешности |
методаЭйлера |
справоценкадлива |
р- |
|||||||||
выйпорядокточности. |
|
|
Этоознача,чтодляуменьшпогртвычешностия100разсленийшаг |
|
|
|||||||
четнеобходимотакжеуменьшитьв100раз.Дляболпрактическихшинзадач, ожалениютва, |
|
|
|
|
|
|
|
|
||||
такойнизкийпорядокточностине |
|
|
|
статочен. |
|
|
|
|
|
|||
Длярешенияпостзасдачивленнойболеевысп рядкпридуманоточнкимбылостиц |
|
|
|
|
|
|
е- |
|||||
лоесемействомет,п лучившеедовназваниметодыРунге |
|
|
|
|
|
-Кутты. |
Наиболеепопулярныйизэтих |
|
||||
методов – методРунге |
-Кутты4 |
-гопорядкаточности,которыймырассмотрим |
|
|
далее.Такженапра |
к- |
тикечастоприменяютметод2 |
|
-гопорядкаиужезнакомыйнамметодЭйлераметод( Рунге |
|
|
-Кутты1 |
- |
гопорядка)В.литературезрабметРунгеотаныды |
|
|
-Куттыдо8 |
-гопорядкаточности |
включительно, |
|
но практическогораспространенияполучи |
ли. |
|
|
|
|
|
ДляпоискарешениязадачиКошиспомощьюетодовРунге |
|
|
-Куттывобластивводра тся |
в- |
||
номернаясеткаизнфункцчениявычпоследовательноисляютсяи,начинаяизвестн |
|
! |
|
огозначенияв |
|
|
точке !. Вобщемвидеформуладлявычисленияновогозначенияфункцииза |
|
даетсякак: |
|
|||
|
|
!!! = ! + |
! ! , |
|
|
|
|
|
|
!!! |
|
|
|
! = 
!, !
,
! = 
! + ! , ! + !" !
,
…
! = ( ! + ! , ! + !! ! + !! ! + + !,!!! !!!).
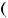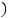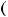Каждыйконкрметодс мействатныйРунге |
-Куттыопредечиспроляемэежуточныхся |
|
|
а- |
||||||||
повстадий( ) |
s ификсированнымизначениямикоэффиц ентов |
|
|
|
|
|
|
!", !, !. Значениякоэффициентов |
|
|||
подбираютсятакимобразаданном,чтобыприпорядкеточностиислотребуемыхстадийбыло |
|
|
|
|
|
|
|
|
||||
минимальным. |
|
|
|
|
|
|
|
|
|
|
|
|
Вчастности,методЭйлераимеетоднустадиюкоэффициент |
|
|
|
|
|
|
|
. Для достижениявтор |
о- |
|||
гопорядкаточнотребуетсядвестадии( |
исподэтогользуемыея |
|
значениякоэффициентовможно |
|
|
|||||||
|
! = 1 |
|
|
|
||||||||
легко найтивлитературе). |
|
|
|
|
|
|
|
|
|
|
|
|
ДлядостижчетвпоеточнрнияядкатоготребуетсяиспользоватьтиметодРунге |
1 |
|
|
|
|
|
|
|
|
-Куттыс |
|
|
четырьмястадиями: |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!!! = ! + 6 ! + 2 ! + 2 ! + ! , |
|
|
|
||||||||
|
|
! = !, ! , |
! |
|
|
|
|
|||||
|
|
! = ! + |
|
, ! |
+ |
, |
|
|
|
|||
|
|
2 |
2 |
|
|
|
||||||
|
|
! = ! + |
|
, ! |
+ |
! |
, |
|
|
|
||
|
|
2 |
2 |
|
|
|
||||||
МетодстакимнабоэффициромполучилназваметодРунгетовие |
! = ! + , ! + ! . |
-Кутты4 |
-гопорядка. |
|
||||||||
Дляегоп грешностисправоц нкадлива |
= ( |
! |
) |
,т.е.при |
|
уменьшениишагасеткив10раз,п |
|
|
о- |
|||
грешностьуменьшаетсяв10000раз. |
|
|
|
|
|
|
|
|
|
|||
Данныйметодможноприменять,какдляодногоуравнения,такдлясистемыуравнений, |
|
|
|
|
|
|
|
|
|
|
с- |
|
пользуяперввеходктфорпоправмнопуюиволвторомсаразделеннымэтойработы. |
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2.Нап исать файл-функцию реализметодРунгеющую |
|
-Кутты4 |
-гопорядка . Преду- |
|||||||||
смотретьвозможноиспользованияметодадляистемытьуравнений. |
|
|
|
|
|
|
|
|
|
|
|
|
|
function [yy,xx]=runge(f,x0,y0,xe,h) |
|
|
|
|
|
|
|
|
|
|
|
|
xx = x0:h:xe; |
|
|
|
|
|
|
|
|
|
|
|
|
% yy создадимввидематрицы, |
i-ястркотскаоответсвуетрой |
i-йфункции |
|
||||||||
yy = zeros(length(y0),length(xx)); yy(:,1) = y0;
for i=1:length(xx)-1
k1 = h * f(xx(i), yy(:,i));
k2 = h * f(xx(i)+h/2, yy(:,i)+k1/2);
k3 = h * f(xx(i)+h/2, yy(:,i)+k2/2);
k4 = h * f(xx(i)+h, yy(:,i)+k3); |
|
|
||
yy(:,i+1) = yy(:,i) + (k1+2*k2+2*k3+k4)/6; |
|
|
||
end |
|
|
|
|
end |
|
|
|
|
Упражнение 3. |
|
|
|
|
Выползаданупражнений1тьэтой2яработы |
|
, используяметодРунге |
-Кутты4 |
-гопоря д- |
кавместометодаЭйлера.Сравнить |
погрешности, |
полученныеприиспользова |
нииразныхметодов. |
|
4. Решение задачиКоши |
спомощьювстроенныхфункций |
MATLAB. |
|
|||
В MATLAB длярешения |
задачиКошидляс дифференциальныхстемыуравнений |
|
реализован |
|||
наборметодов: |
ode23, ode45, ode113, ode15s, ode23s, ode23t, ode23tb. |
|
|
|||
Метод ode23 реализуетметодРунге |
-Кутты2 |
-гопорядка, |
ode45 – методРунге |
-Кутты4 |
-гоп о- |
|
рядка,остальныеметоды |
– используютдругиеалгн рписанныевышетмы,которыеадаптиров |
|
|
а- |
||
ныподзадсрачизрывнымифункциядругимиособенностями.Руководство |
ode45,а другиеметодыприменятьеслиэтафункция |
MATLAB рекомен- |
||||
дуетвпервуюочередьиспользоватьфункцию |
|
|
||||
несправляетсязадачей |
. |
|
|
|
|
|
Подробописаниефуихпараметровоекций |
doc ode45. |
сприспользованиямерамиможнопосмо |
|
т- |
||
ретьвсправкеMATLAB,набрав |
|
|
|
|
|
|
Упражнение 4. |
|
|
|
|
|
|
НайтирешениезадачКошидляуравнений1 |
|
-гои2 -гопорядкав(соответствииВашимном |
|
е- |
||
ромварианта),используявстроеннуюфункци |
ode45. |
|
|
|
||
Задлявыполненияаниялабораторнойработы.
Номервариантасоответствукомпьютерапоследнцифреномера.й
№ |
1-йпорядок |
2-йпорядок |
|
вар-та |
|||
! = !!!, |
!! − 4 ! + 3 = !!, |
||
0 |
|||
|
0 = 0 |
0 = 3, ! 0 = 9 |
|
1 |
! = + , |
!! − 8 ! + 16 = !!, |
|
|
0 = 1 |
0 = 0, ! 0 = 1 |
|
2 |
! = − , |
!! + 4 = sin 2 + 1, |
|
|
0 = 1 |
0 = 1/4, ! 0 = 0 |
|
3 |
! = !, |
2 !! − ! = 1, |
|
|
0 = 0 |
0 = 0, ! 0 = 1 |
|
4 |
! = − 2 , |
!! + 5 ! + 6 = 0, |
|
|
0 = 0 |
0 = 1, ! 0 = −6 |
|
5 |
! = / , |
!! − 10 ! + 25 = 0, |
|
|
0 = 1 |
0 = 0, ! 0 = 1 |
|
6 |
! = !!, |
!! + 3 ! = 0, |
|
|
0 = 0 |
0 = 1, ! 0 = 2 |
|
7 |
! = !!, |
9 !! + = 0, |
|
|
0 = 0 |
0 = 1, ! 0 = 1 |
|
8 |
! = !, |
!! + = cos 3 , |
|
|
0 = 0 |
0 = 0, ! 0 = 0 |
9 |
! = sin , |
!! + = , |
|
0 = /2 |
0 = 1, ! 0 = 0 |