
ДИСЦИПЛИНА МММФП (4 семестр)
Лекции - каждая неделя, ПЗ 1 неделя, ЛЗ 2 неделя,
РЗ: 9 задач , ЛР -5, контрольная работа, экзамен.
Литература.
1. Амосов А.А, Дубинский Ю.А., Копченова Н.В. Вычислительные методы. М: Издательский дом МЭИ, 2008.
2. Казенкин К.О. Указания к решению задач по вычислительной математике. Приближение функций. Численное интегрирование. Численное дифференцирование. М: Издательство МЭИ. 2011.
3.Казенкин К.О. Указания к решению задач по вычислительной математике. Численное решение задачи Коши. Численное решение двухточечной краевой задачи. М: Издательство МЭИ. 2014.
6.Казенкин К.О. Амосова О.А. Численное решение задач математической физики. Стационарные уравнения. М: Издательство МЭИ. 2017.
7.Казенкин К.О. Амосова О.А. Численное решение задач математической физики. Нестационарные уравнения. М: Издательство МЭИ. 2016.
8. Амосова О.А., Вестфальский А.Е., Крупин Г.В. Упражнения по основам численных методов. М: Издательство МЭИ, 2016.
ЛЕКЦИЯ 1 . ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ (1)
§ 1.1 Введение.
В прикладных задачах часто возникает необходимость вычисления определенного интеграла
 .
.
В большинстве случаев получить значение интеграла по формуле Ньютона - Лейбница не удается. Обычно вычисление интеграла производится по формулам численного интегрирования, которые называются квадратурными формулами.
Пример.
Требуется вычислить интегральный синус
 .Эта
функция часто используется в приложениях.
.Эта
функция часто используется в приложениях.
Рассмотрим способы вычисления интеграла в фиксированной точке x=1.
ПЕРВЫЙ
СПОСОБ.
Разложим подинтегральную функцию
 в
ряд Тейлора в окрестности точки
в
ряд Тейлора в окрестности точки
 .
.



Ряд
сходится быстро. Вычисление значения
функции
 c
помощью 4-х слагаемых дает приближенное
значение 0.9460827664 . Таким образом,
получили 6 верных цифр.
c
помощью 4-х слагаемых дает приближенное
значение 0.9460827664 . Таким образом,
получили 6 верных цифр.
ВТОРОЙ СПОСОБ РАССМОТРИМ НИЖЕ.
Геометрический смысл определенного интеграла – площадь криволинейной трапеции, ограниченной осью OX, кривой f(x), и прямыми x=a и x=b (Рис.6.1.).
Численные методы интегрирования основаны на различных способах оценки этой площади, поэтому полученные формулы численного интегрирования называются квадратурными (формулами вычисления площади).


Рис. 1.1. Геометрический смысл определённого интеграла
Полная
площадь криволинейной трапеции состоит
из n
элементарных криволинейных трапеций
– элементарных площадей

Квадратурные формулы отличаются друг от друга способом оценки значения Si – площади элементарной криволинейной трапеции.
Рассмотрим получение простейших формул для часто используемой равномерной сетки.
§1.2. Постановка задачи и простейшие формулы.
Постановка
задачи.
Дан определенный интеграл:
.
Требуется найти приближенное значение
интеграла
 такое,
что
такое,
что
 .
.
Ниже будет рассмотрен подход, основанный на интерполяции подинтегральной функции полиномом, интеграл от которого легко вычисляется.
Известно,
что определенный интеграл обладает
свойством линейности. Ясно, что приближать
функцию на всем отрезке [a,b]
методом глобальной интерполяции
неэффективно. Отрезок [a,
b]
делят на n
необязательно равных частей – элементарных
отрезков.
Принято такое деление отрезка называть
сеткой, а точки x0,
x1,…,
xn
– узлами сетки. Если сетка равномерная,
то
 – шаг сетки, при интегрировании – шаг
интегрирования, а координата i-го
узла вычисляется по формуле:
– шаг сетки, при интегрировании – шаг
интегрирования, а координата i-го
узла вычисляется по формуле:
 ,
,
 (1.1)
(1.1)
Тогда исходный интеграл будет представлять собой сумму элементарных интегралов:
 (1.2)
(1.2)
Так как при интерполировании функции многочленом используются значения функции в узлах, то окончательно, формула примет вид:
 (1.3)
(1.3)
Далее
точки
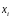 будем
называть узлами
квадратурной формулы (1.3),
будем
называть узлами
квадратурной формулы (1.3),
 - весами квадратурной формулы,
- весами квадратурной формулы,
 - остаточным членом квадратурной формулы.
При оценке эффективности формулы будем
исходить из того, что трудоемкой операцией
является вычисление функции в точке.
- остаточным членом квадратурной формулы.
При оценке эффективности формулы будем
исходить из того, что трудоемкой операцией
является вычисление функции в точке.
ФОРМУЛЫ ПРЯМОУГОЛЬНИКОВ
Элементарные
формулы прямоугольников получаются
при замене функции
 на элементарном отрезке:
на элементарном отрезке:



Составные формулы прямоугольников:
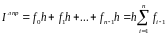


ВТОРОЙ СПОСОБ нахождения интегрального синуса.
Протабулируем
функцию
 на отрезке [0,1] c
шагом 1/4.
на отрезке [0,1] c
шагом 1/4.
t |
0 |
1/4 |
1/2 |
3/4 |
1 |
f(t) |
1 |
0.9896 |
0.9589 |
0.9089 |
0.8415 |
Применяем построенные формулы.
Левые прямоугольники

Правые прямоугольники

3. Центральные прямоугольники, но шаг в два раза больше!!

В первых двух случаях получили одну верную цифру, во втором – две.
ОЦЕНКИ ПОГРЕШНОСТЕЙ.
Выведем оценку погрешности, например, левых прямоугольников.

 =
=


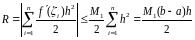
Определение.
Будем говорить, что формула имеет p-ый
порядок точности по h,
если справедлива оценка:

Таким образом, формула левых прямоугольников имеет первый порядок точности по h.
Аналогично доказывается, что формула правых прямоугольников имеет также первый порядок точности по h и аналогичную оценку погрешности.
Оценим погрешность формулы центральных прямоугольников:





Формула центральных прямоугольников имеет второй порядок точности по h.
ФОРМУЛА ТРАПЕЦИЙ
Приблизим функцию на элементарном отрезке полиномом 1-ой степени:
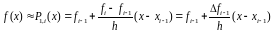
Тогда интегрируя многочлен, получим элементарную формулу трапеций:


Формула имеет простой геометрический смысл - площадь криволинейной трапеции заменяется площадью прямоугольной трапеции, равной полусумме оснований на высоту. Составная формула трапеций получается суммированием элементарных интегралов:
 (1.3)
(1.3)
Оценим величину погрешности с помощью остаточного члена интерполяции:


=
Окончательно, оценка погрешности имеет вид:
 .
(1.4)
.
(1.4)
Формула трапеций имеет второй порядок точности по h.
ФОРМУЛА СИМПСОНА.
Элементарная формула Симпсона получается с использованием интерполяционного многочлена второй степени.

Интегрируя представленный многочлен, получим элементарную формулу Симпсона:

Геометрически формула получена при замене исходной функции на элементарном отрезке параболой. (Чертеж в учебнике).
Составная формула Симпсона:
 (1.5)
(1.5)
Справедлива следующая теорема.
Теорема.
Пусть функция f(x)
имеет ограниченную четвертую производную
 на
отрезке
на
отрезке
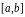 .
Тогда для формулы Симпсона справедлива
априорная оценка:
.
Тогда для формулы Симпсона справедлива
априорная оценка:
 (1.6)
(1.6)
