Частина 2

“Курс вищої математики. Частина 2.”

Крім того:

∂ϕ

∂ϕ dy

+

= 0

(2)

∂x

∂y dx

Помножимо рівність (2) на число λ і складемо з рівністю

(1).

∂f

+ ∂f

dy

∂ϕ +

∂ϕ

dy

+ λ

= 0

∂x

∂y dx

∂x

∂y dx

∂f

∂ϕ

∂f

∂ϕ dy

+ λ

+

+ λ

= 0

∂x

∂x

∂y

∂y dx

Для виконання цієї умови в усіх точках λтак, щоб виконувалася система трьох рівнянь:

∂∂fx + λ ∂∂ϕx =

∂f + λ ∂ϕ =∂y ∂y

ϕ(x, y) = 0

знайдемо невизначений коефіцієнт

0

0

Отримана система рівнянь є необхідними умовами умовного екстремуму. Проте ця умова не є достатньою. Тому при знаходженні критичних крапок потрібне їх додаткове дослідження на екстремум.

Вираз u = f(x, у)+ λϕ(x, у) називається функцією Лагранжа.

Приклад. Знайти екстремум функції f(x, у)= xy, якщо рівняння зв'язку: 2x + 3y – 5 = 0

u = xy + λ(2x +3y −5)

∂u	= y + 2λ;						∂u		= x + 3λ;
∂x							∂y
				y + 2λ = 0
				x + 3λ = 0
				2x + 3y −5 = 0
λ = −			5		;	x =	5	;	y =	5	;
		12								6
						4

Таким чином, функція має екстремум в крапці 5 ; 5 .

4 6

Використання функції Лагранжа для знаходження точок екстремуму функції називається також методом множників Лагранжа.

Вище ми розглянули функцію два змінних, проте, всі міркування щодо умовного екстремуму можуть бути поширені на функції більшого числа змінних.

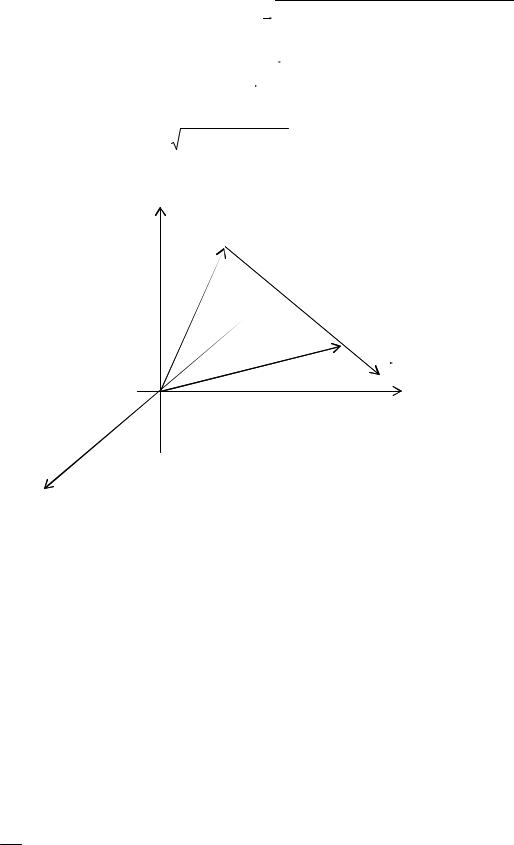
Похідна по напряму.

Розглянемо функцію u(x, у, z) в точці М( x, у, z) і точці М1( x + ∆x, у + ∆у, z + ∆z).

91

“Курс вищої математики. Частина 2.”

Проведемо через крапки М і М1 вектор S . Кути нахилу цього вектора до напряму координатних осей х, у, z позначимо відповідно γ. Косинуси цих кутів

називаються направляючими косинусами вектора S .

Відстань між крапками М і М1 на векторі S позначимо S.

∆S = ∆x2 + ∆y 2 + ∆z 2

Висловлені вище припущення, проілюструємо на малюнку: z

M

∆S

M1

S

у

x

Далі припустимо, що функція u(x, у, z) безперервна і має безперервні приватні похідні по змінним х, у і z. Тоді правомірно записати наступний вираз:

∆u = ∂∂ux ∆x + ∂∂uy ∆y + ∂∂uz ∆z + ε1∆x + ε2 ∆y + ε3∆z ,

де величини ε1, ε2, ε3 – нескінчено малі при ∆S → 0 .

З геометричних міркувань очевидно:

	∆x	= cos α;	∆y	= cosβ;	∆z	= cos γ;
	∆S		∆S		∆S

Таким чином, приведена вище рівність може бути представлені таким чином:

∆∆Su = ∂∂ux cos α + ∂∂uy cosβ + ∂∂uz cos γ + ε1 cos α + ε2 cosβ+ ε2 cos γ ;

	∂u	= lim	∆u	=	∂u cos α +	∂u cosβ +	∂u cos γ
	∂s		∆S
		∆S →0			∂x	∂y	∂z

92

“Курс вищої математики. Частина 2.”

Відмітимо, що величина s є скалярною. Вона лише визначає напрям вектора S . З цього рівняння виходить наступне визначення:

Визначення: Межа lim	∆u	називається похідній функції u(x, у, z) по
∆S →0	∆S

напряму вектора S в крапці з координатами ( x, у, z).

Пояснимо значення викладених вище за рівність на прикладі.

Приклад. Обчислити похідну функції z = x2 + y2x в крапці А(1, 2) по напряму вектора АВ. У (3, 0).

Рішення. Перш за все необхідно визначити координати вектора АВ.

АВ =(3-1; 0-2) = (2; -2) = 2 i − 2 j .

Далі визначуваний модуль цього вектора:

AB

=

8 = 2 2

Знаходимо приватні похідні функції z в загальному вигляді:

∂z

= 2x + y 2 ;

∂z

= 2yx;

∂x

∂y

Значення цих величин в крапці А :

Для знаходження направляючих косинусів вектора

АВ проводимо наступні

перетворення:

AB

r

2

r

2

r

S =

= i cos α + j cosβ =

i

−

2

j

AB

2

2

2

За величину S

береться

довільний

вектор, направлений уздовж заданого

вектора, тобто визначального напрям диференціювання.

Звідси набуваємо значень направляючих косинусів вектора АВ :

cosα =

2

;

cosβ = -

2

Остаточно отримуємо:

∂z

= 6

2

− 4

2

=

2 - значення похідної заданої функції по

∂s

2

2

напряму вектора АВ.

Градієнт.

93

“Курс вищої математики. Частина 2.”

Визначення: Якщо в деякій області D задана функція u = u(x, у, z) і деякий вектор, проекції якого на координатні осі рівні значенням функції u у відповідній крапці

∂u	;	∂u	;		∂u	,
∂x		∂y			∂z
то цей вектор називається градієнтом функції u.
gradu =	∂u r			∂u r		+	∂u	r
	∂x	i +		dy	j		∂z	k

При цьому говорять, що в області D задано поле градієнтів.

Зв'язок градієнта з похідній по напряму.

Теорема: Хай задана функція u = u(x, у, z) і поле градієнтів gradu = ∂∂ux ir + ∂dyu rj + ∂∂uz kr .

Тоді похідна ∂∂us по напряму деякого вектора S дорівнює проекції вектора gradu на вектор S .

Доказ: Розглянемо одиничний вектор							S = ircos α + rj cosβ + krcos γ і деяку
функцію u = u(x, у, z) і знайдемо скалярний твір векторів S і gradu.
		r	=	∂u	cos α +	∂u	cosβ +	∂u	cos γ
	gradu S			∂x		∂y		∂z
Вираз, що стоїть в правій частині цієї рівності є похідній функції u по напряму s.
r	∂u	. Якщо кут між векторами gradu і S позначити через, то
Тобто gradu S =	∂s

скалярний твір можна записати у вигляді твору модулів цих векторів на косинус кута

між ними. З урахуванням того, що вектор S одиничний, тобто його модуль рівний одиниці, можна записати:

gradu cos ϕ = ∂∂us

Вираз, що стоїть в правій частині цієї рівності і є проекцією вектора gradu на вектор S .

Теорема доведена.

Для ілюстрації геометричного і фізичного сенсу градієнта скажемо, що градієнт

– вектор, що показує напрям наискорейшего зміни деякого скалярного поля u в какойабо крапці. У фізиці існують такі поняття як градієнт температури, градієнт тиску і тому подібне Тобто напрям градієнта є напрям найбільш швидкого зростання функції.

З погляду геометричного уявлення градієнт перпендикулярний поверхні рівня функції.

94

“Курс вищої математики. Частина 2.”

Кратні інтеграли.

Як відомо, інтеграція є процесом підсумовування. Проте підсумовування може проводиться неодноразово, що приводить нас до поняття кратних інтегралів. Розгляд цього питання почнемо з розгляду подвійних інтегралів.

Подвійні інтеграли.

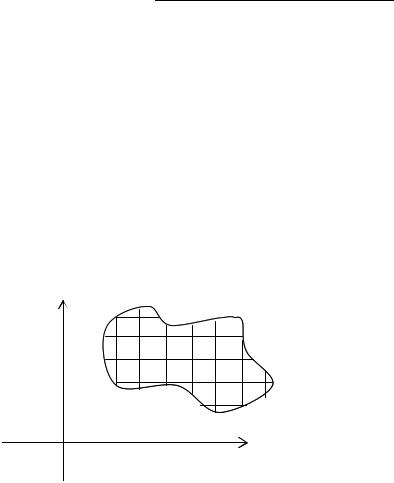
Розглянемо на площині деяку замкнуту криву, рівняння якої f(x, у)= 0.

у

0 x

Сукупність всіх крапок, лежачих усередині кривою і на найкривішій назвемо замкнутою областю ∆. Якщо вибрати точки області без урахування крапок, лежачих на кривій, область буде називається незамкнутою область ∆.

З геометричної крапки зір ∆ - площа фігури, обмеженої контуром.

Розіб'ємо область ∆ на n часткових областей сіткою прямих, віддалених один від одного по осі х на відстань хi, а по осі у – на уi. Взагалі кажучи, такий порядок розбиття наобязателен, можливе розбиття області на часткові ділянки довільної форми і розміру.

Отримуємо, що площа S ділиться на елементарні прямокутники, площі яких рівні Si = ∆xi ∆yi .

У кожній частковій області візьмемо довільну точку Р(хi, yi) і складемо інтегральну суму

i=n

∑ f (xi , yi ) Si ;

i=1

де f – функція безперервна і однозначна для всіх точок області ∆.

Якщо нескінченно збільшувати кількість часткових областей i, тоді, очевидно, площа кожної часткової ділянки Si прагне до нуля.

Визначення: Якщо при прагненні до нуля кроку розбиття області ∆ інтегральні

i=n

суми ∑ f (xi , yi ) Si мають кінцеву межу, то ця межа називається подвійним

i=1

інтегралом від функції f(x, у) по області ∆.

95

			“Курс вищої математики. Частина 2.”
	i=n
limn→∞	∑ f (xi , yi )Si	= ∫∫ f (x, y)dxdy
	i=1	∆

З урахуванням того, що Si = ∆xi ∆yi отримуємо:

i=n	i=n i=n
∑ f (xi , yi )Si = ∑∑ f (xi , yi )∆yi ∆xi
i=1	i=1 i=1

У приведеному вище записі є два знаки, оскільки підсумовування проводиться по двох змінним х і у.

Оскільки ділення області інтеграції довільне, також довільний і вибір точок Рi, то, вважаючи всі площі Si однаковими, отримуємо формулу:

∫∫ f (x, y)dydx =	∆limx→0	∑∑ f (x, y)∆y∆x
∆	∆y→0	∆

Умови існування подвійного інтеграла.

Сформулюємо достатні умови існування подвійного інтеграла.

Теорема. Якщо функція f(x, у) безперервна в замкнутій області, то подвійний

інтеграл ∫∫ f (x, y)d∆ існує.

∆

Теорема. Якщо функція f(x, у) обмежена в замкнутій області ∆ і безперервна в ній усюди, окрім кінцевого числа кусочно – гладких ліній, то подвійний інтеграл

∫∫ f (x, y)d∆ існує.

∆

Властивості подвійного інтеграла.

1) ∫∫[f1 (x, y) + f2 (x, y) − f3 (x, y)]dydx = ∫∫ f1 (x, y)dydx + ∫∫ f2 (x, y)dydx − ∫∫ f3 (x, y)dydx

∆ ∆ ∆ ∆

2)∫∫kf (x, y)dydx = k ∫∫ f (x, y)dydx

∆∆

3)Якщо ∆ = ∆1 + ∆2, то

∫∫f (x, y)dydx = ∫∫ f (x, y)dydx + ∫∫ f (x, y)dydx

∆

∆1

∆2

4) Теорема про середній. Подвійний інтеграл від функції f(x, у) рівний твору значення цієї функції в деякій точці області інтеграції на площу області інтеграції.

∫∫ f (x, y)dydx = f (x0 , y0 ) S

∆

96

“Курс вищої математики. Частина 2.”

5) Якщо f(x, у) ≥ 0 в області, то ∫∫ f (x, y)dydx ≥ 0 .

∆

6) Якщо f1(x, у) ≤ f2(x, у), то ∫∫ f1 (x, y)dydx ≤ ∫∫ f2 (x, y)dydx .

∆∆

7)∫∫ f (x, y)dydx ≤ ∫∫ f (x, y) dydx .

∆∆

Обчислення подвійного інтеграла.

Теорема. Якщо функція f(x, у) безперервна в замкнутій області, обмеженій

лініями х = а, x = b, (а < b), у = (x), ϕу = (x), ψде ϕ і ψ - безперервні функції і ϕ ≤ ψтоді

	b	ψ( x)		b	ψ( x)
∫∫ f (x, y)dxdy = ∫		∫ f (x, y)dy	dx = ∫dx		∫ f (x, y)dy
∆	a	ϕ( x)		a	ϕ( x)

уу = (x)

∆

у= (x)ϕ

аb x

Приклад. Обчислити інтеграл, якщо область ∆ обмежена лініями: у = 0, у = x2, x = 2.

у

4

						∆
0	2		x
	2	x2	2		2	y=x		2	2				4			4			5	2
∫∫ f (x, y)dxdy = ∫dx ∫			(x − y)dy = ∫(xy −	y					= ∫(x	3		x		x				x
						)					−			)dx =			−						=
				2								2			4			10
∆	0	0	0			y=0			0											0
= 4 −3,2 = 0,8

Теорема. Якщо функція f(x, у) безперервна в замкнутій області, обмеженій лініями у = з, у = d (з < d), x = (y), Φx = (y) ((y) ≤ (y)), ΨΦΨто

	d	Ψ( y)
∫∫ f (x, y)dxdy = ∫dy		∫ f (x, y)dx
∆	c	Φ( y)

Приклад. Обчислити інтеграл, якщо область ∆ обмежена лініями у = x, x = 0, у = 1, у = 2.

97

																			“Курс вищої математики. Частина 2.”
		у
		у = x							2
											∆
									1
		0							x
	2		2	2	x	2		2	2	x3				2			y	2 4				3		4			4		2	64		4
∫∫(x		+ y		)dxdy = ∫dy∫(x			+ y		)dx = ∫				+ y		x			dy = ∫			y		dy =			y			=		−		= 5
											3							1 3						12						12 12
									1								0
∆				1	0																							1

Приклад. Обчислити інтеграл, якщо область інтеграції ∆ обмежена лініями х = 0, х = у2, у = 2.

				2	y2											2							y2
∫∫(3x2 − 2xy + y)dxdy = ∫dy ∫(3x2							− 2xy + y)dx = ∫										(x3 − yx2 + yx)							dy =
																					0
∆				0	0											0
2								y	7		y	6		y	4		2				244
= ∫( y	6		5		3
		− y		+ y		)dy =				−			+							=
								7			6			4							21
0																			0

Приклад. Обчислити подвійний інтеграл, якщо область інтеграції обмежена лініями ху=1, у = x , х = 2.

	2
	1.75
	1.5
	1.25
	1
	0.75
	0.5
	0.25
		0.5	1		1.5	2		2.5
	2	x	2	y 2	x	2	x ln x			ln x
∫∫y ln xdxdy = ∫dx ∫y ln xdy = ∫				2	ln x	dx = ∫		2	−	2x	2 dx
∆	1	1/ x	1		1/ x	1

u = ln x;

dv = xdx;

x2

x

x2

1.

x ln xdx =

2

=

ln x −

dx =

ln x −

∫

1

x

2

∫2

2

du =

dx;

v =

x

2

2

2

x

2

2

1

3

x

ln x −

= 2 ln 2 −1 +

= 2 ln 2

−

.

∫x ln xdx =

2

4

4

4

1

1

ln x

t

txdt

tdt

u = t;

ln x = t;

x = e

;

−t

2.

dx =

=

=

=

e

tdt

=

∫ x2

1

∫

x2

∫

x

∫

dt

=

dx;

dv = e

x

x2 ; 4

du = dt;		= −te−t +
−t dt; v = −e−t ;

98

“Курс вищої математики. Частина 2.”

+ ∫e−t dt = −te−t − e−t = −														ln x			−	1			;
																			x
														x
2	ln x				ln x				1			2				ln 2						1							ln 2				1
∫			dx =	−			−						= −								−			+1 = −								+		;
	x	2			x					x							2					2								2			2
											1
1
	∫∫y ln xdxdy =						1								3				ln 2						1		=	1 5ln 2						−	5		=	5ln 2	−	5
3.								2 ln 2 −									+						−
															4						2							2				2			4			4		8
	∆						2																		2

Заміна змінних в подвійному інтегралі.

Расмотрім подвійний інтеграл вигляду, де змінна х змінюється

змінна у – від 1(x) до ϕ2(х).

Покладемо х = f(u, v); у = ϕ(u, v)ϕ

.

в межах від а до b, а

Тоді dx =

∂f du +

∂f

dv ;

dy =

∂ϕ du +

∂ϕ dv ;

∂u

∂v

∂u

∂v

ϕ2 ( x)

b

∫∫F(x, y)dydx = ∫dx

∫F(x, y)dy

∆

a ϕ1 ( x)

оскільки при першій інтеграції змінна х береться за постійну, то dx = 0.

∂f

du + ∂f dv = 0 тобто

∂u

∂v

пожставляя це вираз в записане вище співвідношення для dy, отримуємо:

∂ϕ

∂f ∂v

dv + ∂ϕ dv =

∂ϕ

∂f −

∂ϕ

∂f

dy = −

∂v

∂u

∂u

∂v

dv

∂f

∂u

∂f ∂u

∂v

∂u

∂ϕ

∂f

∂ϕ

∂f

∂f

∂f

Вираз

−

=

∂u

∂v

=

i

називається визначником Якобі або Якобіаном

∂v

∂u

∂u

∂v

∂ϕ ∂ϕ

∂u

∂v

функцій f(u, v) і ϕ(u, v).

(Якобі Карл Густав Якоб – (1804-1851) німецький математик)

Тоді

Оскільки при першій інтеграції приведений вище вираз для dx приймає вигляд dx = ∂∂uf du ( при першій інтеграції вважаємо v = const, dv = 0), то при зміні порядку інтеграції, отримуємо співвідношення:

	V2	Θ2 (v)
∫∫F(x, y)dydx = ∫dv		∫F( f (u,v),ϕ(u, v))		i		du
∆	V1	Θ1 (v)

Подвійний інтеграл в полярних координатах.

Скористаємося формулою заміни змінних:

∫∫F (x, y)dxdy = ∫∫F ( f (u, v),ϕ(u, v)) i dudv

∆∆

При цьому відомо, що

99

“Курс вищої математики. Частина 2.”

В цьому випадку Якобіан має вигляд:

∂x

∂x

cos θ

−ρsin θ

i

=

∂ρ

∂θ

=

= ρcos

2

θ+ ρsin θ = ρ

∂y

∂y

sin θ

ρcos θ

∂ρ

∂θ

Тоді Тут τ - нова область значень

Потрійний інтеграл.

При розгляді потрійного инеграла детально не зупинятимемося на всіх тих теоретичних викладеннях, які були детально розібрані стосовно подвійного інтеграла, оскільки істотних відмінностей між ними немає.

Єдина відмінність полягає в тому, що при знаходженні потрійного інтеграла інтеграція ведеться не по двох, а по трьом змінним, а областю інтеграції є не частина площини, а деяка область в техмерном просторі.

∫∫∫ f (x, y, z)dxdydz =	∆limx→0 ∑∑∑ f (x, y, z)∆x∆y∆z
r	∆y→0	v
	∆z→0
Підсумовування проводиться по області v, яка обмежена деякою поверхнею ϕ(x,
у, z) = 0.	x2	y2 z2
∫∫∫ f (x, y, z)dxdydz = ∫∫∫ f (x, y, z)dzdydx
r	x1	y1 z1

Тут х1 і х2 – постійні величини, у1 і у2 – можуть бути деякими функціями від х або постійних величин, z1 і z2 – можуть бути функціями від х і у або постійними величинами.

					Приклад.			Обчислити інтеграл
1 x2 xy				2				1 x2	2	z 2					xy					1 1 x2				2	2 2	1 1 x2		4 3	1 1		4		y 4			x2
∫∫∫x					yzdzdydx = ∫∫x																	∫∫x			yx y dydx =		∫∫x	y dydx =		∫x
										y					dydx =																					dx =
0 0 0								0 0			2				0					2 0 0						2	0 0		2	0			4			0
	1	1	x		4 x8		1	1				1		1					1 =		1
=		∫				dx =		∫x12 dx =									x13						.
2		0			4	8		0			8			13					0	104

Заміна змінних в потрійному інтегралі.

Операція заміни змінних в потрійному інтегралі аналогічна соответсвующей операції для подвійного інтеграла.

Можна записати:

∫∫∫F(x, y, z)dxdydz = ∫∫∫F( f (u,v,

r

τ

∂x

∂u i = ∂∂uy

∂z

∂u

w),ϕ(u, v, w),ψ(u, v, w)) i dudvdw

∂x ∂x

∂v ∂w ∂y ∂y

∂v ∂w ∂z ∂z

∂v ∂w

100