ОнВ экз. Высшая математика 1 курс 2 сем

Интегралы:

1. Понятие первообразной функции и неопределённого интеграла:

Первообразная f(x) - такая функция, при которой F(x)'=f(x). Неопределённый интеграл-это совокупность всех первообразных функции f(x). Обозначается знаком ( и dx.

2 . Таблица основных интегралов. «Неберущиеся» интегралы.

3. Свойства неопределённого интеграла. Непосредственное интегрирование.

1)дифференцирование и интегрирование – это два взаимно обратных действия

2)неопределённый интеграл от дифференциала функции равный этой функции

3)постоянный множитель можно вынести за знак интеграла

4)сумма в интеграле равна сумме интегралов

Непосредственное интегрирование - преобразование интеграла в табличные.

4. Замена переменной.

Метод замены переменной реализуется двумя способами:

– Подведение функции под знак дифференциала;

– Собственно замена переменной. (t=3x+1 x=(t-1)/3 dx=dt/3)

5. Интегрирование по частям.

6. Интегрирование рациональных дробей.

Если интеграл не табличный, раскладываем, всё что можем разложить, потом либо метод неопределённых коэффициентов, либо деление в столбик.

7 . Интегрирование рациональных дробей I , II , III типа. 8. Интегрирование рациональных дробей IV типа.

9 . Разложение рациональной дроби на простейшие дроби. Метод неопределённых коэффициентов.

10. Интегрирование тригонометрических функций.

И спользуется ряд методов: использование тригонометрических формул (н.п.: sin(a)*cos(b)=дробь); понижение степени подынтегральной функции(cos(x)^2); метод замены переменной (заменяем "неудобную" f(x) на t) и универсальная тригонометрическая подстановка.

11. Интегрирование некоторых иррациональных функций: x в корнях разных степеней (замена на t в общей степени), иррациональные дроби (формулы умножения).

1 2. Интегрирование некоторых иррациональных функций:

ДИфФУРЫ

13. Определение дифференциального уравнения, его порядка и решения.

Диф.ур. - уравнение, связывающее функции и их производные. Порядок определяется высшим порядком производной. Решение - функция y=f(x), при подстановке которой в диф.ур. получается тождество.

14.Дифференциальные уравнения 1-го порядка. Задача Коши. Геометрическая интерпретация теоремы Коши.

Диф.ур. 1 пор. - ур., в котором есть y' и нет производных высших порядков (y'', y'''). Задача Коши - нахождение решения диф.ур., удовлетворяющее "начальным условиям" y(x₀)=y₀. Геом. инт. з. Коши - найти интегральную кривую диф.ур., проходящую через заданную точку M(x₀,y₀).

15. Уравнения с разделяющимися переменными.

Д ля решения таких уравнений переносим игреки+dy влево, иксы+dx вправо и интегрируем.

16. Однородные дифференциальные уравнения первого порядка.

Одн. д.у. 1 пор. называют уравнения, не имеющие дифференциалы высших порядков (y'', y''') и правая часть которых = 0.

Имеет вид y'+p(x)*y=q(x), где q(x) равно 0.

Для проверки однородности: заменяем все х и у на λх и λу (производные не трогаем). Если получиться сократить все λ, то ур. однородное.

Сначала смотрим можно ли разделить переменные. Если нет, то данное ур. решается с помощью одной замены у=tx и y'=t'x+t.

17. Линейные дифференциальные уравнения первого порядка.

Уравнение имеет вид y'+p(x)*y=q(x), где q(x) не равно 0.

Р ешение: сначала смотрим можно ли разделить переменные. Если нет, проверяем на однородность. Неоднородное, делаем замену:

18.Уравнение Бернулли.

Оно похоже на линейное неодн. диф.ур.: y'+p(x)*y=g(x)*y^альфа. Одно из очевидных ЧАСТНЫХ решений y=0. Ур. Бернулли с помощью замены сводится к линейному неоднородному уравнению первого порядка.

19. Уравнения высших порядков.

Диф. ур. высших порядков содержат производные высших порядков: y'', y''' и т.д.

20. Дифференциальные уравнения, допускающие понижение порядка.

Имеют вид y⁽ⁿ⁾=f(x), где n - производная энного порядка. Решается с помощью диффиринцирования f(x) n раз. (y''=f(x) - 2 раза, y'''=f(x) - 3 раза). Иногда заменяем y' на z.

21. Линейные однородные дифференциальные уравнения. Простейшие свойства решений. Линейные неоднородные дифференциальные уравнения.

Имеет вид y'+p(x)*y=q(x), где q(x) в однородных диф. ур. = 0, а в неодн. не равно 0. В однородных уравнениях производим замену у=tx и y'=t'x+t, в неодн. - y=u*v.

22. Фундаментальная система решений. Определитель Вронского.

Ф унд. сист. реш. - совокупность линейно независимых частных решений диф. ур. Для того чтобы решения у1(х), у2(х), уn(х) составляли фундаментальную систему решений достаточно, чтобы определитель Вронского этой системы был отличен от нуля.

23 будет на след листе. 24. 25. 26. (Виды решений при разных D):

Решаем характерист. ур. Если при решении характ. ур. D>0, то общ. реш. y=C1*e^(k1*x)+C2*e^(k2*x); D=0: y=(C1+C2*x)e^(k1*x); D<0: y=(C1*cos(b*x)+C2*sin(b*x))e^a*x.

27. Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами.

О бщее решение находится как и в случае ур. 2 пор. Алгоритм: 1)решаем характ. ур.; 2)по характеру корней выписать частные лин. решения (их кол-во = n)

23.Теорема о структуре общего решения линейного однородного дифференциального уравнения.

П усть y1(x), y2(x),…, yn(x) фундаментальная система решений линейного однородного дифференциального уравнения. Тогда его общее решение имеет вид y(x)=С1*y1(x)+ С2*y2(x)+…+ Сn*yn(x) (2)

28.Теорема о структуре общего решения линейного неоднородного дифференциального уравнения.

О бщее решение неоднородного уравнения представляется как сумма какого-нибудь частного решения и общего решения соответствующего однородного уравнения.

29.Метод вариации произвольных постоянных.

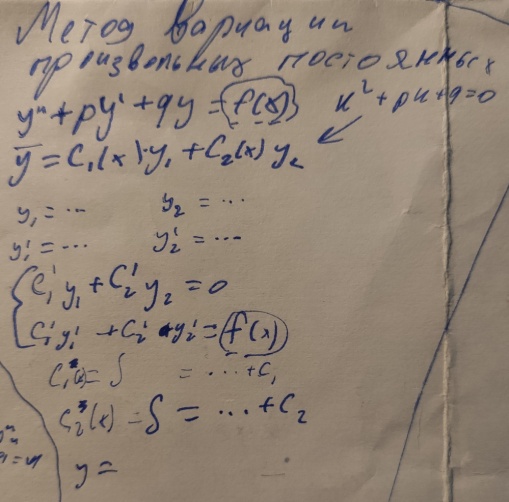
30.Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Метод неопределенных коэффициентов.

Правая часть f(x)= P_n(x)*e^(∝x).

31.Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Метод неопределенных коэффициентов.

П равая часть f(x)= P(x)e^(∝x) cosβx+Q(x) e^(∝x) sinβx.