Все за 2й курс / Лекция 11

Лекция 11 . Численное решение начально-краевой задачи

для уравнения теплопроводности.

Литература к лекции. [1] Казенкин К.O., Амосова О.А.. Численное решение задач математической физики. Нестационарные уравнения .М: Изд-во МЭИ, 2016.

§ 11.1 Материалы к выполнению ЛР 8

Будем рассматривать первую краевую задачу с постоянными коэффициентами для уравнения теплопроводности.

(11.1)

Для построения разностной схемы будем использовать метод конечных разностей.

Суть метода в том, что все разностные производные будем заменять разностными аналогами. Заменим производную по t правой разностной производной, а вторую производную по х известным равенством :

,

Отметим, что производная по t аппроксимирована с первым порядком точности по τ , а вторая производная аппроксимирована со вторым порядком точности по h. Следовательно, построенная схема будет иметь первый порядок аппроксимации по t и второй по h. При этом мы использовали следующий трехточечный шаблон:

Запишем разностное уравнение, аппроксимирующее исходное дифференциальное уравнение: , i=1…n-1, j=0…m-1

Здесь . Индексы i и j взяты таким образом, чтобы разностное уравнение

было определено во всех внутренних узлах сетки. Дополним разностные уравнения значениями на нулевом слое (начальная температура) , i=0…n и в граничных точках (граничные условия): в левой точке , j=0…m и в правой точке , j=0…m. Окончательно, получили систему равенств для нахождения приближенного решения задачи (11.1):

(11. 2)

Система (11.2 ) называется явной разностной схемой для уравнения теплопроводности.

Преобразуем разностное уравнение так: выразим неизвестное значение на слое j+1

через предыдущие значения:

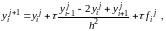
Для упрощения расчетов введем параметр и соберем слагаемые с одинаковыми индексами. Тогда формула для расчетов примет такой вид:

.

Окончательно, расчеты проходят следующим образом:

В лекции 10 в качестве тестового примера была построена задача:

,

для которой известно было точное решение: .

ПРИМЕР задачи из ЛР 8.

Задача 8. 1. Промоделировать установление процесса теплопроводности в стержне. Для этого рассмотреть две задачи: начально-краевую 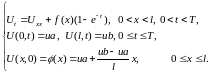(8.1)

(8.1)

и краевую (8.2).

(8.2)

Очевидно, что при .

Рассмотрим пример построения тестового примера для задач (8.1) - (8.2):

Начнем с задачи (8.2):

Пусть 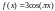, длина стержня , ,

Для нахождения решения дважды проинтегрируем уравнение:

Таким образом, получили решение уравнения

Найдем константы и :

,

,

Окончательно, получили решение краевой задачи:

Построим задачу (8.1). Возьмем начальную температуру . Тогда задача (8.1) примет вид:

Если все верно сделано, то

§ 11.2 Неявная разностная схема

Продолжим рассматривать построение разностных схем для первой краевой задачи с постоянными коэффициентами для уравнения теплопроводности.

(11.3)

Чисто неявной разностной схемой (схемой с опережением) называется разностная схема, использующая следующий шаблон:

Разностное уравнение, аппроксимирующее исходное дифференциальное уравнение на таком шаблоне имеет вид: , i=1…n-1, j=0…m-1 . Схема имеет тот же порядок аппроксимации, что и явная схема: первый порядок по и второй по h, запишем это как (o большое от + )

Решение задачи также находится по слоям, начиная с j=1. Однако для нахождения решения на каждом слое придется решать систему уравнений. Рассмотрим вопрос более подробно. Неявная разностная схема имеет вид:

(11.4)

Для нахождения решения заполним нижний слой значениями начальной температуры,

значения , . Преобразуем разностное уравнение системы так:

. Возьмем и перенесем все неизвестные значения в одну часть, а значения на предыдущем слое и известные

значения в другую.

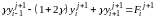, , i=1…n-1.Запишем более подробно как выглядит СЛАУ, например, на первом слое по времени.

Очевидно, что получена система уравнений с трехдиагональной матрицей системы, которая может быть решена методом прогонки. Условием применимости метода прогонки является условие диагонального преобладания. Очевидно, что оно выполнено. На остальных слоях матрица системы будет иметь такой же вид. Различие будет в правой части, она зависит от временного слоя.

Для 1-го и остальных слоев матрица системы имеет вид:

Вектор правой части имеет вид: на первом слое

, на j+1 -ом слое

Алгоритм применения неявной разностной схемы.

1. Ввод исходных данных:

2. Задаем параметры разностной схемы: , 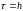(выбрано произвольно), .

3. Формирование матрицы A

4.Задание решения на начальном слое:

5. Нахождение решения на j-ом слое:

формирование вектора правой части

,

Решение системы

6. Вывод матрицы решения y на печать.

Пример применения РС для решения задачи см. [1], (§ 2.1)

§11.3. Исследование устойчивости разностных схем.

Рассмотрим вопрос об устойчивости разностных схем. Для исследования

возьмем такую задачу:

(11.3)

Отличие задачи (11.3) от (11.1) в том, что рассматривается однородное уравнение вместо неоднородного уравнения и добавлен постоянный коэффициент теплопроводности к=const >0.

Для исследования устойчивости применим метод гармоник. Суть его состоит в том, что составляется уравнение для погрешности возмущения . Затем анализируют в каком случае погрешность будет не возрастать. Так как нет правой части уравнения, то исследуется устойчивость задачи по начальным данным.

Явная разностная схема. Исходное уравнение имеет вид:

Если взять «возмущенную» задачу, то решение также должно удовлетворять

разностному уравнению: . Теперь вычитая из

последнего равенства предыдущее, в силу линейности получим уравнение для погрешности : .

Будем искать решение задачи в виде , где I- мнимая единица, p- произвольное число, q- подлежит определению. Заметим, что если , то погрешность расти не будет с увеличением j, в противном случае при 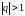будет наблюдаться рост величины погрешности при .

Подставим предполагаемый вид решения в уравнение:

Сократим уравнение на :

Найдем отсюда q:

Запишем условие устойчивости: .

Таким образом, получили, что шаг по времени должен быть порядка .

Условие (11.4)

называется условием устойчивости явной разностной схемы.

В [1] (§ 2.2) показано как происходит рост погрешности при невыполнении условия (11.4) даже в случае, когда погрешность внесена только в одну точку начального слоя.

Неявная разностная схема. Исходное уравнение:

Проделав те же рассуждения что и выше, для погрешности возмущения получим уравнение: . Подставим предполагаемый вид решения в уравнение:

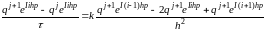
Сократим уравнение на :

Найдем отсюда q:

. В знаменателе стоит число большее или равное 1, поэтому

при любых p, h, k, . Это означает, что выбор не зависит от h.

Такие схемы называются абсолютно устойчивыми.

§ 11.4. Построение разностной схемы для уравнения с переменным коэффициентом

теплопроводности.

В случае, когда стержень состоит из нескольких материалов, уравнение теплопроводности имеет следующий вид:

(11.5)

Здесь к=k(x) – положительно определенная функция. Для того, чтобы разностная схема имела порядок аппроксимации , следует воспользоваться результатами

лекции 9 . Запишем неявную разностную схему для задачи (11.5):

Преобразуем разностное уравнение:

Здесь. , , , i=1..n-1.

Далее задача решается по алгоритму, изложенному выше для неявной схемы.

Однако в этом случае матрица системы уже не является матрицей с постоянными коэффициентами, хотя для каждого слоя она является одинаковой:

Замечание. Если решать эту задачу по явной схеме, то нужно выбрать шаг по времени из условия устойчивости. Для переменного коэффициента теплопроводности это условие имеет вид: 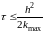, здесь . Естественно, что оно является очень ограничительным.