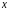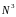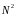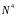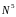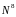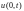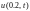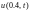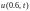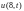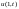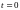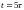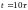Все за 2й курс / Лекция 12
.docx
Лекция 12 . Применения метода конечных разностей для решения
нестационарных задач математической физики.
Литература к лекции. [1] Казенкин К.O., Амосова О.А.. Численное решение задач математической физики. Нестационарные уравнения .М: Изд-во МЭИ, 2016.
§ 12.1 Семейство разностных схем с весами.
Продолжим рассматривать построение разностных схем для первой краевой задачи с постоянными коэффициентами для уравнения теплопроводности.
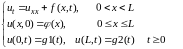 (12.1)
(12.1)
Рассмотренные
выше схемы (явная и неявная ) имели
порядок аппроксимации
 .
.
Кажется
вполне логичным, заменить производную
по t
центральной разностной производной и
тем самым получить 2-ой порядок
аппроксимации по
 :
:
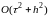 .
.
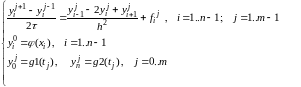 (12.2)
(12.2)
Оказывается, что эта схема непригодна, так как она является абсолютно неустойчивой.
Если исследовать схему на устойчивость методом гармоник, то получим следующее характеристическое уравнение:
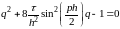
Корни этого уравнения равны:

Один из корней всегда по модулю больше 1.
Обычно поступают иначе.
Применяют семейство схем с весами.
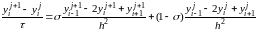 (12.3)
(12.3)
Где
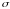 -
параметр.
-
параметр.
При
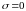 имеем явную схему,
имеем явную схему,

 имеем
чисто неявную схему,
имеем
чисто неявную схему,
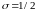 имеем
симметричную схему,
имеем
симметричную схему,
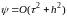
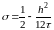 имеем
схему повышенного порядка аппроксимации
,
имеем
схему повышенного порядка аппроксимации
,
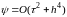 .
.
Известно,
что все схемы с
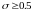 абсолютно устойчивы. Схема повышенного
порядка аппроксимации также является
абсолютно устойчивой РС. При
абсолютно устойчивы. Схема повышенного
порядка аппроксимации также является
абсолютно устойчивой РС. При
 РС
являются неявными схемами. Для нахождения
решения на каждом временном слое
требуется решать систему уравнений .
Обычно мы решаем методом прогонки.
РС
являются неявными схемами. Для нахождения
решения на каждом временном слое
требуется решать систему уравнений .
Обычно мы решаем методом прогонки.
Заметим, что при этом используется “шеститочечный шаблон”.
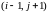
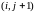
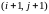
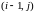
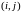
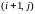
§ 12.2 Двумерная задача теплопроводности.
Рассмотрим задачу о нагревании прямоугольной пластины.
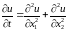 ,
,
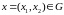 ,
,
 (12.4)
(12.4)

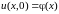 ,
,
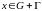
Здесь
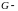 прямоугольник,
прямоугольник,
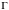 - граница прямоугольника.
- граница прямоугольника.
Введем разностные операторы:
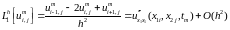
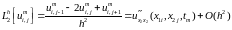
Тогда разностная схема примет вид:
 (12.5)
(12.5)
Формулы (12.5) определяют явную разностную схему. Решение во всех внутренних точках находится по формулам:

Недостатком
этой схемы является условная устойчивость:
схема устойчива при соотношении шагов:
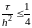 .
Пусть h=0.01.
Тогда
.
Пусть h=0.01.
Тогда
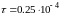 .
Чтобы получить решение в t=T=1
нужно сделать 40000 шагов по времени. Это
неприемлемое число арифметических
действий.
.
Чтобы получить решение в t=T=1
нужно сделать 40000 шагов по времени. Это
неприемлемое число арифметических
действий.
Неявная разностная схема – абсолютно устойчивая.
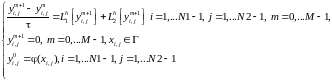 12.6)
12.6)
На
каждом временном слое нужно решать
систему уравнений, содержащую
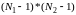 неизвестных.
неизвестных.
Начиная
с 50-х годов 20 века стали развиваться
методы, основанные на сведении многомерной
задачи к последовательности одномерных
задач. Эти методы сочетают в себе
положительные стороны явной и неявной
схемы: абсолютную устойчивость и простоту
решения. Рассмотрим так называемый
метод переменных направлений. В этом
методе переход от слоя m
к слою m+1
осуществляется в два этапа: вводится
дополнительный
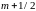 слой и уравнение разбивается на два:
слой и уравнение разбивается на два:
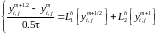 (12.7)
(12.7)
На
втором этапе , пользуясь найденными
значениями
 находим
находим
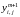 из системы уравнений:
из системы уравнений:
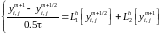 (12.8)
(12.8)
Уравнение
(12.7) является неявным по первой переменной,
а второе уравнение – по переменной
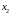 .
.
Рассмотрим подробно первое уравнение системы:
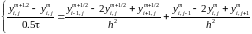
Приведем уравнение к стандартному виду:
 ,
где
,
где
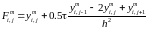
При каждом фиксированном j=1,2,..N1 методом прогонки по i решаем СЛАУ . После того как найдены значения решаем следующие уравнения:
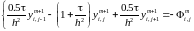
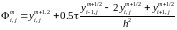
Также методом прогонки.
Приведем для сравнения число арифметических действий, требуемых для решения сеточных уравнений. Здесь N1=N2=N.
|
Явная схема |
Неявная схема |
Метод переменных направлений |
|
|
|
|
|
|
|
|
|
|
|
|
§ 12.3. Применение метода конечных разностей для уравнения колебаний струны.
Рассмотрим еще один пример – начально-краевая задача для уравнения колебаний струны.
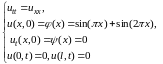 .
.
Методом разделения переменных можно найти аналитическое решение задачи.
Оно имеет вид:
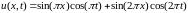 .
.
Перейдем
к построению разностной схемы: возьмем
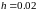 ,
,
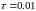 ,
обозначим
,
обозначим
 .
.

Тогда разностная схема примет следующий вид:
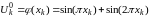 k=1,..n-1
k=1,..n-1
 k=1,..n-1
k=1,..n-1
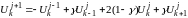 ,
k=1,..n-1
,
k=1,..n-1

Результаты вычислений на нескольких временных слоях приведены в следующей таблице
( для удобства в таблицу внесены значения не во всех точках полученного массива):
|
|
|
|
|
|
|
|
|
0 |
1.5388 |
1.5388 |
1 |
0.3633 |
-0.3633 |
0 |
|
0 |
0.4143 |
0.6716 |
0.7070 |
0.6732 |
0.4168 |
0 |
|
0 |
-0.9512 |
-0.5879 |
-0.0002 |
0.5876 |
0.9510 |
0 |
|
0 |
-0.4144 |
-0.6718 |
-0.7072 |
-0.6734 |
-0.4169 |
0 |
Сравним с аналитическим решением в тех же точках:
|
|
|
|
|
|
|
|
|
0 |
1.5388 |
1.5388 |
1 |
0.3633 |
-0.3633 |
0 |
|
0 |
0.4156 |
0.6725 |
0.7071 |
0.6725 |
0.4156 |
0 |
|
0 |
-0.9510 |
-0.5878 |
0 |
0.5878 |
0.9511 |
0 |
|
0 |
-0.4156 |
-0.7071 |
-0.7071 |
-0.6725 |
-0.4156 |
0 |
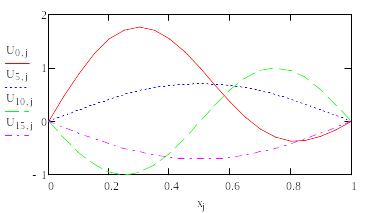
Ниже приведены профили струны в тех же точках по времени, что и в таблице. Так как решения различаются мало, то графики построены по массиву точного решения.