Содержание

Билет 13 2

Билет 14 12

Билет 15 15

Билет 16 20

Билет 13

Сначала тут пойдёт пояснение, что вообще такое за зверь эти ваши кортежи и прочее, и с чем их вообще едят. Затем же – конкретные ответы на вопросы. Пишущий этот текст Егор из прошлого наивно таит в глубине сердца надежду, что читающие это люди поймут хотя бы 30% написанного ниже…

К слову, настоятельно рекомендую прочитать пункт 2.4 (страницы 25-33) или хотя бы пункт 2.4.1 (понятие отношения, страницы 25-26) файла «Основы баз данных», который будет выслан вместе с этим файлом. Кроме того, рекомендую к просмотру лекцию хуй проссышь откуда, зато изложенную БОЛЕЕ МЕНЕЕ понятным языком: https://www.youtube.com/watch?v=npY_lb-ybW8.

P.S. Всё, что написано курсивом – попытка в пояснение этого дерьма.

P.P.S. Материал, приведённый до конкретных ответов на вопросы настолько обязателен к прочтению и хотя бы примерному понимаю, что, если вы его не прочитаете, вам до самой пересдачи буду сниться я, бегущий за вами с кипой документов по реляционной алгебре, исчислениям и прочей заумной хуете.

Итак, приступим.

В реляционных базах данных кортеж — это элемент отношения, строка таблицы; упорядоченный набор из N элементов. Для N-арного отношения кортеж представляет собой упорядоченный набор из N значений, по одному значению для каждого атрибута отношения.

Небольшой пример:

Таблица – наиболее удобная форма отображения отношения. Если столбцами таблицы являются некоторые подмножества множества X, а элементами таблицы – значения элементов множества X, то строками являются кортежи заданного отношения.

А теперь начнём издалека:

Соответствие, заданное на элементах одного множества X, называют отношением (relation).

Правила, заданные отношением, формируют множество упорядоченных последовательностей элементов множества X. В свою очередь это множество является подмножеством декартового произведения множества X.

Реляционное исчисление основано на разделе математической логики, который называется исчислением предикатов. Основным средством реляционного исчисления является понятие переменной кортежа (также называемой переменной области значений). Коротко говоря, переменная кортежа – это переменная, «изменяющаяся на» некотором заданном отношении, т.е. переменная, допустимыми значениями которой являются кортежи заданного отношения. Другими словами, если переменная кортежа V изменяется в пределах отношения r, то в любой заданный момент переменная V представляет некоторый кортеж t отношения r. Например, запрос «Получить номера поставщиков из числа тех, которые находятся в Лондоне» может быть выражен на языке QUEL так:

RANGE OF SX IS S;

RETRIEVE (SX.S#) WHERE SX.CITY = “London”;

Переменной кортежа здесь является переменная SX, которая изменяется на отношении, представляющем собой текущее значение переменной – отношения S (оператор RANGE – оператор определения этой переменной). Оператор RETRIEVE означает следующее: «Для каждого возможного значения переменной SX выбирать компонент S# этого значения тогда и только тогда, когда его компонент CITY имеет значение ‘London’».

В связи с тем, что реляционное исчисление основано на переменных кортежа, его первоначальную версию называют также исчислением кортежей.

В общем виде любое выражение исчисления кортежей записывается как

{x(R) | f(x)}, где f – некоторый предикат над переменным кортежем х.

Это выражение обозначает отношение r(R), которое состоит из тех кортежей t(R), для которых f(t) истинно.

Согласно Д. Мейеру, основными строительными блоками для формул типа f(t) являются атомы трёх типов:

1. Если r – имя отношения из домена имён d, а х – переменный кортеж, то r(x) – атом, означающий, что .

2. Если х и у – переменные кортежи (не обязательно различные), 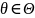– знак сравнения, А и В – атрибуты из U, которые θ-сравнимы, то х(А) θ у(в) - атом.

3. Если х – переменный кортеж, – знак сравнения, А и В – атрибуты из U, которые θ-сравнимы и с – константа из dom (A), то с θ х(В) – атом, если с – константа из dom (В), то х(А) θ с – атом.

Из атомов строятся рекурсивные формулы с помощью логических связок (НЕ), (И), (ИЛИ), (Существует) и (для каждого). Построение выражений производится по шести правилам:

1. Каждый атом – формула.

2. Если f - формула, то f – формула.

3. Если f и g– формулы, то f g и f g– формулы.

4. Если х – переменный кортеж, f – формула, включающая x, а R - подмножество U, то x(R) f – формула (она истинна, если существует кортеж t над R, при подстановке которого вместо x в f формула становится истинной).

5. Если x – переменный кортеж, f – формула, включающая x, а R –подмножество U, то x(R) f – формула (она истинна, если для каждого кортежа t над R формула f становится истинной при подстановке t вместо x).

6. Если f – формула, то и (f) – формула.

Приоритет связок в выражениях следующий: или (равный приоритет), , , . Скобки изменяют порядок действий, установленный приоритетом связок.

В реляционном исчислении с переменными-кортежами справедливо следующее утверждение: для любого выражения реляционной алгебры существует эквивалентное ему безопасное выражение в реляционном исчислении с переменными-кортежами. В исчислении кортежей на вид формул накладываются определенные ограничения, чтобы исключить выражения, не имеющие смысла. Формулы, удовлетворяющие этим ограничениям, называют разрешёнными формулами, а соответствующие выражения – безопасными.

В реляционном исчислении важными являются понятия – свободные и связанные вхождения переменной в формулу. Они несут такую же семантическую (смысловую) нагрузку, как и глобальные и локальные переменные в программе. Кванторы, т.е. связки и соответствуют декларациям (объявлениям), они связывают вхождения переменных, находящихся в сфере их действия. Кванторы также используются для описания типа переменной в формулах.

Свободные и связанные вхождения переменных определяются рекурсивно одновременно с type (x, f) - типом переменной x в формуле f и men (x, f) – множеством ссылок переменной x в f. И тип переменной type (x, f), и множество ссылок men (x, f) определены только в случае, если x имеет свободное вхождение в f (т.е. «x появляется в f свободно). Понятия свободы, связанности, типа и множества ссылок используются для определения класса разрешённых формул через ограничения на употребление различных связок.

Не совсем относится к кортежам, но удобно плюс наглядно поясняет часть вышесказанного: смотри рисунок 1.

Рисунок 1 – Свободное и связанное вхождение переменной в формулу (пример 1)

То есть, по сути (и кстати ОЧЕНЬ грубо говоря), связанное вхождение – это когда перед использованием переменной её определяют с помощью квантора, а свободное вхождение, соответственно, когда не определяют, а просто снихуя начинают использовать (нечто вроде определения глобальной переменной для свободного вхождения и локальной для связанного. Пушо глоабльная определена где-то там, за кулисами, вот её и не видать, поэтому и кажется, будто бы она начинает использоваться снихуя, она СВОБОДНА от нашего взора, а локальную переменную мы определяем непосредственно перед использованием в функции, она на виду, она СВЯЗАНА нашим взглядом. Вот такую аналогию юзайте. Работает о3о). (На деле всё не совсем так (но почти, чекайте дополнительный файл и видос), но, блять, как объяснить это иначе понятным нам языком я уже просто не ебу).

После написания полугневной тирады выше, нашёл пример ещё получше. Старый убирать не буду, пускай тоже используется в роли пояснения, а теперь: Внимание-внимание! Смотрим рисунок 2.

Рисунок 2 – Свободное и связанное вхождение переменной в формулу (пример 2)

Выражением реляционного исчисления кортежей называется конструкция вида target_list WHERE WFF. Значением выражения является отношение, тело которого определяется WFF, а множество атрибутов и их имена – целевым списком.

Вопрос 13.1. Указать подмножество разрешенных выражений (подмножество разрешенных формул) реляционного исчисления кортежей. Свободное и связанное вхождение переменной в формулу. Тип переменной в формуле. Множество ссылок переменной в формуле. Примеры разрешенных и не разрешенных выражений реляционного исчисления кортежей.

Ответ:

Разрешённые выражения (разрешённые формулы).

Атомарные формулы всегда разрешены, если удовлетворяют требованиям на домены и знаки сравнения:

1. f = r(x), r(R), тип вхождения x в f – свободный type(x,f) = R

2. f = x(A) θ y(B), тип вхождений x и y в f – свободный type(x,y), type(y,f) – не определены men(x,f) = A, men(y,f) = B

3. f = x(A) θ c, тип вхождения x в f – свободный type(x,f) – не определён men(x,f) = A

4. g – разрешённая формула, f = ¬g f – разрешена

типы вхождения переменных в f, а также типы и множества ссылок, сохраняются по сравнению с типами вхождения переменных в g type(x, f) = type(x, g), men(x, f) = men(x, g)

5. g, h – разрешенные формулы

f = g h f – разрешена

Типы вхождения переменных в f сохраняются по сравнению с типами вхождения переменных в g.

type(x, f) = type(x, g) = type(x, h), если определены type(x, g) и type(x, h)

type(x, f) = type(x, g), если определен type(x, g), но не определен type (x, h); men(x, h) type (x, g) men (x, f) = men(x, g) men(x, h), если не определены type(x, g) и type(x, h)

6. g, h – разрешенные формулы

f = g h f – разрешена

Типы вхождения переменных в f сохраняются по сравнению с типами вхождения переменных в g.

type(x, f) = type(x, g) = type(x, h), если определены type(x, g) и type(x, h)

type(x, f) = type(x, g), если определен type(x, g), но не определен type (x, h); men(x, h) type (x, g) men (x, f) = men(x, g) men(x, h), если не определены type(x, g) и type(x, h)

7. g – разрешённая формула

f = x(R)g

f разрешена, если тип вхождения x в g – свободный, type(x, g) = R (если type(x, g) определён в g) или men(x, g) R

тип вхождения x в g – связанный type(x, f) и men(x, f) не определены

типы вхождения переменных, x, в f сохраняются по сравнению с типами вхождения переменных в g.

8. g – разрешённая формула

f = x(R)g

f разрешена, если тип вхождения x в g – свободный, type(x, g) = R (если type(x, g) определён в g) или men(x, g) R

тип вхождения x в g - связанный type(x, f) и men(x, f) не определены

типы вхождения переменных, x, в f сохраняются по сравнению с типами вхождения переменных в g.

9. g – разрешённая формула

f = (g) f – разрешена

типы вхождения переменных в f, а также типы и множества ссылок, сохраняются по сравнению с типами вхождения переменных в g type(x, f) = type(x, g), men(x, f) = men(x, g)

Свободное и связанное вхождения переменной в формулу:

Квантор связывает ту переменную, которая следует за ним

Квантор имеет область действия.

Область действия внешнего квантора в формулах f или f – это подформула f. (далее примеры в виде пикч)

Вхождение переменной, не являющееся связанным, - свободное вхождение.

Переменная, имеющая свободное вхождение, - свободная переменная формулы.

Вхождение переменной в область действия связывающего её квантора – связанное вхождение.

(подробнее о свободных и связанных вхождениях читайте выше)

Есть ещё другие определения, выбирайте то, что больше по душе, приведу их ниже.

Связанным вхождением предметной переменной х в формулу А будем называть вхождение предметной переменной х, находящееся в области действия квантора V или 3 в формуле А, за которым сразу же расположена буква х.

Свободным вхождением предметной переменной х в формулу А будем называть вхождение предметной переменной х, не находящееся в области действия квантора V или 3 в формуле А, за которым сразу же расположена буква х.

Тип переменной определяет множество значений, которые могут быть ей присвоены и операции, которые могут быть с нею произведены.

Свободные и связанные вхождения переменных определяются рекурсивно одновременно с type (x, f) - типом переменной x в формуле f и men (x, f) – множеством ссылок переменной x в f. И тип переменной type (x, f), и множество ссылок men (x, f) определены только в случае, если x имеет свободное вхождение в f (т.е. «x появляется в f свободно). Понятия свободы, связанности, типа и множества ссылок используются для определения класса разрешённых формул через ограничения на употребление различных связок.

Рисунок 3 – По поводу выражений