№1

Функция задана таблицей:

Вычислить по формуле Симпсона.

Решение:

1. Для использования формулы Симпсона необходимо найти, например, - для этого нужно решить задачу интерполяции для точки . Воспользуемся формулой Лагранжа.

2. Перенумеруем узлы так, чтобы точка лежала между узлам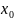и и , далее добавим узлы симметрично точке :

3. Запишем и рассчитаем интерполяционные многочлены Лагранжа 1-й, 2-й и 3-й степени при :

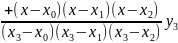
По факту для этой табличной функции достаточно рассчитать только , а вообще по канону методички нужен ; нет смысла считать все эти многочлены, нужен только один. Если в не подставлять конкретное значение , то получится функция, описывающая табличную (в случае с будет уже что-то другое, потому что в таблице квадратичная зависимость, а в будет кубическая).

4. Перепишем таблицу для :

5. Воспользуемся формулой Симпсона: , где

№2

Функция задана таблицей:

Вычислить по формуле трапеций.

Решение:

1. Отрезок разобьём на равных отрезка.

2. Воспользуемся формулой трапеций: , где

№3

Функция задана таблицей:

Вычислить по формуле правых и левых прямоугольников.

Решение:

1. Отрезок разобьём на равных отрезка.

2. Воспользуемся формулой левых прямоугольников:

3. Воспользуемся формулой правых прямоугольников:

4. Запишем формулу средних прямоугольников:

5. Получим интерполяционный многочлен в явном виде, воспользовавшись формулой Лагранжа. Перенумеруем узлы так, чтобы точка лежала между узлами и , далее добавим узлы симметрично точке :

6. Запишем и рассчитаем интерполяционный многочлен Лагранжа 2-й степени (возможно, попросят посчитать и 3-ю степень):

7. Воспользуемся формулой средних прямоугольников:

№4

Функция задана таблицей:

Решить задачу интерполяции в точке с использованием формулы Лагранжа. Выполнить 2 итерации и проверить полученную точность.

Решение:

1. Перенумеруем узлы так, чтобы точка лежала между узлами и , далее добавим узлы симметрично точке :

2. Запишем и рассчитаем интерполяционные многочлены Лагранжа 1-й и 2-й степени при :

3. Оценим погрешность вычислений:

№5

Функция задана таблицей:

Решить задачу интерполяции в точке с использованием формулы Ньютона. Выполнить 2 итерации и проверить полученную точность.

Решение:

1. Заполним таблицу конечных разностей:

(конечные разности второго порядка равны между собой, поэтому таблично заданную функцию можно представить многочленом второй степени)

2. Запишем первую формулу Ньютона: Эту формулу можно записать и в другом виде:

3. Рассчитаем интерполяционные многочлены Ньютона 1-й и 2-й степени при :

4. Оценим погрешность вычислений: Также погрешность можно рассчитать по приближённой формуле: При получим

№6

Функция интерполируется многочленом первой степени на отрезке . Оценить погрешность интерполяции на отрезке.

Решение:

1. Для интерполяции с помощью многочлена Лагранжа первой степени достаточно 2-х узлов: и . Пусть . Составим таблицу:

2. Найдём многочлен Лагранжа 1-й степени в явном виде:

3. Погрешность интерполяции определяется по формуле: В данном случае погрешность можно оценить следующим образом:

4. Добавим узел в точке , чтобы рассчитать , и составим таблицу:

5. Рассчитаем в явном виде:

6. Оценим погрешность в точке :

№7

Интерполируемая функция задана таблицей:

Найти интерполяционный многочлен путём решения системы линейных уравнений (используя основное свойство интерполяционного многочлена).

Решение:

1. Требуется найти - коэффициенты, зависящие только от узлов текущего значения ;

2. Запишем и решим систему уравнений:

3. 

4. 

5. 

6. 

7. Найдём :

8. Проверим правильность расчётов:

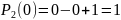
№8

Найти решение дифференциального уравнения в точке методом Эйлера*. Сделать 2 итерации и оценить точность. Начальные условия: .

Решение:

1. Решим дифференциальное уравнение: При : Можно решить дифференциальное уравнение иначе:

2. Пусть , на отрезке

3. По формуле Ньютона-Лейбница: Отсюда общий вид формулы Эйлера**:

4. Решим дифференциальное уравнение методом Эйлера на отрезке при :

5. Погрешность метода Эйлера:

*Метод Эйлера называется методом Рунге-Кутты 1-го порядка.

**В методе Эйлера используется допущение, что на интервале производная исходной функции постоянна и равна своему значению в точке . Отсюда по формуле прямоугольников или Отсюда выводится общий вид формулы Эйлера.

№12

Найти решение дифференциального уравнения в точке методом Рунге-Кутты 2-го порядка. Проделать 1 итерацию. Начальные условия: .

Решение:

1. Решим дифференциальное уравнение: При : Можно решить дифференциальное уравнение иначе:

2. Пусть , на отрезке

3. Вычисление значения искомой функции методом Рунге-Кутты 2-го порядка проводится в 2 этапа. Сначала вычисляют вспомогательную величину Затем значение производной искомой функции в точке используется для вычисления окончательного значения функции:

4. Пусть , на отрезке

5. Решим дифференциальное уравнение методом Рунге-Кутты 2-го порядка на отрезке при :

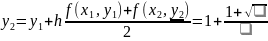
6. Погрешность метода Рунге-Кутты оценивается следующим образом: , где - порядок метода Рунге-Кутты. Эта формула также называется правилом Рунге.