Добавил:

lipton15 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

Программные средства моделирования СВЧ электронной компонентной базы

Файл:

курсачи / Kursovaya_Rabota_Saphonov_S_V_5201

.docx

Скачиваний:

Добавлен:

28.04.2022

Размер:

113.8 Кб

Скачать

☆

МИНОБРНАУКИ РОССИИ

Государственное образовательное учреждение

высшего профессионального образования

Санкт-Петербургский государственный электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

ФАКУЛЬТЕТ ЭЛЕКТРОНИКИ (ФЭЛ)

КАФЕДРА Радиотехнической электроники

КУРСОВАЯ РАБОТА (ПРОЕКТ)

По дисциплине: ПРОГРАММНЫЕ СРЕДСТВА МОДЕЛИРОВАНИЯ ЭЛЕКТРОННОЙ КОМПОНЕНТНОЙ БАЗЫ

На тему: Разработка модуля программы анализа электронного прибора

(указывается обобщенная тема)

Вариант № 16

Выполнил: Сафонов С.В. Группа: 5201

Преподаватель: Синев А.Е.

САНКТ-ПЕТЕРБУРГ

2019 г.

ЗАДАНИЕ на курсовую работу

По дисциплине: ПРОГРАММНЫЕ СРЕДСТВА МОДЕЛИРОВАНИЯ ЭЛЕКТРОННОЙ КОМПОНЕНТНОЙ БАЗЫ

Название курсовой работы:	Модуль расчёта потенциала от объёмного заряда методом интегральных уравнений.
Содержание работы:	Разработка алгоритма и С++ - программы расчёта потенциала внутри области с заданным объёмным зарядом.
Исходные данные:	Замкнутая поверхность, заданная набором плоских треугольников, и распределение заряда  внутри области, ограниченной этой поверхностью.
Результаты работы:	1. Программа расчёта потенциала от объёмного заряда методом интегральных уравнений. 2. Методика тестирования и отладки программы.
Литература:	1. Internet. 2. Моделирование полупроводниковых приборов и технологических процессов. Последние достижения. Под ред. Д. Миллера, М.: Радио и связь, 1989.

Теоретические выкладки

Для аналитического решения прямой задачи, т. е. расчета электрического поля по заданному распределению заряда в виде трех компонент вектора E или D, одного соотношения Error: Reference source not found недостаточно. Однако электрическое поле обладает очень важным свойством, которое можно использовать в дополнение к Error: Reference source not found и которое проявляется при вычислении работы электрических сил по перемещению заряда q в поле заряда q₀ вдоль произвольного контура l (рис. Error: Reference source not found).

При перемещении вдоль малого элемента контура dl под действием силы F элементарная работа dA определяется по формуле , в которой учтено, что вектор dl направлен вдоль касательной к контуру и при малых перемещениях dl совпадает с хордой dr и через dr обозначен не модуль вектора dr, а длина проекции данного вектора на направление радиуса-вектора r, т. е. положено, что dr – это изменение длины радиуса-вектора. Тогда .

Полная работа электрических сил при перемещении заряда q из точки a в точку b и не зависит от формы пути. Это общее свойство всех центральных сил.

Силы, работа которых не зависит от формы пути, называются консервативными силами.

Очевидно, что при перемещении заряда из b в a по любому контуру работа и потому работа консервативных сил по замкнутому контуру равна нулю: . (2.0)

Потенциалом называют такую функцию, разность значений которой в двух точках а и b равна взятой с обратным знаком работе сил электрического поля при переносе единичного положительного заряда из точки b в точку а: . (2.0)

Приведенное определение просто констатирует факт существования некоторой физической величины, которая обладает указанным нетривиальным свойством. Кроме того, из ( 2 .0) с неизбежностью следует, что потенциал определен лишь разностью своих значений в двух точках, т. е. потенциал в одной точке, например в a, определяется с точностью до постоянной (b): и для однозначного определения (a) необходимо каким-либо образом задать эту постоянную. Чаще всего точку b, являющуюся точкой отсчета потенциала, размещают либо в , либо на металлических поверхностях, соединенных с землей, и полагают, что (b)  0.

В случае поля точечного заряда ( 2 .0) преобразовывается к виду .

Учитывая, что при r_b вторые слагаемые в обеих частях равенства обращаются в нуль, для произвольной точки поля точечного заряда получим .

Воспользовавшись принципом суперпозиции и перейдя к произвольной системе координат, не связанной с каким-либо зарядом, можно показать, что для системы, образованной дискретным набором точечных зарядов, , где r_i =│r – r_i│ – расстояния от точек расположения точечных зарядов до произвольной точки поля, заданной своим радиусом-вектором r.

Если заряды распределены в пространстве непрерывно, то потенциал поля в произвольной точке а может быть найден интегрированием по всему объему, где имеются заряды, т. е. по координатам точек источников: . Здесь  – объемная плотность заряда, R – расстояние от точки а до произвольного элемента объема dV и произведение dV имеет смысл точечного заряда. В тех случаях, когда заряды распределены на поверхности проводников в очень тонком слое, имеет смысл говорить о поверхностном распределении заряда, и тогда потенциал может быть определен по формуле , где dS – элемент поверхности с поверхностной плотностью заряда .

О дним из наиболее важных примеров использования теоремы Грина является поиск общего вида решения уравнения Лапласа–Пуассона для неограниченного пространства, регулярного везде на конечном расстоянии и стремящегося к нулю на бесконечности. Это решение широко используется в практических задачах. Применим теорему Грина к функциям  и  в объеме V, ограниченном замкнутой поверхностью S (рис. Error: Reference source not found):

Пусть  – искомая функция, удовлетворяющая Error: Reference source not found, а  – функция вида , где , ,  – координаты текущих точек Q (точек истока), по которым ведется интегрирование, а х, y, z – координаты точки наблюдения Р, в которой ищется значение потенциала .

Код программы

// course_work.cpp: определяет точку входа для консольного приложения.

// формула n-го члена арифметической прогресии an=a1+d(n-1)

// подключаем заголовочные файлы

#include "stdafx.h" //служит для ускоорения процесса компиляции

#include <stdio.h>

#include <iostream> //неоюходимо для организации ввода-вывода

#include <math.h> //содержит математические функции

#include <clocale> // нужно для вывода кириллицы в консоли

#include <iomanip>

#include <cstdlib> //необходимо для функции system

using namespace std; // необходимо для потокового ввода-вывода данных

double s1,s2,s3,s4,s5,s6,fi_,E0; //значение с плавающей точкой

double M_PI = 3.14159265358979323846;

int main(void)

{

setlocale(LC_ALL,"Rus"); //кирилица в консоли

E0=8,85E-12; //д.э постоянная

//Ввод стороны куба (а) и разбиения (n), используем потоковый ввод-вывод

double a,n; //значение с плавающей точкой

cout << "Введите сторону куба а=";

cin >> a;

cout << "Введите значение разбиения n=";

cin >> n;

//Ввод координат точки с клавиатуры

double x,y,z; //значение с плавающей точкой

cout << "Введите координату x=";

cin >> x;

if(x<a)

{

cout << "Введите координату y=";

cin >> y;

if(y<a)

{

cout << "Введите координату z=";

cin >> z;

if(z<a)

{

//Ввод объемной плотности заряда с клавиатуры

double Sigma; //значение с плавающей точкой

cout << "Поверхностная плотность заряда Sigma=";

cin >> Sigma;

//Ввод относительной диэлектрической проницаемости с клавиатуры

double E; //значение с плавающей точкой

cout << "Относительная диэлектрическая проницаемость E=";

cin >> E;

double eps = E*E0;

//Рассчитываем шаг

double d; //значение с плавающей точкой для первого куба

d=a/n;

//Рассчитываем площадь минимальной ячейки

double dS; //значение с плавающей точкой

dS=d*d;

//Рассчитываем расстояния до точки, в которой определяется потенциал с помощью цикла for

double r1,r2,r3,r4,r5,r6,p1,p2,p3,p4,p5,p6; //значение координат с плавающей точкой для первого куба

double m1,m2,m3,m4,m5,m6,o1,o2,o3,o4,o5,o6;

double r11,r22,r33,r44,r55,r66;

for (int i=1; i<=n; i++)

{

for (int j=1; j<=n; j++)

{

r1=sqrt(((x-(1+(i-1)*2)*d/2)*(x-(1+(i-1)*2)*d/2)+(y-(1+(j-1)*2)*d/2)*(y-(1+(j-1)*2)*d/2)+z*z));

// используя формулу для n-го члена арифметической прогрессии определяем расстояние от первой

// грани до точки определения потенциала

r11=sqrt(((0.1*a+0.2*a*(i-1))-(1+(i-1)*2)*d/2)*((0.1*a+0.2*a*(i-1))-(1+(i-1)*2)*d/2)+((0.1*a+0.2*a*(j-1))-(1+(j-1)*2)*d/2)*((0.1*a+0.2*a*(j-1))-(1+(j-1)*2)*d/2)+0.1*a*0.1*a);

p1=Sigma*dS/(4*M_PI*E0*E*r1); // считаем потенциал

m1=Sigma*dS/(4*M_PI*E0*E*r11);

o1=m1*dS/(4*M_PI*r11*0.1*a);

s1+=p1+o1; // сложение совмещённое с присваиванием s1=s1+p1

}

for (int i=1; i<=n; i++)

{

for (int j=1; j<=n; j++)

{

r2=sqrt(((x-(1+(i-1)*2)*d/2)*(x-(1+(i-1)*2)*d/2)+(y-(1+(j-1)*2)*d/2)*(y-(1+(j-1)*2)*d/2)+(z-a)*(z-a)));

// используя формулу для n-го члена арифметической прогрессии определяем расстояние от второй

// грани до точки определения потенциала

r22=sqrt(((0.1*a+0.2*a*(i-1))-(1+(i-1)*2)*d/2)*((0.1*a+0.2*a*(i-1))-(1+(i-1)*2)*d/2)+((0.1*a+0.2*a*(j-1))-(1+(j-1)*2)*d/2)*((0.1*a+0.2*a*(j-1))-(1+(j-1)*2)*d/2)+0.1*a*0.1*a);

p2=Sigma*dS/(4*M_PI*E0*E*r2); // считаем потенциал

m2=Sigma*dS/(4*M_PI*E0*E*r22);

o2=m2*dS/(4*M_PI*r22*0.1*a);

s2+=p2+o2; // сложение совмещённое с присваиванием s2=s2+p2

}

for (int i=1; i<=n; i++)

{

for (int j=1; j<=n; j++)

{

r3=sqrt((x*x+(y-(1+(i-1)*2)*d/2)*(y-(1+(i-1)*2)*d/2)+(z-(1+(j-1)*2)*d/2)*(z-(1+(j-1)*2)*d/2)));

// используя формулу для n-го члена арифметической прогрессии определяем расстояние от второй

// грани до точки определения потенциала

r33=sqrt((0.1*a*0.1*a+((0.1*a+0.2*a*(i-1))-(1+(i-1)*2)*d/2)*((0.1*a+0.2*a*(i-1))-(1+(i-1)*2)*d/2)+((0.1*a+0.2*a*(i-1))-(1+(j-1)*2)*d/2)*((0.1*a+0.2*a*(i-1))-(1+(j-1)*2)*d/2)));

p3=Sigma*dS/(4*M_PI*E0*E*r3); // считаем потенциал

m3=Sigma*dS/(4*M_PI*E0*E*r33);

o3=m3*dS/(4*M_PI*r33*0.1*a);

s3+=p3+o3; // сложение совмещённое с присваиванием s3=s3+p3

}

for (int i=1; i<=n; i++)

{

for (int j=1; j<=n; j++)

{

r4=sqrt((x-a)*(x-a)+(y-(1+(i-1)*2)*d/2)*(y-(1+(i-1)*2)*d/2)+(z-(1+(j-1)*2)*d/2)*(z-(1+(j-1)*2)*d/2));

// используя формулу для n-го члена арифметической прогрессии определяем расстояние от второй

// грани до точки определения потенциала

r44=sqrt(0.1*a*0.1*a+((0.1*a+0.2*a*(i-1))-(1+(i-1)*2)*d/2)*((0.1*a+0.2*a*(i-1))-(1+(i-1)*2)*d/2)+((0.1*a+0.2*a*(i-1))-(1+(j-1)*2)*d/2)*((0.1*a+0.2*a*(i-1))-(1+(j-1)*2)*d/2));

p4=Sigma*dS/(4*M_PI*E0*E*r4); // считаем потенциал

m4=Sigma*dS/(4*M_PI*E0*E*r44);

o4=m4*dS/(4*M_PI*r44*0.1*a);

s4+=p4+o4; // сложение совмещённое с присваиванием s4=s4+p4

}

for (int i=1; i<=n; i++)

{

for (int j=1; j<=n; j++)

{

r5=sqrt((x-(1+(i-1)*2)*d/2)*(x-(1+(i-1)*2)*d/2)+y*y+(z-(1+(j-1)*2)*d/2)*(z-(1+(j-1)*2)*d/2));

// используя формулу для n-го члена арифметической прогрессии определяем расстояние от второй

// грани до точки определения потенциала

r55=sqrt(((0.1*a+0.2*a*(i-1))-(1+(i-1)*2)*d/2)*((0.1*a+0.2*a*(i-1))-(1+(i-1)*2)*d/2)+0.1*a*0.1*a+((0.1*a+0.2*a*(i-1))-(1+(j-1)*2)*d/2)*((0.1*a+0.2*a*(i-1))-(1+(j-1)*2)*d/2));

p5=Sigma*dS/(4*M_PI*E0*E*r5); // считаем потенциал

m5=Sigma*dS/(4*M_PI*E0*E*r55);

o5=m5*dS/(4*M_PI*r55*0.1*a);

s5+=p5+o5; // сложение совмещённое с присваиванием s5=s5+p5

}

for (int i=1; i<=n; i++)

{

for (int j=1; j<=n; j++)

{

r6=sqrt((x-(1+(i-1)*2)*d/2)*(x-(1+(i-1)*2)*d/2)+(y-a)*(y-a)+(z-(1+(j-1)*2)*d/2)*(z-(1+(j-1)*2)*d/2));

// используя формулу для n-го члена арифметической прогрессии определяем расстояние от второй

// грани до точки определения потенциала3

r66=sqrt(((0.1*a+0.2*a*(i-1))-(1+(i-1)*2)*d/2)*((0.1*a+0.2*a*(i-1))-(1+(i-1)*2)*d/2)+0.1*a*0.1*a+((0.1*a+0.2*a*(i-1))-(1+(j-1)*2)*d/2)*((0.1*a+0.2*a*(i-1))-(1+(j-1)*2)*d/2));

p6=Sigma*dS/(4*M_PI*E0*E*r6); // считаем потенциал

m6=Sigma*dS/(4*M_PI*E0*E*r66);

o6=m6*dS/(4*M_PI*r66*0.1*a);

s6+=p6+o6; // сложение совмещённое с присваиванием s6=s6+p6

}

fi_=s1+s2+s3+s4+s5+s6; //финальное значение потенциала

cout << fi_ <<endl;

}

system("pause"); //пауза, чтобы консоль не закрылась

return 0; //возвращаем нулевое значение

}

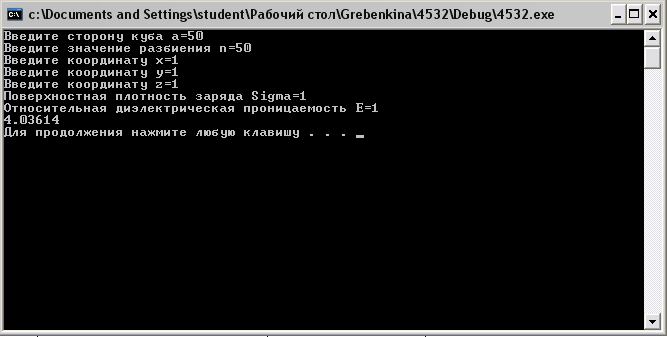
Рисунок 1 – Пример работы программы

2. Тестирование

Тестирование программы заключается в проверке вычисления потенциала при разном разбиении. Её результаты представлены в таблице №1.

Таблица №1

Сторона куба а	50
Координата X	1
Координата Y	1
Координата Z	1
Поверхностная плотность заряда	1
Относительная д/э проницаемость	1
Количество разбиений	Потенциал
50	4,03614
100	4,03441
150	4,03409
200	4,03398
250	4,03393
300	4,03391
350	4,03389
400	4,03388
450	4,03387
500	4,03387
550	4,03385
600	4,03386
650	4,03386
700	4,03386
800	4,03386
900	4,03385
1000	4,03385

Вывод:

Исходя из результатов расчетов можно заметить, что при увеличении числа разбиений потенциал стремится к определенному значению.

Список литературы.

1. Internet.

2. Моделирование полупроводниковых приборов и технологических процессов. Последние достижения. Под ред. Д. Миллера, М.: Радио и связь, 1989.

Соседние файлы в папке курсачи

#
28.04.2022181.25 Кб6kursach.doc
#
28.04.2022137.45 Кб7Kursach.docx
#
28.04.2022125.99 Кб7Kursovaya.docx
#
28.04.20222.7 Mб11Kursovaya_POtapova.docx
#
28.04.2022180.12 Кб8Kursovaya_Rabota_PSM_EKB_Maltsev_4201.docx
#
28.04.2022113.8 Кб7Kursovaya_Rabota_Saphonov_S_V_5201.docx
#
28.04.202250.99 Кб6Kursovaya_rabota_Tikhonov_P_M.docx
#
28.04.2022117.76 Кб6Kursovaya_rabota_Titulny_list__zadanie_2021.doc
#
28.04.2022194.96 Кб5kursovaya_S.docx
#
28.04.2022120.92 Кб4KursVork.docx
#
28.04.202271.49 Кб6Kurs_Otc (1).docx