Методическое пособие 719

,

< , >

=

1

+∞

( ) ( ) −

2

2 2

1

√2

−∞

=

+∞

2

|| ||

( ( ))2

−

= < , >

2 2

Так как

√2

−∞

+ ) + ( + )

= cos

= ( + ) (

+ ) = (

Найдем линейные оценки

+ ) ≈ (

+ )

(

(

+ ) ≈

(2.1)

Так чтобы

≈ +

+

[cos( + ) −

−

] →

,

[cos(

+ ) − ] →

То

=

( )

Где

=

( ), = ( ),

и

и

есть вещественные числа и не зависят от

есть

||cos( + ) − − || →

Другими словами

||cos( + ) − ||

→

Где

Рассмотрим пространство

– множество всех многочленов со степенью

=

не выше чем

[3]

0

=

1

= +

наша задача

и

т.ч.

0

1

Множество

есть подпространство множества

[6], Таким образом

0

0

эквивалентна задаче о нахождении

+ ) −

( )||

|| (

+ ) −

( )||

=

inf

|| (

|| (

+ ) −

( )||

=

0 0

|| (

+ ) −

( )||

inf

1

1 1

1

пространство

1 0

есть базиз

в

0

и

пространство

есть

Гильбертово

Так

как

[6, 3], мы можем применить

метод неопределенных

Следовательно

< 1, ( + ) − >= 0

(2.2)

коэффицентов

√21

∫−∞+∞ ( ( + ) − ) −

222

= 0

√21

∫−∞+∞ ( + ) −

222

− √2 ∫−∞+∞ −

222

= 0

Так как

√21

∫−∞+∞ −2 22

= 1 [8]

120

=

1

+∞

( + )

−

2

=

1

+∞

( ( ) ( ) − ( ) ( )) −

2

2 2

2 2

√2

−∞

+∞

√2

−∞

+∞

2

=

1

( ) ( ) −

2

−

1

( ) ( )

−

2 2

2 2

√2

−∞

+∞

2

√2

−∞

+∞

2

= ( )

( ) −

−

( )

( ) −

Так как

2 2

2 2

√2

−∞

√2

−∞

Следовательно ( ) −22

∫−∞+∞ ( ) −22

= 0

=

функция

( )

2

нечётная

2

[5]

√2

∫−∞

2 22

(

)

− 22

( )

+∞

−

=

(2.3)

Векторы

1,

2

1

образуют базис

+∞

1

в

. Кроме того

Следовательно

< 1, >=

1

−2 2

= 0

1

следовательно

система

√2

−∞

{1, }

образует

базис

в

[6],

векторов

Можем

< 1, ( + ) −

>= 0

(2.4)

< , ( + ) −

>= 0

(2.5)

Решим уравнение

= cos( )

заметить что уравнения (2.4) и (2.2) одинаковы, следовательно

2

(2.5)

1

− 2

(2.6)

+∞

2

< , (

+ ) − >=

( (

+ ) − ) −

=

2 2

1

+∞

√2 2

−∞

+∞

2

( + ) −

−

2 −

= 0

Так как

2 2

2 2

√2

−∞

1

+∞

√2

−∞

2

2 −

= 2

Следовательно

2 2

√2

−∞

2

2

=

1

+∞

( + ) −

=

2 2

1

+∞

√2

−∞

1

+∞

2

=

( ) ( ) −

2

−

( ) ( )

−

=

2 2

2 2

√2

−∞

+∞

2

√2

−∞

+∞

2

=

( )

( ) −

−

( )

( ) −

2 2

2 2

√

2

−∞

√

2

−∞

( ) −2 2

∫−∞+∞ ( ) −2 2 = 0

Так как функция

2

нечётная

2

121

Следовательно

2

= − ( )

+∞

( ) −

2

2 2

= − √2 3

∫−∞

( )

2

√2

−∞

2

= −( ) −

( )

+∞

−

22

2

(2.7)

= sin

= (

+ ) (

+ ) = ( + ) + (

+ )

Таким образом все коэффиценты в (2.1) найдены. Повторим процесс для

(

+ ) ≈ (

+ )

Найдём линейные оценки

( + ) ≈

Аналогично (2.2)

≈

+

+

(2.8)

Следовательно

1

< 1, ( + ) − >= 0

(2.9)

+∞

( ( + ) − ) −

2

= 0

√

2 2

−∞

2

+∞

2

1

+∞2

( + ) −

−

−

= 0

2 2

2 2

2

2

√21

∫−∞+∞ −2 2

= 1

+∞

√2 −∞ Therefore, since

+∞

√2

−∞2

[8]

1

1

=

( + ) −

=

( ( ) ( ) + ( ) ( )) −

2 2

2 2

√2

−∞

−2 2

√2

−∞

−2 2

− 2

( )

+∞

( )

+∞

=

2

2

2

=

√2

( )

+

√2

( )

= (

)

−∞

−∞

(2.10)

Таким образом

= ( ) − 22

Аналогично имеем

< 1, ( + ) −

>= 0

(2.12)

Так как уравнения (2.9)

< , (

+ ) − >= 0

(2.11)

Решим уравнение

(2.12)

= ( ) − 22

(2.13)

и (2.11) одинаковы, следовательно

< , (

+ ) − >=

1

+∞

( (

+ ) − ) −

2

=

2 2

1

+∞

√2 2

−∞

+∞

2

2

(

+ )

−2 2

−

−2 2

= 0

√2

√2

−∞

−∞

Следовательно

122

2

=

1

+∞

(

+ ) −

2

=

+∞

2 2

2

1

√2

−2∞

1

+∞

=

( ) ( ) −2 2 +

( ) ( ) −2 2 =

√2

−∞+∞

2

√2 +∞

−∞

2

−

2

=

( )

( )

−2 2

+

( )

( )

−2 2

= (

)

2

√2

√2

−∞

−∞

Таким образом мы

= ( )

Следовательно

2

(2.14)

доказали теорему.

−

2

Теорема 2. Оценки

=

+

+

Будут иметь

=

+

+

− ]

[

− ]

линейных оценок.

[

наименьшие значения для

и

среди

Теперь же

=

=

+

Представив в матричном виде

− ( )

+

) =

( − ) = (

вычтем

и вычислим ковариационную матрицу

0

− ( )

0

=

0

=

0

2

( − )2

2

2

Подставив полученные результаты имеем

2

2

2

2

22

2

2

0

(

)

−

− (

)

−

0

2

(

)

−

(

)

−

( )

−

2

( ) −22

− ( ) −

2

( )

−

2

=

2

2

02

( − ) = 2

−

2

−2 2

(2.15)

3.

0

(1.4) является частным случаем формулы

Нетрудно

заметить,

что

оценка

(2.15)когда значение

2

близка к нулю

Приближение в сферических системах координат.

Рассмотрим множество функций

− 22

− 22

( , ) = {

|

. .

(

2

)

∫−∞

∫−∞

( ( , ))

< ∞}

2

2 1

Это1

2 множество

+∞

+∞

2

образует

линейное

пространство.

Определим

также

скалярное произведение и норму

1

+∞

2

+∞

2

, ( 1

, 2)

< , >

=

−2 22

( , ) ( , ) −2 12

(

2 1 2

−∞

−∞

>

Применив тот

,

)

|| ||( , )

= < ,

же метод1

вычислений2 1 2

,

получается оптимальная линейная

оценка и следующая ковариационная матрица

123

−( η+ δ)

0

2

2

0

(3.1)

2

(

− H

) =

3

0

2

2

−( η+ δ)

0

2

где

2

2

3

0

0

−δ

cos cos

− cos

−

2

2

3 = sin

cos cos

−

Нетрудно

sin

0

что

является

частным

случаем

также

заметить,

формула (1.5)

формулы (3.1) когда значение

2

2

близка к нулю.

4. Практическое

наблюдение при полярных координатах.

( η + δ )

Ковариационные матрицы (1.4) и (2.15) были использованы при

алгоритме фильтрации Kальмана на компьютерной симуляции при различных

значениях

||

где .

||

−

результат

данной

Далее

можете видеть

компьютерной симуляции,

=

при использовании ковариационной матрицы (1.4), а

2

–

при

1

использовании (2.15)

1 > 0

Таким образом, если

-

то новая ковариационная матрица выдает

лучший результат и

наоборот.

2

Рис. 1. = 0.01 1.

Рис. 2. = 0.1

124

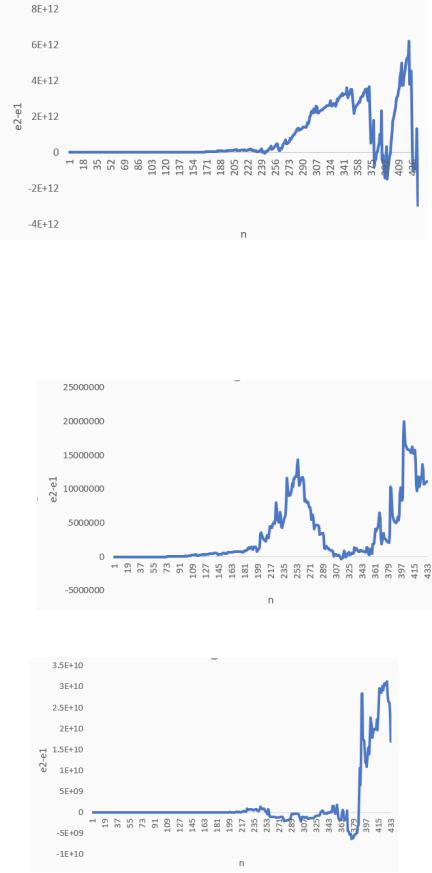
Рис. 3. = 0.5

Как видно из полученных результатов, новая ковариационная матрица в большинстве случаев лучше прежней.

6. Практическое наблюдение при сферических системах координат.

Рис. 4. = 0.05 = 0.05

Рис. 5. = 0.1 = 0.2

125

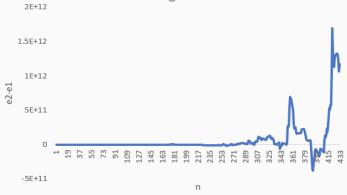
Рис. 6. = 0.4 = 0.3

В этом случае также видно улучшение алгоритма.

Литература

1.Kalman, R.E. (1960). "A new approach to linear filtering and prediction problems". Journal of Basic Engineering. 82 (1): 35–45. doi:10.1115/1.3662552. Archived from the original (PDF) on 2008-05-29. Retrieved 2008-05-03.

2.Kalman, R.E.; Bucy, R.S. (1961). "New Results in Linear Filtering and Prediction Theory"

3.Hakobyan Y.R. Basics of Numerical Analysis (2005)

4.Ramachandra K.V. (2000) "Kalman Filtering Techniques for Radar Tracking" 1st Edition

5.Ahlfors L. Complex Analysis, 3 ed. (McGraw-Hill, 1979).

6.Alan. F. Beardon Algebra and Geometry by 1st Edition (Combridge University Press)

7.Hazewinkel, Michiel, ed. (2001) [1994], "Covariance matrix", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4

8.Gmurman V.E. (1968) Fundamentals of Probability Theory and Mathematical Statistics

Российско-Армянский (Славянский) университет, Армения

УДК 330.42

Е.А. Хохлова

ПРИМЕНЕНИЕ ЭКОНОМИКО-МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ДЛЯ ЦЕЛЕЙ УПРАВЛЕНИЯ ДЕБИТОРСКОЙ ЗАДОЛЖЕННОСТЬЮ (НА ПРИМЕРЕ ООО «РОБЕРТ БОШ»)

Аннотация: Настоящая статья представляет собой исследование по вопросу эффективного управления дебиторской задолженностью с применением

126

экономико-математического моделирования. Для целей эффективного управления в данной работе были разработаны: шкала штрафов за дебиторскую задолженность, шкала вознаграждений для дебиторов, а также была разработана сама модель, позволяющая наиболее удобным способом управлять дебиторской задолженностью. Данная модель наглядно демонстрирует преимущество для контрагентов в предварительной оплате в связи с введением положения о шкале вознаграждений. Имитационная модель была разработана для предприятия

ООО «Роберт Бош», но она имеет практическое значение и для других компаний, работающих с дебиторской задолженностью. В целом, использование данной модели удобно как для специалистов компании, на балансе которой находится дебиторская задолженность, так и для компании-должника, ведь макет моделирования можно представлять контрагентам в качестве мотивационной меры, так как контрагенты смогут в режиме реального времени видеть основные преимущества и недостатки для своего положения. По моему мнению, данная модель точно позволит сократить дебиторскую задолженность, тем самым, позволит увеличить положительный денежный поток компании.

Ключевые слова: моделирование, имитационная модель, дебиторская задолженность, экономико-математическое моделирование

Тенденция присутствия и наращивания дебиторской задолженности приводит к фактической иммобилизации части текущих активов, что является причиной снижения финансовой устойчивости и платежеспособности предприятий [1]. В этой связи актуальной проблемой является разработка мер по управлению дебиторской задолженностью.

Целью настоящей статьи является разработка имитационной модели [2], с помощью которой компании смогут управлять дебиторской задолженностью. Для осуществления данной цели необходимо выполнить ряд задач:

1.Разработать шкалу штрафов за дебиторскую задолженность;

2.Разработать шкалу вознаграждений для дебиторов;

3.Проанализировать полученные данные.

В качестве анализируемого предприятия была выбрана компания ООО

«Роберт Бош», относящаяся к категории «Производство, торгово-произ- водственные компании». Были представлены некоторые данные бухгалтерского баланса ООО «Роберт Бош» за 2015-2017 гг., а также рассчитаны: показатель средней дебиторской задолженности, коэффициент оборачиваемости дебиторской задолженности и период оборота дебиторской задолженности.

Таким образом, в исследовании были разработаны: шкала штрафов за дебиторскую задолженность, шкала вознаграждений для дебиторов, а также проанализированы полученные результаты и разработана имитационная модель, позволяющая эффективно управлять дебиторской задолженностью [3].

127

Литература

1.Colander D. The Complexity Revolution and the Future of Economics // Middlebury College Working Paper Series 0319 / Middlebury College, Department ofEconomics. 2003. P. 4.

2.Мицель, А.А. Имитационное моделирование экономических процессов

вExcel / А.А. Мицель, Е.Б. Грибанова. – Юрга: Изд-во ЮТИ (филиал) ТПУ, 2016. –115 с.

3.Stulz R. Risk Management Failures: What Are They and When Do They Happen?//Working paper//SSRN, 2008. October.

ФГАОУ ВО «Самарский национальный исследовательский университет имени академика С.П. Королёва», Россия

УДК 519.176:178

А.А. Котенко

ОПТИМИЗАЦИОННЫЕ ХАРАКТЕРИСТИКИ ПЕРЕМЕЩЕНИЙ ПО ВЕРШИНАМ ОРГРАФОВ С РАЗМЕЧЕННЫМИ ДУГАМИ

Введение. Рассмотрим неориентированный граф G(V,R) с множеством V вершин и множеством R размеченных рёбер. Метки рёбер – вещественные числа. Неотрицательные метки рёбер интерпретируем как расстояния между инцидентными вершинами, время перемещения между ними, стоимость такого перемещения и т.п. Построим дискретный конечный автомат K, оптимизирующий соответствующие метрические, временные и т.п. затраты на перемещения между группами вершин графа G. Целевые вершины представим входным алфавитом. Пример входного алфавита A – варианты попыток проникновения на защищаемый объект в дискретном времени. Выходной алфавит отсутствует. Множество Q состояний автомата K – размещение роя роботов-охранников в вершинах графа G.

В качестве начальной модели объекта возьмём прямоугольник из квадратных ячеек. Пример – размещение помещений в здании. Ограничимся следующим вариантом проникновения нарушителей – нарушители появляются поодиночке в любом наборе ячеек. Обычное жизненное ограничение – нарушители проникают на объект через периметр прямоугольника. Роль периметра играют внешние стены здания. Примем, что нейтрализация нарушителя производится мгновенно, как только любой робот-охранник роя переместится в квадрат с нарушителем. Считаем, что других затрат на нейтрализацию нарушителя (ликвидация, охрана и т.п.) нет.

Разрешим перемещение роботов между любыми ячейками объекта за один такт времени, однако учтём суммарные затраты на перемещение роя, за-

128

x 1, X

висящие от расстояния между ячейками. Минимизируем транспортные затраты на перемещение группы роботов-охранников роя с помощью алгоритмов решения транспортной задачи линейного программирования. Построим дизъюнктивную форму, реализующую оптимальную стратегию роя роботов в зависимости от стратегии поведения группы нарушителей.

Конкретные приложения охватывают задачи распределения такси между заказчиками с учётом актуального размещения такси в узлах городской застройки и случайного характера вызовов. Другой пример – выезд групп на ремонт аварий, происходящих в разных узлах энергосетей, сетей водоснабжения и т.д.

Постановка задачи. Пусть охраняемая территория – прямоугольник Z, разбитый на X×Y одинаковых квадратов mxy:

; y 1,Y ; X ,Y

– индексация ячеек представлена в таблице.

Под вариантом попытки проникновения понимаем появление одиночных нарушителей в любом наборе квадратов mxy. Пусть максимальное число нарушителей N в течение одного такта нападения меньше общего числа квадратов XY. Считаем, что в одном квадрате mxy не появится более одного нарушителя, так что одного робота-охранника достаточно для очистки квадрата от нарушителей.

Индексация ячеек области Z

m11	m12	m13	m14	…	m1,Y–1	m1,Y
m21	m22	m23	m24	…	m2,Y–1	m2,Y
m31	m32	m33	m34	…	m3,Y–1	m3,Y
…	…	…	…	…	…	…
mX–1,1	mX–1,2	mX–1,3	mX–1,4	…	mX–1,Y–1	mX–1,Y
mX,1	mX,2	mX,3	mX,4	…	mX,Y–1	mX,Y

На входе автомата K(A,Q) получим любую последовательность символов алфавита A, описывающую появление нарушителей в нескольких ячейках защищаемой территории Z в последовательные такты времени.

Начальным состоянием q1 автомата K(A,Q) считаем расположение всех M≥N роботов роя по одному в квадратах mxy с наименьшей суммой индексов x+y. Пример начального размещения роя роботов.

Потребуем, чтобы в дальнейшем в каждой ячейке области Z находилось не более одного робота. Большего числа охранников для нейтрализации нарушителей в одной клетке не требуется. С другой стороны, перемещение лишнего охранника в клетку, в которой уже имеется охрана, приведёт к росту транспортных затрат.

Нейтрализацией нарушителя, появившегося в такте времени tk в квадрате mxy, считаем перемещение любого робота роя в этот квадрат в следующем такте времени tk+1. Если в квадрате с нарушителем в момент tk уже находится робот-

129