Учебное пособие 1053

2.Изменение целевой функции:

−2x1 + x2 −3x3 −4x4 ≤ 3 ,

−x1 − x2 + x3 − x4 =1,

2x1 +3x2 + x3 − x4 ≥ 2, x j ≥ 0, j =1,4 ,

f (x) = −5x1 − x2 + x3 −7x4 → max . 3,4. Замена неравенств в ограничениях равенствами:

− 2x1 + x2 −3x3 −4x4 + x1ä = 3,

− x1 − x2 + x3 − x4 =1,

2x1 +3x2 + x3 − x4 − x3д = 2,

x j ≥ 0, j =1,4 ,

x1д ≥ 0, x3д ≥ 0,

f (x) = −5x1 − x2 + x3 −7x4 → max .

Это окончательный вид ЗЛП.

Заметим, что в соответствующем примере есть первая и третья дополнительные переменные. Для удобства номер дополнительной переменной соответствует номеру строки, в которой она присутствует.

В дальнейшем почти всегда ЗЛП будут рассматриваться только в канонической форме.

1.4. Базисное решение ЗЛП

Рассмотрим ЗЛП в каноническом виде.

	Ax = b,	(1.4.1)
	x ≥ 0,
		, m < n .
	f (x) = cT x → max , где A
	m×n

Будем считать, что rang(A) = m , то есть матрица А имеет m линейно независимых столбцов. Допустимое решение x = (x1, x2 , ... , xm ,0,0), x G называется базисным решением или опорным планом, если положительным значениям xi соответствуют линейно независимые столбцы матрицы А.

Базисное решение имеет не больше, чем m положительных компонент. Если число положительных компонент равно m, то решение называется невырожденным, и соответствующие столбцы матрицы А образуют базис в m-мерном пространстве. Если число положительных компонент меньше m, то решение называется вырожденным. Тогда, чтобы получить базис, к тем столбцам, которые соответствуют положительным компонентам, надо добавить столбцы с нулевыми компонентами.

Сформулируем без доказательства.

11

Утверждение 1: Если ЗЛП разрешима, то для нахождения оптимального решения достаточно перебрать только базисные решения, число которых ко-

нечно и не превосходит Сnm .

Рассмотрим сначала способ перестроения базисного решения системы Ax = b без условия неотрицательности.

Пусть матрица А имеет вид

= ( ~),

A E | A

где Е – единичная матрица.

Обозначим через IB множество номеров единичных столбцов матрицы А

и через I

~

множество остальных номеров столбцов. Вектор X представим в ви-

A

x

B

, где

x

= (x ),

i I

и x~

= (x ),

i I ~

. Вектор cT представим

де x =

x

~

B

i

B

A

i

A

A

в виде c

T

=

(c

T

T

B

, c~ ). Тогда система примет вид

A

~

xB + Ax~ = b .

A

Если положить x~

= 0, то получим базисное решение

b

x =

.

A

0

Будем получать новое базисное решение, заменяя один из базисных

столбцов на столбец, ранее принадлежащий I ~ . Это можно сделать с помощью

A

алгоритма Жордана-Гаусса.

Пусть выбрано k I ~ (номер столбца, который будет вводиться в базис)

A

и alk - направляющий элемент.

Шаг 1: l-строка делится на направляющий элемент.

В новой итерации эта строка будет иметь номер k.

			akjí	= ali / alk =θl ,
			xkí = xl / alk =θ ,
	Шаг 2:	Для i <> k		alk ≠ 0 .
			aijí = aij − aikθj ,
	Шаг 3:		xií = xi −aikθ .
			I Bí	= (I B\{l}) {k},
		í	= (I	~\{k}) {l}.
		I ~
		A		A

1.5. Перестроение базисного решения ЗЛП

Алгоритм Жордана-Гаусса не учитывает условия неотрицательности переменных. Для того чтобы это условие было учтено, надо выбирать k, а также alk так, чтобы условие неотрицательности сохранилось.

12

Так как ЗЛП рассматривается в канонической форме, то начальное базис-

ное решение x = b - неотрицательно.

0

Заметим, что если столбец Ak ≤ 0 , то его нельзя вводить в базис, так как

при любом выборе направляющего элемента alk	xkí = xl / alk < 0, поэтому для вве-
дения в базис необходимо выбирать столбец Ak , такой, что существует àik > 0.
Кроме того, как следует из алгоритма	Жордана-Гаусса, для i <> k

xií = xi −aikθ . Следовательно, необходимо выбрать θ таким образом, чтобы выполнилось условие: xi −aikθ ≥ 0 для всех i <> k .

Если aik ≤ 0 , то xií ≥ 0 для любого θ > 0 .

Если aik > 0, то существует максимальное θ , при котором xií ≥ 0. Его

можно найти по правилу θ = mina >0 (xi /aik ) = xl /alk .

ik

Алгоритм перестроения базисного решения ЗЛП

Пусть определен столбец с номером k, подлежащий введению в базис. Шаг 1: Определить l (номер выводимого столбца) по правилу

θ = minaik >0 (xi / aik ) = xl / alk .

Шаг 2: Переход к алгоритму Жордана-Гаусса.

Шаг 3: Вычислить значение целевой функции по формуле f (x) = cBT xB .

Из рассмотренного выше алгоритма следует, что перебрав с его помощью все базисные решения можно найти оптимальную точку.

Пример 1.4. Дана ЗЛП в канонической форме. Требуется найти оптимальное решение с помощью перебора базисных решений.

2x1 + x2 − x3 + x4 = 3; x1 + x2 + 2x3 + x5 = 5; xi ≥ 0, i =1,5,

f (x) = 5x1 + 2x2 − x3 −2x4 + x5 → max .

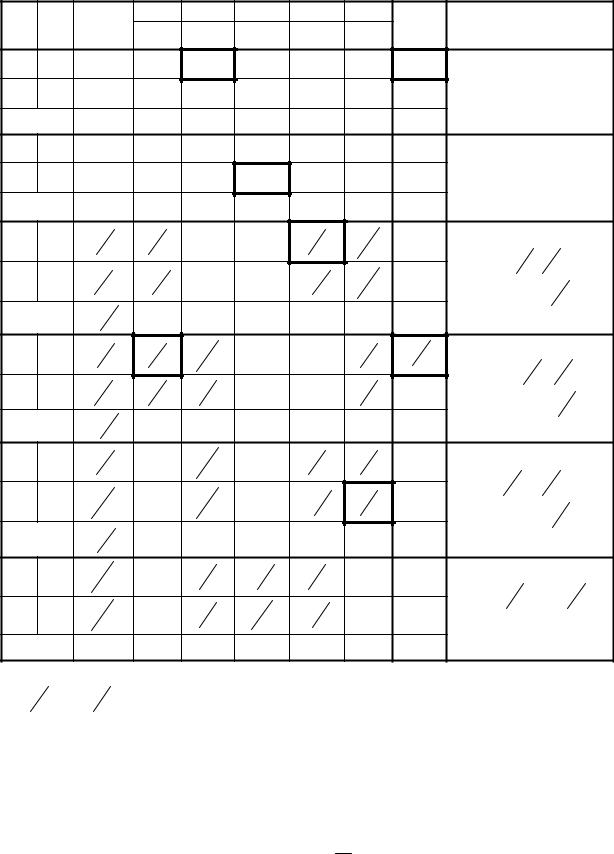
Решение. Оформим решение задачи в виде таблицы (табл. 1.4.). В первом столбце поместим текущие базисные переменные, во втором - их коэффициенты в целевой функции, в третьем - базисные координаты текущей точки xB . Далее пе-

реписываем элементы матрицы aij , помещая над каждым столбцом коэффициент

соответствующей переменной в целевой функции. Последний столбец предназначается для определения значения θ . В последней строке под xB записывается значение целевой функции, остальные клетки этой строки пока не заполнены.

13

										5		2		-1	-2			1						Таблица 1.4
B	cB			xB																θ	Базисное решение
										A1		A2		A3	A4			A5
x4		-2		3						2		1		-1	1			0		3		x	1	= (0,0,0,3,5)
x5		1		5						1		1		2	0			1		5
																							f (x1) = −1
f (x)				-1
x2		2		3						2		1		-1	1			0				x2		= (0,3,0,0,2)
x5		1		2						-1		0		3	-1			1
																								f (x2 ) = 8
f (x)				8
x2		2		113						53		1		0	23			1	3		x3	= (0,11						3		,	2		3	,0,0)
x3		-1		23						−13		0		1	−13			13
																							f (x3 ) =								20			3
f (x)			− 20
							3
x4		-2		11		2				5	2	3	2	0	1			1	2	115	x4	= (0,0,					5		2		,11				2		,0)
x3		-1		52						12		12		1	0			12		5
																						f (x			4	)		= −				27				2
f (x)			−	27
							2
												3
x1		5		115						1			5	0	25			15			x5	= (115 ,0,75 ,0,0)
x3		-1		7						0		1		1	− 1			2
					5								5			5			5				f (x			5	) =				48			5
f (x)			48
						5
				3
x1		5			2					1		12		−12	12			0			x	6 = (3				2		,0,0,0,								7		2	)
x5		1		72						0		12		52	−12			1
																								f (x6 ) =11
f (x)				11
Перебраны										все		базисные			точки,		и		оптимальной				точкой											является
x6 = (3	2	,0,0,0,		7	2			)	со значением					f (x6 ) =11.
												Лабораторнаяработа №2
ДанаЗЛП:													− x1 + 2x2 − x3 + x4 ≤ 2,
													bx1 + x2 + x3 − 2x4 ≤12,
													2x1 + cx2 + 4x3 + 2x4 ≤ 6,
														xi	≥ 0, i =1,4 ,
													f (x) = x1 − x2 − x3 + ax4					→ max .
															14

В табл. 1.5. приведены варианты значений параметров a, b, c.

Таблица 1.5

	a	b	c		a	b	c		a	b	c		a	b	c
1	2	3	-1	6	5	2	3	11	2	1	2	16	3	3	1
2	3	1	1	7	4	3	6	12	3	3	4	17	4	1	2
3	4	2	-1	8	6	1	5	13	5	2	-1	18	3	1	0
4	7	2	3	9	2	2	2	14	7	1	5	19	4	1	3
5	8	3	4	10	5	3	7	15	6	3	8	20	5	2	6

Необходимовыполнитьследующиезадания:

1.Привести ЗЛП к канонической форме.

2.С помощью алгоритма перестроения базисного решения ЗЛП найти четыре различных базисных решения и выбрать среди них наилучшее.

2. Симплекс-метод

Как было показано выше, с помощью перебора базисных решений можно получить оптимальное решение, если задача разрешима.

Заметим, что число базисных решений хотя и конечно, однако может быть весьма большим, при больших размерах задачи. Поэтому если имеется некоторая базисная точка, то хотелось бы знать:

1.Не является ли она оптимальной и если это так, то просмотр остальных точек не целесообразен;

2.Не является ли задача неразрешимой из-за неограниченности целевой функции. В этом случае просмотр остальных точек также не целесообразен;

3.Если точка неоптимальная, то нельзя ли определить вектор-столбец, подлежащий введению в базис, такой, что значение целевой функции будет обязательно больше предыдущего.

2.1.Основная теорема линейного программирования

Будем называть					(2.1.1)
∆j = (cBT Aj −c j )
оценкой вектора Aj .
Теорема: Пусть имеется базисное решение ЗЛП	x		B	= b	со значением
	xáàç =
		0

целевой функции f (xáàç ) = cBT xB = cBT b и для всех j найдены оценки ∆j = (cBT Aj −c j ) . Тогда:

1. Если имеется ∆j ≥ 0 для любых j, то базисное решение оптимально;

15

2. Если существует ∆k < 0 , то существует бесчисленное множество допус-

тимых решений x G , для которых f (x) > f (xáàç ) . При этом

2а. Если столбец Ak ≤ 0 , то задача неразрешима из-за неограниченности целевой функции;

2б. Если имеется aik > 0, то существует новое базисное решение, значение целевой функции на котором больше, чем на исходном , то есть

f (xáàçn ) > f (xáàç ) .

Замечание: Теорема справедлива, если базисное решение не вырождено, то есть b > 0.

На основе этой теоремы строится метод решения ЗЛП, называемый сим- плекс-методом, который фактически является методом перестроения базисного решения с учетом оценок небазисных столбцов.

2.2. Алгоритм симплекс метода

Пусть имеется базисное решение	x		B	= b	со значением целевой
	xáàç =
		0

функции f (x) = cTB xB .

Шаг 1: Вычислить оценки по формуле

∆j = ∑c j aij − c j при всех j.

i IB

Шаг 2: Если для j ∆ j ≥ 0 , то выписывается оптимальное решение задачи.

Конец. Иначе Шаг 3.

Шаг 3: Выбирается ∆k < 0.

Шаг 4: Просматривается столбец Ak , если Ak ≤ 0, то выписывается от-

вет:

«Задача не разрешима из-за неограниченности целевой функции». Конец.

Иначе Шаг 5.

Шаг 5: Алгоритм перестроения базисных решений ЗЛП. Шаг 6: Переход к Шагу 1.

Пример 2.1. Решить задачу

− x1 + x2 + x3				=1,
x1	− x2	+	x4	=1,
x1	+ x2	+	x5	= 2,

xi ≥ 0, i =1,5 ,

f (x) = 2x1 − x2 +3x3 − 2x4 + x5 → max .

16

Решение. Оформление задачи происходит аналогично предыдущему приме-

ру (табл. 2.1).
В последней строке, ранее не заполненной,													вписываются оценки и				f (xB ) ,
которые вычисляются по формуле f (x) = (cB , xB ) .															Таблица 2.1
B			cB				xB	2		-1		3		-2	1		θ
								A1		A2		A3		A4	A5
x3			3				1	-1		1		1		0	0		-
x4			-2				1	1		-1		0		1	0		1
x5			1				2	1		1		0		0	1		2
∆j							3	-6		7		0		0	0
x3			3				2	0		0		1		1	0
x1			2				1	1		-1		0		1	0
x5			1				1	0		2		0		-1	1
∆	j						9	0		1		0		6	0
Поскольку							на первой итерации				∆1	< 0 , в		базис вводится вектор A1.
1			2		,		то есть в качестве направляющего элемента выбирается a21 . Так
Θ = min		,		=1
1			1
как на второй						итерации		все	∆j ≥ 0 , то конец,				получена		оптимальная		точка

x* = (1,0,2,0,1) . Поскольку на небазисных векторах ∆j > 0 , то решение в задаче

единственно.

Пример 2.2. Решить задачу

				− x		+ x	2		− x		3		+ x		4			=1,
					1
					x1 − x2 +								+ x5					=1,
					x	−3x		2	+ x			3	+ + x				6	= 2,
					1
						xi ≥ 0, i =										,
														1,6
				f (x) = 2x1 − x2 + x3 +3x4 −2x5 + x6 → max .
	Решение. Оформление задачи происходит аналогично предыдущему приме-
ру (табл. 2.2).																					Таблица 2.2
B		cB	xB	2		-1							1					3	-2	1		θ
				A1		A2							A3					A4	A5	A6
x4		3	1	-1		1							-1					1	0	0		-
x5		-2	1	1		-1							0					0	1	0		1
x6		1	2	1		-3							1					0	0	1		2
	∆	j	3	-6		3							-3					0	0	0
x4		3	2	0		0							-1					1	1	0
x1		2	1	1		-1							0					0	1	0
x6		1	1	0		-2							1					0	-1	1
	∆	j	9	0		-3							-3					0	6	0

17

На второй итерации получаем, что оценка ∆2 < 0, но в столбце А2 нет по-

ложительных элементов.

Ответ: целевая функция неограниченна.

Лабораторнаяработа №3

Решить симплекс-методом ЗЛП из лабораторной работы № 2.

2.3. Симплекс-метод с искусственным базисом

Вернемся к алгоритму симплекс-метода и заметим, что его применение возможно только при наличии начального базисного решения. Однако его можно получить, только если матрица А имеет вид A = (E / Aˆ) . В этом случае

ЗЛП представляется в виде

xB + AˆxA = b, xB ≥ 0, xA ≥ 0,

f(x) = cBT xB + cTA xA → max

иимеется базисное решение с базисными компонентами xB = b .

Рассмотрим задачу.

Ax = b,
x ≥ 0,	(2.3.1)
f (x) = cT x → max,

где матрица А не имеет единичных столбцов или их число меньше числа строк матрицы.

В этом случае нет возможности найти начальное базисное решение, более того задача (2.3.1) может оказаться несовместной.

Поэтому задача решается в два этапа. На первом этапе отыскивается начальное базисное решение, а на втором – решается исходная задача с помощью алгоритма симплекс-метода.

Задача первого этапа:

Ax + Ez = b ,
x ≥ 0, z ≥ 0 ,	(2.3.2)

fˆ(x, z) = −∑zi → max.

Переменные zi называются искусственными переменными.

Утверждение 1: Задача (2.3.2) разрешима.

Утверждение 2: Если при решении задачи (2.3.2) получено оптимальное

решение x0 = (x0 , z0 )T и fˆ(x0 , z0 ) = 0 , то точка x0 = (x10 ,..., xn0 ) является допустимым решением задачи (2.3.1).

Утверждение 3: Если оптимальное значение целевой функции fˆ(x0 , z0 ) < 0, то допустимое множество задачи (2.3.1) пусто.

18

На основе утверждений 1-3 и строится алгоритм симплекс-метода с искусственным базисом.

Алгоритм симплекс-метода с искусственным базисом Шаг 0: Приведение к канонической форме.

Шаг 1: Запись всех исходных данных в таблицу.

Шаг 2: Просмотреть столбцы матрицы A и отыскать единичные столбцы с единицами в разных позициях. Соответствующие переменные занести в гра- фу-базис.

Шаг 3: Просматривается базисный столбец, если он заполнен, то переход к алгоритму симплекс-метода.

Конец. Иначе Этап 1.

Этап 1

Шаг 1: Свободные места в базисном столбце заполняются переменными zi с номерами соответствующими номерам строк.

Шаг 2: Целевые коэффициенты при переменных xi полагаются равными

нулю (ci = 0).

Целевые коэффициенты при zi полагают равными минус единице. Шаг 3: Переход к алгоритму симплекс-метода.

Шаг 4: Если fˆ(x)îïò < 0, то выписывается ответ: Задача несовместна.

Конец.

Иначе переход к Этапу 2.

Этап 2

Шаг 1: Для всех переменных xi целевые коэффициенты полагаются рав-

ными сi .

Шаг 2: Переход к алгоритму симплекс-метода. Конец.

Замечание 1: Единичные столбцы, соответствующие переменным zi , в

таблицу не заносятся.

Пример 2.3. Решить задачу:

− 2x1 + x2 + x4 − x5 = 3, 2x1 − x2 + x3 − x4 − 12 x5 =1,

− x1 + x2 − x3 + 23 x4 + x5 = 8, x1 ≥ 0 ,

f (x) = x1 − x2 + x3 −3x5 → max .

1.Занесём все данные задачи в табл. 2.3.

19

Таблица 2.3

B	cв	xв	1	-1	1	0	-3
			A1	A2	A3	A4	A5
		3	-2	1	0	1	-1
		1	2	-1	1	-1	-1⁄2
		8	-1	1	-1	2⁄3	1

2. Просматриваем табл. 2.3 и отыскиваем единичные столбцы для введения их в базис.

В таблице таких столбцов нет, поэтому в графу В заносят три искусственные переменные, а в графу cв - коэффициент (-1) (табл. 2.4).

Таблица 2.4

B	cв	xв	0	0	0	0	0	Ө
			A1	A2	A3	A4	A5
z1	-1	3	-2	1	0	1	-1
z2	-1	1	2	-1	1	-1	-1⁄2
z3	-1	8	-1	1	-1	2⁄3	1

3. Вычисляем значения целевой функции по формуле															f (x) = ∑ci xi . Вы-
числяем оценки по формуле ∆j = ∑ci Aij − c j									(табл. 2.5).			Таблица 2.5
	B	cв	xв	0	0				0		0		0		Ө
				A1	A2				A3		A4		A5
	z1	-1	3	-2	1				0		1		-1
	z2	-1	1	2	-1				1		-1		-1⁄2
	z3	-1	8	-1	1				-1		2⁄3		1
			-12	1	-1				-1		-2⁄3		1⁄2
4. Так как ∆4<0, то x4 можно ввести в базис.
Вычисляем θ по формуле θ = min						xi	.
					aik >0	aik

Минимальному значению θ будет соответствовать место направляющего элемента в столбце x4.

Полностью все Шаги перестроения базисного решения представлены в табл. 2.6.

								Таблица 2.6
B	cв	xв	0	0	0	0	0		Ө
			A1	A2	A3	A4	A5
z1	-1	3	-2	1	0	1	-1
z2	-1	1	2	-1	1	-1	-1⁄2
z3	-1	8	-1	1	-1	2⁄3	1
		-12	1	-1	-1	-2⁄3	1⁄2

20