Учебное пособие 1282

ЗАНЯТИЕ № 3

ИССЛЕДОВАНИЕ И РЕШЕНИЕ ОДНОРОДНЫХ СИСТЕМ

Литература: [1], c. 267-269; [4], c. 45-50; [7], c. 142-143; [15], с. 30-34, [16],c. 36-39.

Контрольные вопросы и задания

1.Какая система линейных уравнений называется однородной?

2.Может ли однородная система быть несовместной?

3.Каковы необходимые и достаточные условия наличия у однородной системы ненулевых решений (с доказательством )?

4.Что называется фундаментальной системой решений однородной системы?

5.Как найти общее решение неоднородной системы, используя фундаментальную систему решений соответствующей однородной?

Примеры решения задач Пример 1. Найти фундаментальную систему решений и

общее решение однородной системы линейных уравнений

x1 2x2 2x3 3x4 0
	6x1 3x2 3x3 x4 0
	7x1 x2 x3 2x4 0
3x 9x 9x 10x 0
	1	2	3	4
Решение. Приведем		матрицу системы к треугольному

виду

88

8

1		2		2	3				умножим первое уравнение
	6	3		3	1				на 6, 7, 3 и прибавим
	7	1		1	2						последовательно
	3	9		9	10					ко 2, 3, 4 уравнению
1		2		2	3					умножим второе			уравнение
	0	15		15	19							на 1
	0	15		15	19					и прибавим последовательно
	0	15		15	19							к 3, 4 уравнению
		1		2		2			3
			0	15		15				19		1 2 2	3
			0 0			0			0				.
												0 15 15 19
			0	0		0			0
Таким		образом			матрица коэффициентов								имеет ранг

r 2 . Записываем систему уравнений с новыми коэффициен-

тами
	x1 2x2 2x3 3x4	0	.
	15x2 15x3 19x4 0

Так как ранг системы r 2 n 4 - числа переменных, то система имеет бесконечное множество решений. В качестве

главных переменных можно выбрать								x1	и x2 , соответствую-
щие столбцам ненулевого минора							1	2	; в качестве свобод-
							0	15
ных переменных – x3						и x4 . Из второго уравнения системы по-
лучим x	x		19	x		. Подставляя это выражение в первое
2	3	15			4

уравнение, получим

98

9

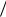
x 2x 2x 3x 2x															38			x 2x 3x								7		x .
1	2					3				4		3	15						4	3				4	15				4
Обозначаем свободные переменные через произвольные
постоянные x3 c1 , x4								c2			и записываем
		x						7		c	,						x c					19		c .
		1						15		2								2		1	15			2
Таким образом, общее решение системы имеет вид
			7		c							0 c		7			c										7
		15				2						1	15					2			0				15
		19											19								1				19
X	c1 15 c2											c1	15 c2							c1	1			c2	15				.
			c1									c1 0 c2													0
																					0
			c									0 c c													1
		2										1	2

Из общего решения находим фундаментальную систему решений:

		0				7
E		1 ,		E		19	.
1		1		2		0
		0				15

С использованием фундаментальной системы решений общее решение может быть записано в виде X c1E1 c2E2 ,

где c2 c2 15.
Пример		2.	Найти	общее решение неоднородной системы
4x1 x2 3x3 2x4 1
	8x1 5x2 6x3 3x4 2 , используя фундаментальную систе-
12x 7x 9x 5x 3
	1	2	3	4

му решений соответствующей однородной системы.

100 8

10

Решение. Замечаем, что частным решением данной неодно-

родной системы является Xчн 1, 2, 1, 2 .
Приведем матрицу системы к треугольному виду
4	1	3	2		4		1	3	2	4			1	3	2
	5	6	3			0	3	0			0	12		0	4
8									1
	7	9	5			0	4	0			0		12	0	3
12									1

				4		1 3 2						4		1 3	2
					0 12 0 4								0	3 0 1
																.
					0 0 0 1								0	0 0 1
			Таким образом, однородная система примет вид
						4x1 x2 3x3 2x4 0
												3x2 x4 0 .
														x4 0
			Решение	этой			системы				имеет			вид x4 0 ,			x2 0 ,
x		3	x . Обозначая			x		4c ,	получим общее решение одно-
1		4	3			3
							3c		3
родной системы				X	0			0 c		0	. Общее решение исходной
							4c			4
										0
								0

неоднородной системы будет иметь вид
				3			1				3c 1
					0			2			2
X X	0	X	чн	c								,
					4			1			4c 1
					0			2			2
т.е. x1 3c 1, x2 2 ,				x3 4c 1,					x4 2 .
				1
				118
				11

Задачи и упражнения для самостоятельного решения

Решить задачи: [7], 3.225-3.232; 3.236-3.239; [15] упр. с. 34-36.

Форма отчетности: устный опрос, контрольная работа.

ЗАНЯТИЕ № 4

СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ. ДВОЙНОЕ ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ

Литература: [1], c. 190-195; c. 25-31, [16],c. 50 -52.

Контрольные вопросы и задания

1. Дайте определение смешанного произведения векто-

ров.

2.Каковы свойства смешанного произведения векторов?

3.Каково необходимое и достаточное условие компланарности векторов?

4.Как выражаются векторное и смешанное произведения через координаты перемножаемых векторов (с доказательством)?

5.Каков геометрический смысл смешанного произведения векторов?

6.Дайте определение векторного произведения.

7.Как находится двойное векторное произведение?

Примеры решения задач

Пример 1. Даны вершины пирамиды: A 5,1, 4 , B 1, 2, 1 ,

C 3,3, 4 , D 2, 2, 2 . Найти длину высоты h , опущенной из вершины D на грань ABC .

Решение. Так как объем пирамиды есть V 13 Sh , то h 3SV ,

где S – площадь основания ABC .

122 8

12

Находим V							как						1					объема параллелепипеда, построенного на
							6
векторах AB , AC и AD . Определяем координаты этих векто-
ров:		4,1,3 ,																							2, 2, 0 ,																						3,1, 6												и вычисляем
	AB																		AC																									AD
объем пирамиды:
										1																														1			4					1	3					1
					V																																						2									|							24			4 .
														AB									AC							AD												|						2 0
							6																														6						3					1	6					6
Находим площадь основания ABC :
					1																					1							i						j				k					1
	S							AB AC																					|		4						1 3									|				6	i		6					j		6		k		3 3 .
				2																						2					2						2						0					2
																			3 4
Следовательно, h																															4						3	.
																		3 3																3
																																								a 2, 3,1 ,																	3,1, 2 и
Пример				2.				Даны														векторы																																		b
c 1, 2,3				. Вычислить																						a						b					c .

Решение. 1-й способ. Вычисляем сначала векторное произведение, стоящее в скобках:

						i					j				k
a			b		2					3					1				7			i	7			j	7			k	.
					3					1					2
Полученный результат умножаем векторно на c :
a		c						i					j					k
							7				7						7				7				14				7				.
	b																							i				j				k
							1			2					3

2-й способ. Воспользуемся формулой:

133 8

13

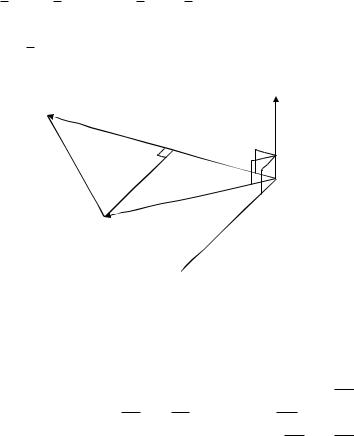
a b c b a c a b c b 2 6 3 a 3 2 6

b 5a 3 10, 1 15, 2 5 7,14, 7 .

E

B

D

C

A

F

Рис. 1

Задачи и упражнения для самостоятельного решения

Решить задачи: [6], 871, 873, 874 (1,2), 875, 876, 877, 878,

879, 881.

Указание к решению задачи № 881. Вектор CE

перпендикулярен векторам CB и CA , а вектор CF , парал-

лельный высоте AD , перпендикулярен векторам CE и CB (рис. 1).

Форма отчетности: устный опрос, типовой расчет, контрольная работа.

ЗАНЯТИЕ № 5

ЛИНЕЙНЫЕ ПРОСТРАНСТВА

Литература: [3], c. 80-114, 121-135; [8] c. 166-191; [15], с. 37-73, [16],c. 29-36.

144 8

14

Контрольные вопросы и задания

1.Дайте определение линейного пространства. Приведите примеры.

2.Что такое базис линейного пространства и его связь с размерностью линейного пространства?

3.Как определяется матрица перехода между старым и новым базисами?

4.Расскажите о линейном операторе.

5.Как выглядит матрица линейного преобразования в новом базисе?

6.Дайте определение собственных значений и собственных векторов.

Примеры решения задач

Пример 1. Является ли множество M m, n всех матриц размера

m n линейным пространством?

Решение. Проверим выполнение условий, пользуясь операциями над матрицами:

1) A B C , где A , B и C – матрицы размера m n . Поэтому первое условие выполняется.

2) A B , где A и B – матрицы размера m n , а – произвольное число. Поэтому второе условие выполняется.

3) Операции сложения матриц и умножения матрицы на число удовлетворяют следующим свойствам:

а) A B B A;

б) A B C A B C ;

в) A 0 A, где 0 – нулевая матрица;

г) A B 0 B A ;

д) 1 A A;

е) A A , где и – произвольные числа;

155 8

15

ж) A A A ; з) A B A B .

Таким образом, множество M m, n

всех матриц размера

m n является линейным пространством.

Пример

2.

Найти

координаты

геометрического

вектора

,

x i 2 j k в новом базисе B

где

e1, e2

, e3

e1 i j ,

i k .

e2 j k

, e3

,

в исход-

Решение. Выпишем координаты векторов e1

e2

и e3

ном базисе B

:

i

,

j

,

k

1

0

1

,

1 ,

0 .

E1 1

E2

E3

0

1

1

Составляем столбцы матрицы перехода

T

от старого

базиса к новому из записанных выше координат векторов и получаем

1		0	1
T	1	1	0	.
	0	1	1

Используя эту матрицу, получаем координаты вектора x в новом базисе:

					1	1	1		1			0
X T	1		1
		X			1	1	1		2			2 .
			2
					1	1 1			1
												1
Таким образом,
		x 2e2			e3 .

Пример 3.В L3 задан линейный оператор, матрица которого в базисе B e1, e2 , e3 равна

166 8

16

1		2	0
A	3	0	1 .
	2	5	3

Найти

матрицу

этого

оператора

в

базисе

B

e1, e1 e2

, e1 e2 e3 .

e1, e2

, e3

,

и

в исход-

Решение. Выпишем координаты векторов e1

e2

e3

ном базисе:

1

1

1

0

,

1

1 .

E1

E2

, E3

0

0

1

Составляем столбцы матрицы перехода T от старого базиса к новому из записанных выше координат векторов и получаем

1		1	1				1		1	0
						1
T	0	1	1	,	T			0 1		1 .
	0	0						0	0	1
			1

Находим матрицу оператора в новом базисе:

					1	1			0 1		2	0 1			1	1
		1
A	T		AT		0		1 1 3				0	1		0	1	1
					0						5	3		0	0
							0 1 2									1
	2 2				1 1				1	1	2 0				1
		1 5			4			0	1	1	1		4		8	.
		2 5			3			0	0						10
										1	2 7

Задачи и упражнения для самостоятельного решения

Решить задачи: [8], 1281, 1311, 1446, 1469; [15], упр. с. 51-55, с. 68-71, с. 83.

Форма отчетности: устный опрос, типовой расчет, контрольная работа.

177 8

17