Учебное пособие 1851

ортогональны ортам ei,i и а i , а также ei и аi .

При сборке звена i с уже собранной кинематической цепью орты

ei,i и а i и bi поворачиваются одинаково (поскольку связаны с звеном i)

и превращаются в орты ei , аi , bi . Поэтому можно построить три линейных преобразования на основе матрицы Пi .

o

Пi

ei,i

ˆ

= ei ,

o

Пi

ˆ

,

(4.4)

а i = аi

o

Пi

ˆ

,

bi = bi

где

m

o

0 m

m

ei,i ={e

} (m=1,2,3),

ˆ

i ,i

ei ={ei },

а i ={аi },

o

m

ˆ

0

аi

={аi },

m

o

0 m

ˆ

bi ={bi

}, bi

={bi

} – матрицы-столбцы.

Система (4.4) содержит 9 уравнений и 9 неизвестных эле-

ментов

ikl (k, l =1, 2, 3)

матрицы Пi .

Коэффициентами при

а i

неизвестных являются элементы матриц ei,i ,

и bi . Если

k

={

km

}, к-тая строка матрицы Пi и

i = {

1

2

3

}

T

=

i

i

i ,

i

,

i

{

i11 ,

i12 ,

i13 , … ,

i31 ,

i32 ,

i33 }Т – девятимерная матри-

kl

о Т

o Т

o Т

T

о 1

i = { eˆ i,i

, аˆ i

ˆ

ца-столбец неизвестных

i , а

, bi

}

= {ei,i

,

о 2

о 2

о 3

T

, … , bi ,

bi }

– девятимерная матрица-столбец, содержа-

eT

щая правые части системы (1), ˆ = {0, 0, 0} – нулевой трех-

0

мерный вектор, то система (4.1) может быть записана в виде

38

									Т
eˆ i,i	ˆ	ˆ	aˆ i	ˆ	ˆ	ˆ	ˆ	ˆ
	0	0		0	0	b i	0	0
ˆ	eˆ i ,i	ˆ	ˆ	aˆ i	ˆ	ˆ	ˆ	ˆ	i = .
0		0	0		0	0	b i	0
ˆ	ˆ	eˆ i ,i	ˆ	ˆ	aˆ i	ˆ	ˆ	ˆ
0	0		0	0		0	0	b i
Поскольку векторы ei,i и а i , bi						не коллинеарны, их ком-

поненты линейно независимы. Тогда строки блочной матрицы системы (4.5) также линейно независимы и определитель этой матрицы отличен от нуля. Поэтому система (4.4), а значит и система (4.5) имеет единственное решение, т.е. матрица Пi является единственной.

Для решения системы (4.4) необходимо иметь правые час-

	o	o	o	о
			ˆ
	ти eˆi	ˆ		Z .
		аi	и bi , заданные в неподвижной системе координат

Поскольку звено i-1 присоединено к звену i-2, то матрица Пi-1

		o		o			o	о
		ˆ	и	ˆ	1,i по формулам		ˆ	ˆ
известна и можно определить ei				ri			ei = ei,i =
о	o				o	o
		ˆ				ˆ
eˆi	ˆ		1,i ,		ˆ		- по ра-
	1,i = Пi-1 ei 1,i , r i 1,i	= Пi-1 r i			а матрицы аi и bi
нее полученным формулам (4.1) – (4.3).
	Систему (4.4) можно решить методом исключения Гаусса.
Поскольку орты осей системы Z i				при сборке поворачиваются

также, как и орт ei,i , можно записать систему

				о k		ˆ	k
				ˆ	= Пi			(к=1,2,3),
				qi		qi
	ˆ k	о mk	ˆ k	mk				k	k	k
	о	={ qi	}, qi	= { qi } – проекции ортов qi					и qi	осей Zi и
где qi
Z ik					о
	на оси систем координат Z и Z i .

Поскольку

39

qˆ i1 ={1,0,0}T,		qˆ i2 ={0,1,0}T,					qˆ i3 ={0,0,1}T,
о k			1к		2к		3к	T
qˆ i	={		i	,	i	, i		} ,

то есть элементы k-того столбца матрицы Пi равны проекциям

	Z ik системы
орта q ik оси			Z i	на оси неподвижной системы
о	после сборки.
координат Z
Для присоединения следующего звена необходимо опре-
				о
делить проекции ei,i 1		на	оси системы Z после сборки, т.е.
		o
найти матрицу столбец		ˆ	1 . Для этого можно воспользовать-
		ei
ся преобразованием:
		o	o
		ˆ	ˆ	1 =Пi ei,i 1 ,
		ei 1	= ei ,i

поскольку при сборке звена i векторы ei,i 1 и ei,i поворачиваются одинаково.

Далее описанный процесс можно повторить для звеньев i+1, i+2 и так далее вплоть до присоединения последнего звена механизма. Алгоритм сборки механизма очевиден. Процесс

сборки начинается с определения проекций орта e 0 ,0 базового

о

(нулевого) звена в системе Z , что соответствует установке ба-

зового звена в рабочем помещении. Можно считать, что Z 0

о

	совпадает с Z . В этом случае По= I.
	Поскольку матрицы Пi	известны,		известны и положения
		~			~	о
	всех звеньев ММ. Матрицы		преобразований			Z можно
		Кi			Zi
		~		о
	определить, зная положение		относительно Z . Но, посколь-
		Zi
			~	о	, К~i = Пi		1 .
	ку Пi матрица преобразования Z i Zi			и Z i = Z

40

~

~

~

ˆ

и

ˆ

1 проекции вектора

r

в системах Zi

и

~

Пусть r i

r

Zi 1 . Тогда

o

~

~

~

~

~

~

ˆ

ˆ

ˆ

=

ˆ

r =

Кi 1 r i 1

Кi r i

= Кi Кi ,i 1 ri 1 ,

~

1 матрица перехода

~

~

где

Кi ,i

Zi 1

Zi .

Отсюда следует

~

~

~

~

~

-1

~

1

Кi

1 = Кi

Кi ,i

1

и Кi ,i 1

=(

Кi

)

Кi 1 =Пi

Пi

1 .

(4.6)

~

~

~

Следовательно,

матрицы

Кi ,i 1

перехода

Zi 1

Zi для

конфигурации qˆ =0 определяется на основе матриц Пi

. В этом

и заключается основное назначение сборки механизма.

Для

конфигурации

ˆ

0

матрицы

перехода

Кi

q

~

~

Zi+1

Zi

1

Zi определяются по формулам:

~

1 Кq (I+1),

Кi = Кi ,i

(4.7)

где Кq (I+1) – матрица преобразования Zi+1

~

1 при qi+1

0,

Zi

компоненты которой зависят только от qi+1 .

Для поступательной кинематической пары с номером i+1

Кq (I+1) = I,

(4.8)

поскольку относительное вращение отсутствует и поворот на угол qi+1 не

~

возможен. Тогда Кi = Кi ,i 1 .

2.4.1.Второй способ сборки.

	~
	Пусть оси Z j ориентированы также как и оси системы координат
~	~	~	~
Zi	звена i, Ki, j -матрица [1] преобразования Z j		Zi . Сборку звена j со
		~
звеном i можно считать описанной, если		Ki, j	известна. Способ сборки,

~

описанный выше, основан, кроме прочего, на определении Ki, j из систе-

мы 9 линейных уравнений, и поэтому требует значительных вычислений и ориентирован на использование ЭВМ.

41

k

k

Пусть qˆ

j

- орт оси z j

системы Z j . Если ввести символ

Кронекера

lk

1, при k

l,

0, при k

l,

k

то

qˆ

j

примет вид

k

1k ,

2k ,

3k

T .

qˆ

j

Матрица -

столбец

~k

~

~k

равна, очевидно, столбцу мат-

qˆ

K

i, j

qˆ

j

i

~

~

рицы

Ki, j с номером k. Таким образом, столбец k матрицы

Ki, j равен

проекциям орта

k

на оси системы

~

Следовательно,

определение

q

j

Zi .

~

Ki, j

можно свести к определению проекций ортов осей системы Z j на

~

оси системы Zi

после поворота

Z j

так же, как и элемента звена j.

При решении многих задач теории манипуляторов используется формула Родриго (см. раздел 4), которая в матричной форме имеет вид

ˆ			ˆ		ˆ	, r
r		R(	, )rˆ		r
	p		e	, где		p ˆ - матрицы, определѐнные в одной систе-

ме координат, соответствующие повернутому и поворачиваемому векто-

рам; - угол поворота; eˆ - орт оси, вокруг которой происходит пово-

рот, определѐнный в той же системе координат;
R( ,eˆ ) I cos	( 1 cos )E D( eˆ ) sin	(4.9)

-матрица Родриго;

42

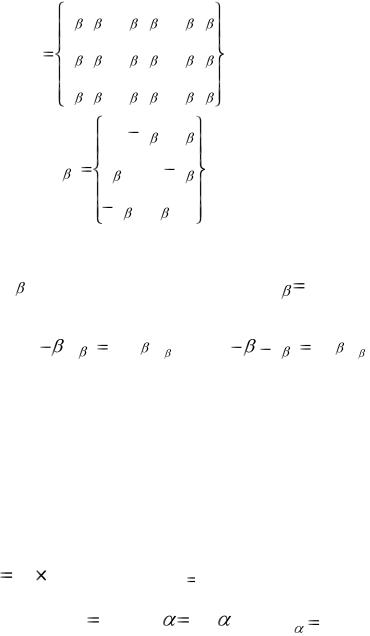
e1 e1	e1 e2	e1 e3
E e2 e1	e2 e2	e2 e3	,
e3 e1	e3 e2	e3 e3

0	e3	e2
D( eˆ ) e3	0	e1 .
e2	e1	0

d

Если

ˆ

- некоторый вектор, направленный вдоль оси вращения, то

ˆ

ˆ

d / d

e

орт

оси вращения определяется по формуле

e

ˆ

.

Легко проверить следующие свойства матрицы Родриго

R(

,ˆ

) RT ( ,

eˆ

) ,

R(

,

ˆ

) R( ,

eˆ

).

e

e

Пусть e j

и ei - орты собираемых элементов звеньев i и j. Для оп-

ределения угла поворота звена j нужно иметь проекции ei и

e j

на оси

какой либо системы координат. Анализ объѐма вычислений, необходимых

для описания сборки звеньев i и j, показывает, что наиболее удобно распо-
	~
ложить Z j	так же, как и систему Zi .

	ˆ	e	j
Пусть известны	ei	и ˆ		. Тогда, используя формулу

ci

e

j

e

i

c

i

ˆ

e

i

ˆ

, или формулу ˆ

e j

) ˆ

, получаем матрицу

ci

.

D (

,

,

ci e jei sin

sin

/ c

Очевидно, что

, а орт e

c

указы-

i

i

вает ориентацию оси вращения звена j при сборке его со звеном i. 43

Очевидно, что

		3	2 1 / 2 .
sin	Ci		( cik )
	k		1

		ei
e j
Если	и			совпадают или противоположны по направлению,
модуль вектора ci			равен нулю, поскольку при этом =0 или = . В
этом случае для определения						можно использовать скалярное произве-
					T
		j		ei	ˆ	e
дение векторов e			и		e j	ˆ	i	cos .
Если		0 ,	то векторы e j					и ei	совпадают и поворот на угол
не нужен.	Если				, то поворот можно произвести относительно

любого орта. Для определенности поворот будем производить с использо-

ванием матрицы Родриго вокруг орта, направленного так же, как и нор-

мальная к орту e j

составляющая вектор - радиуса

r i , j .

При повороте звена j на угол

рассмотренным способом всѐ зве-

но j, а значит и система Z j

, поворачивается на угол

. Орты Z j

в

повѐрнутом положении образуют систему координат

Z j

звена j, соб-

ранного со звеном i при некотором значении

qi

q

0 . Для определе-

ния угла поворота q звена j относительно звена i используются векторы

N

r iN,i

( r i,i

( r i,i ei )ei

,

,

r j,i

r j,i

( r j,i

ei

)ei ,

N

N

нормальные e i . Угол, отсчитанный от r i,i

до

r

j,i

против хода

часовой стрелки, если смотреть противоположно e i , равен q.

Пусть

44

	N	N	,		N	N	,
a	ri,i	/ ri,i		b	rj,i	/ rj,i

N

N

орты, соответствующие векторам

r i,i

, r j,i

и d

a b .

d

a, b

Для определения d нужны проекции векторов

и

на

~

оси какой либо системы координат, например Z j

. Тогда

ˆ

D(

ˆ

)ˆ

,

3

21 2

di

bi

k

ai

d (

)

( d i

k

1

Очевидно, что d

a b sinqi sinqi .

При определении q следует помнить, что функция Arcsin имеет глав-

ное значение в первой и второй четвертях, а при q=0 или q= модуль

вектора	d	равен нулю, и угол q можно определить только с точностью до

. Поэтому для определения угла q проще использовать скалярное произ-
			cos q	aˆ i	bi
ведение векторов a	и b	, поскольку		T	ˆ	.

При определении угла с помощью обратной тригонометрической функции следует помнить, что электронные вычислительные устройства возвращают только главное значение этой функции. Поэтому угол нужно определять с учетом расположения друг относительно друга ортов, образующих этот угол. Для этого удобно использовать изображения этих ортов в системе координат.

Повернув оси системы Z j на угол -q, вокруг орта e j с помо-

~

щью матрицы Родриго, получаем систему Z j . При q=0 поворот не нужен,

так как звено j уже имеет нужную ориентацию.

~ ~

Таким образом, для превращения системы Z j в Zi , нужно сначала

~

,

повернуть Z j на угол -q, а затем на угол . Подобным поворотам соот-

45

~

ветствует матрица Ki, j . Еѐ компоненты получаются двукратным использованием формулы Родриго.

~

,eˆ

) - матрица преобразования Z j

Легко видеть, что R(

Z j

~

q,eˆ

)

Z j . Тогда преобра-

Z j , а R(

j

- матрица преобразования Z j

~

~

Z j

зование Z j

Z j

Zi

определяется матрицей

~

R(

,eˆ

)R(

q,eˆ

) .

K

i, j

j

~

Следует

помнить,

что

подобным способом

определяется

матрица

Ki, j

только для вращательной пары, соединяющей звенья i и j.

Для поступательной пары поворот на угол q не возможен. При относи-

тельном движении звеньев в подобной паре ориентация звена j относитель-

~

~

Z j

но звена i не изменяется. Поэтому преобразование Z j

Z j

Zi

вполне определено матрицей

~

R(

,eˆ

) .

K

i, j

~

~

~

0 .

Матрица Ki, j определяет преобразование Z j

Zi при q

i

Пусть K i, j - матрица преобразования Z j

~

~

. Тогда

Z j

Zi

Ki, j

~

Ki, j Kqi ,

где K qi - матрица поворота системы Z j

на угол qi

относительно

e i .

Если кинематическая пара i поступательная, то K qi

I .

Поскольку изменение

обобщѐнных

координат

ql

для

l

i

не

влияет на взаимное положение звеньев i и j, матрица

Ki , j преобразует

Z j

Zi . Таким образом,

сборка механизма позволяет определить мат-

46

рицы преобразований проекций векторов на оси систем координат звеньев, входящих в кинематические пары.

47