Второй семестр (вечерка) / Практика / 6. Задания и пример выполнения 2.2 (самое полное)

7

ПРИМЕР ВЫПОЛНЕНИЯ ТР-2.2.

Часть I «ФУНКЦИЯ : непрерывность, точки разрыва, корни, интервалы знакопостоянства, асимптоты».

Задание. 1.1 Указать область определения и “особые» свойства функции: чётность/нечётность, периодичность, симметрия графика. 1.2 Указать интервалы непрерывности и точки разрыва функции. (1.3) Найти корни f(x)=0 и интервалы знакопостоянства f(x)>0, f(x)<0 функции. 1.4 Найти прямолинейные асимптоты графика функции.

1.1 Область определения, особые свойства функции.

; График y=f(x) симметричен относительно прямой х_сим=-1, поэтому исследовать функцию можно лишь на интервале (-1;+∞).

1.2 Непрерывность, точки разрыва функции.

Как сумма элементарных функций функция f непрерывна на множестве . Точка является точкой разрыва 2 рода, так как односторонние пределы

1.3 Корни и интервалы знакопостоянства функции.

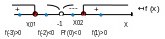
1.4 Асимптоты функции.

ХАС = -1 вертикальная асимптота при х→-1-0 и при при х→-1+0 ⇒ Рис.1:

Прямолинейные асимптоты на «+∞»/ на «-∞»:

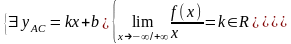
 Прямолинейных асимптот на «+∞»/ на «-∞» функция не имеет, так как

Рис.1

Часть II: Дифференцируемая функция: интервалы монотонности, локальные экстремумы.

Задание. 2.1 Определить производную функцию , найти её корни и интервалы знакопостоянства.

2.2 Указать интервалы монотонности функции f.

2.3 Найти критические точки и локальные экстремумы функции f.

==========================================================================

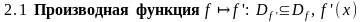
f '(x) = 2((x+1)⁴+9) : ((x+1)³ ; D_f’=(- ∞;-1)U(-1; +∞)

_{f’непрерывна, точка разрыва хр=-1}

_{f’(x)=0 ⇔ ᴓ f’ корней не имеет; f’(x<-1) < 0 ∧ f’(x > -1) > 0}

2.2 Интервалы монотонности функции f.

«Функция f возрастает на (a;b), если f’ > 0, и убывает на (a;b), если f’ < 0»

_{ f’(x < -1) < 0 ⇒ ↓f(x<-1) – f монотонно убывает на (- ∞;- 1) f’(x >-1) > 0  ↑f(x > -1) – f монотонно возрастает на (- 1; +∞)}

_{2.3 Локальные экстремумы (ЛЭ) функции} f_.

_{Необходимый признак ЛЭ: «Непрерывная функция f имеет локальный экстремум только в «критической точке хК функции»: Достаточный признак ЛЭ: «Функция f имеет в точке хК локальный экстремум, если (при «переходе через хК » производная «меняет знак!) хК = xmin  хК = xmax }

_{----------------------------------------------------------------------------------------------------------------------------}

_{ Функция f критических точек не имеет.} Следовательно, _{локальных экстремумов функция f не имеет.}

_{Результаты. Функция f монотонно убывает на (- ∞;- 1) и монотонно возрастает на (- 1; +∞)}

_{Локальных экстремумов функция не имеет.}

Рис.2

_{=============================================================================}

Часть III: Дважды дифференцируемая функция: интервалы выпуклости/ вогнутости и точки перегиба функции. Задание. 3.1 Определить вторую производную функцию f”, указать интервалы её непрерывности, найти корни и интервалы знакопостоянства. 3.2 Указать интервалы выпуклости/ вогнутости и точки перегиба функции f.

3.1 Вторая производная функция

f ”(x) непрерывна на .

f”'(x) > 0 ⇔ ; f”'(x) < 0 ⇔

3.2 Интервалы выпуклости/ вогнутости и точки перегиба функции f.

«Дважды дифференцируемая функция f выпукла/вогнута на (a;b) , если f’’< 0 / f’ > 0»

• Интервалы выпуклости функции f:

• Интервалы вогнутости функции f:

_{«Точка xП является точкой перегиба дважды дифференцируемой функции f , если (при «переходе через xП » производная f’’«меняет знак!)}

 Функция f имеет две точки перегиба:

Рис.Точки перегиба

Часть IVI: Таблица результатов исследования и схематический график функции.

РЕЗУЛЬТАТЫ. Свойства функции: f: D_f=(-∞;-1)U(-1;+∞) → E_f, Корни, точки разрыва, интервалы знакопостоянства, асимптоты. Интервалы монотонности, локальные экстремумы. Точки перегиба, интервалы выпуклости и вогнутости.

X	(-∞;xper)	xper ≈ - 3.28	(xper;x01)		X01≈ - 2.73	(X01;-1)	XР= -1
f(x)	> 0 ∞↤f↓	3.46	> 0 f↓		0	< 0 f↓	f(х∓0)→- ∞
f’(x) αkac0	< 0	-6.08 -810	< 0		-6.93 -820	< 0	НЕ СУЩ. +/-∞
f”(x)	> 0 ВОГН.	0	< 0 ВЫП.		-4	< 0 ВЫП.	НЕ СУЩ. - ∞
Знакопостоянство	f(x)>0				корень	f(x)< 0
Монотонность	<--------------------------------f↓ убывает -------------------
Вып./вогнутость	вогнутая	Т. перегиба		--------выпуклая----------------			ХАС=хсим

X	XР= -1	(-1;x02)	X02≈ 0.73	(x02;XП2 )	XП2≈ 1.28	(XП2;+∞)
f(x)	f(х∓0)→- ∞	< 0 f↑	0 f↑	> 0 f↑	3.464 f↑	> 0 f↑→+∞
f’(x) αkac0	НЕ СУЩ. +/-∞	> 0	6.93 820	> 0	6.08 810	> 0
f”(x)	НЕ СУЩ. - ∞	< 0 ВЫП.	-4	< 0 ВЫП.	0	> 0 ВОГН.
Знакопостоянство		f(x)< 0	корень	f(x)>0
Монотонность		<---------------------------------f↑ возрастает ----------------------
Вып./вогнутость	ХАС=хсим	--------выпуклая-----------------			Т. перегиба	вогнутая

Схематический график функции.