4

ГЛАВА «ЧИСЛОВЫЕ РЯДЫ»

§1 Числовой ряд: основные понятия и примеры.

Пусть задана числовая последовательность Определим другую числовую последовательность

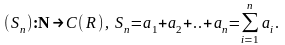
Определение 1. Пара числовых последовательностей

называется числовым рядом, при этом последовательность (1) называется последовательностью членов ряда (a_n – n-ый член ряда), а (2) - последовательностью

частичных сумм ряда ( S_n- n-ая частичная сумма ряда).

Следствия. 1) Числовые последовательности (1) и (2) взаимно однозначны:

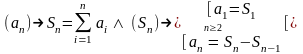
2) В дальнейшем выражение будем называть числовым рядом.



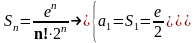
------------------------------------------ Определение 2. Если существует конечный предел последовательности частичных сумм ряда , говорят, что «ряд сходится», этот предел называют «суммой ряда» и пишут .

В противном случае 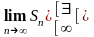говорят, что «ряд расходится».

Примеры.

1. Геометрическая прогрессия со знаменателем “q∊R\{0,1}”

Известно:



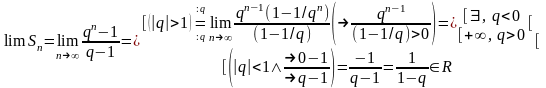
ряд сходится при |q|<1 к сумме ряда S= 1/(1-q) (сумма бесконечно убывающей геометрической прогрессии) и расходится, если |q| > 1.

(1)

(2)

(3)

§2 Свойства сходящегося числового ряда.

Из определения сходимости числового ряда и свойств пределов следуют СВОЙСТВА ЧИСЛОВЫХ РЯДОВ:

1. НЕОБХОДИМЫЙ (но не достаточный ! ) признак СХОДИМОСТИ числового ряд.

«Если числовой ряд сходится, предел его общего члена равен нулю.»

ДОСТАТОЧНЫЙ признак РАСХОДИМОСТИ числового ряда. «Если предел общего члена ряда не равен нулю, ряд расходится

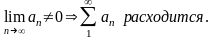
2. «Арифметические свойства».

5. Запишем числовой ряд в виде

Числовой ряд 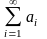и «остаток ряда» сходятся и расходятся одновременно.

Для сходящегося ряда верно числовое равенство

,

при этом . Следовательно, частичная сумма сходящегося ряда даёт «приближенное значение» («оценку») суммы ряда

АЛГОРИТМ исследования числового ряда:

[1] Исследование(установление) сходимости/ расходимости ряда:

Задача [1] решается либо «по определению» ,

либо с помощью «признаков сходимости/расходимости» рядов – теорем, устанавливающих связь между сходимостью/расходимостью ряда и свойствами членов ряда. Например, «достаточный признак расходимости» (2.) числового ряда: .

[2] Для получения «оценки» суммы сходящегося числового ряда используется числовое равенство S=S_K+R_K:

Определение. Пусть ряд сходится и получена оценка «сверху» модуля суммы его остатка R_K

Интервал 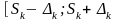], «накрывающий» сумму ряда S, называют “оценкой суммы ряда с погрешностью 2Δ_К» .

S_k-∆_k s_K S_k +∆_k

-----------(--------●----●----)---------------------> s

Очень важное Замечание Все промежуточные вычисления S_K, Δ_K, S_K ± Δ_K выполняются в «полной разрядной сетке», при этом Левый конец интервала округляется «по недостатку» 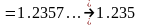, а правый – «по избытку»: →S∊[1.235;1.245]- оценка суммы ряда с погрешностью 0.010.