Четвертый семестр (вечерка) / ИДЗ / 5. Уравнение Шредингера / ИДЗ по теме уравнение Шредингера Попов А. П. гр. 8802

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра Физики

Индивидуальное домашнее задание

по дисциплине «Физика»

Тема: Уравнение Шредингера

Студент гр. 8802 __________________ Попов А. П.

Преподаватель __________________ Чурганова С. С.

Санкт-Петербург

2020

1. Написать уравнение Шрёдингира для стационарных состояний

Ответ.

- ψ + Uψ = Eψ

Или в кратком варианте:

ψ + (E-U)ψ = 0

, где m – масса частицы. – смотри 7 вопрос. U – Функция координат и времени, градиент которой, взятый с обратным знаком, определяет силу, действующую на частицу. В случае, когда функция U не зависит явно от времени, она имеет смысл потенциальной энергии частицы. E – полная энергия частицы, которая в случае стационарного поля остается постоянной. Ψ – пси функция, вид которой получается из решения уравнения Шредингера. – постоянная Диарака.

2. Написать выражение для волновой функции, описывающей одномерное движение свободной частицы

Ответ.

Частица движется в отсутствие внешних полей, т.е. U = 0, E = E­­­­­_k (полная энергия частицы равна кинетической энергии).

3. Написать одномерное временное уравнение Шредингера

Ответ.

, где

4. Временная часть уравнения Шредингера имеет вид . Найти решение уравнения

Ответ.

Найдем общий вид волновой функции, соответствующей стационарному состоянию. (напряженность =E) в уравнении не зависит явно от времени, тогда волновую функцию Ψ (x,y,z,t)  следует искать в виде произведения двух функций Ψ (x,y,z,t)  = ψ (x,y,z) φ(t), одна из которых зависит только координат, другая – от времени.

Подставляя волновую функцию в уравнение, и разделив затем обе части уравнения на  ψ (x,y,z) φ(t), получаем

= ψ

Для функции ψ (x,y,z)

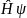=E .

ψ+Uψ=Eψ;

ψ+ (E - U) ψ = 0.

5. Написать уравнение Шредингера для стационарных состояний (случай трёх измерений)

Ответ.

+ + + (E - U) ψ = 0.

6. Написать уравнение Шредингера для стационарных состояний в операторной форме (случай трёх измерений)

Ответ.

ψ + (E-U) = 0

7. Как называется и что обозначает значок Δ в уравнении Шредингера в операторной форме. Ответ.

Значок Δ или же – это оператор Лапласа, результат действия которого на некоторую функцию представляет собой сумму вторых частных производных по координатам (градиент второго порядка).

+ + =

8. Написать временное уравнение Шредингера (случай трех измерений)

Ответ.

+ U (x,y,z,t) * = iħ

9. Написать временное уравнение Шредингера в операторной форме

Ответ.

( + + )+ U (x,y,z,t) * = iħ

10. Написать выражение для волновой функции, описывающей движение свободной частицы  (трехмерный случай)

Ответ.

|ψ( ,t)|²dv ≡ |ψ(x, y, z, t)|²dxdydz это вероятность найти частицу в области пространства объемом dv = dxdydz вокруг точки x, y, z.

11. Написать уравнение Шрёдингера для электрона, находящегося в водородоподобном атоме

Ответ.

Потенциальная энергия электрона в атоме где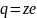 -заряд ядра => или

12. Написать уравнение Шрёдингера для свободного электрона, движущегося в положительном направлении оси Х со скоростью V. Найти решение этого уравнения.

Ответ.

У свободной частицы потенциальная энергия равна нулю, поэтому

Eψ = - .

Умножим на и пусть k² = , тогда

+ k²ψ = 0 – искомое уравнение.

Решение ищем в виде = Ae^λx, где A – амплитуда, λ – длина волны. Такое параметрическое уравнение имеет вид λ² + k² = 0, тогда

Ψ = A₁e^ikx + A₂ e^-ikx.

С учетом зависимости ориентации от времени = A₁ e^i(kx-ωt) + A₂ e^-i(kx-ωt).

Первое слагаемое соответствует волне, движущейся в положительном направлении оси O_x, второе – в отрицательном. Полагая A₂ ⁼ 0, получаем

Ψ = A₁e^ikx

13. Написать выражение для собственного значения энергии частицы, находящейся на n-м энергетическом уровне в бесконечно глубокой одномерной потенциальной яме.

Ответ.

Такая яма описывается функцией

, где n – квантовое число.

14. Написать выражение, определяющие вероятность обнаружения частицы в интервале от X до X+dx (в одномерном случае)

Ответ.

dω = |ψ|²dx = | |² dx

15. Написать выражение, определяющие вероятность обнаружения частицы в интервале от до (в одномерном случае)

Ответ.

Согласно вероятностному смыслу волновой функции, вероятность обнаружения частицы в интервале x₁ < x < x₂ определяется выражением

p = dx

16. Почему при физической интерпретации волновой функции говорят не о самой функции, а о квадрате её модуля

Ответ.

Квадрат модуля волновой функции имеет определённый физический смысл. Аналогично тому, как в волновой оптике мерой интенсивности волны, является квадрат амплитуды, так является мерой интенсивности электронной волны, пропорциональной концентрации частиц.

17. Может ли быть больше единицы? Ответ обосновать.

Ответ.

Нет. Функция – это характеризующая вероятность. В курсе математической статистики разъясняется, что вероятность может принимать значения от 0 до 1.

18. Может ли быть больше единицы? Ответ обосновать.

Ответ.

Нет. Это тоже характеристическая вероятность.

19. Чем обусловлено требование конечности Ψ-функции?

Необходимостью четкой характеристики состояния микрочастицы и свойствами характеристической вероятности. Функция Ψ, характеризующая вероятность обнаружения микрочастицы в элементе объема, должна быть:

конечной (вероятность не может быть больше единицы);

однозначной (вероятность не может быть неоднозначной величиной);

непрерывной (вероятность не может меняться скачком).

20. Уравнение Шредингера для стационарных состояний имеет вид 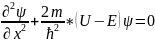. Исходя из этого уравнения, обосновать требования, предъявляемые волновой функции - ее непрерывность и непрерывность первой производной от .

Ответ.

Значение положительной энергии и полной энергии (Е), как и сама => 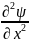должна быть ограничена. А это возможно, если непрерывна , но что бы существовала во всей интересующей нас области, 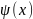должна быть непрерывна.

Условие непрерывности волновой функции. В любой момент времени волновая функция должна быть непрерывной функцией пространственных координат. Кроме того, непрерывными должны быть также частные производные волновой функции , , . Эти частные производные функций лишь в редких случаях задач с идеализированными силовыми полями могут терпеть разрыв в тех точках пространства, где потенциальная энергия, описывающая силовое поле, в котором движется частица, испытывает разрыв второго рода.