Методы математической физки Меркулов

равновесия, придав ее точкам на отрезке [ l; l] скорость v в начальный момент времени.

Функция u(x; t), описывающая колебания рассматриваемой струны,

является решением задачи:
	@2u			@2u
			= a2		;	1 < x < +1; t > 0;
	@t2			@x2
						u(x; 0) = 0;	2 [[ l; l]]:
			@t	= (x) = (0; x
		@u(x; 0)				v; x	l; l ;
							62

Если струна совершает колебания в результате того, что ее точки в начальный момент времени получили некоторые начальные скорости (например, по струне ударили), тогда говорят, что по струне распространяются волны импульса. Найдем эти волны. Применяя формулу Даламбера, получим:

u(x; t) = 2a

x+at

( )d = 2 ( (x + at) (x at)) ;

Z

1

1

x at

8

vl

;

x < l;

x

>

>

>

>

>

>

>

1

Z

>

vx

где (x) =

( )d

=

;

l x l;

a

a

0

<

>vl

x > l:

>

;

>

> a

>

vl

>

>

>

h =

тогда

Обозначим

,

:

a

8hx;

(x) =

l x

l;

h;

x < l;

>

l

<

>h;

x > l:

Полученное решение u(x; t) можно:

рассматривать как полусумму двух волн

отклонения (x + at) и (x at), распространяющихся влево и вправо. Найдем отклонение точек струны в моменты времени t0, t1, t2, t3:

1

u(x; t0) = u(x; 0) = 2 ( (x) + ( (x))) = 0;

90

u(x; t1) = u	x; 2a		=	2	x +	2		+ x	2		;
		l		1		l			l

u(x; t2) = u x;	l		=	1			( (x + l) + ( (x l))) ;
	a			2

u(x; t3) = u x;	2l	=	1		( (x + 2l) + ( (x 2l))) :
	a		2

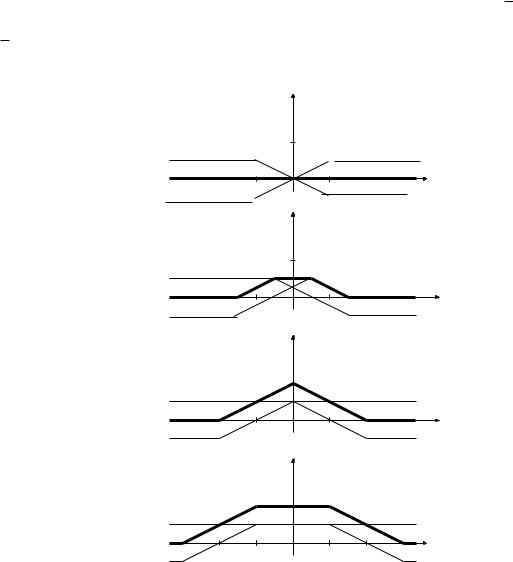
Изобразим на рис. 3.6 последовательные положения волн 12 (x + at) и

1 (x at), а также их сумму – функцию u(x; t) в моменты времени t0, t1,2t2, t3.

		u
			h		0.5 Ψ( x )
					u ( x , t 0 )
	−l	o		l		x
		0		l
		u			−0.5 Ψ ( x )
			h	0.5 Ψ( x + 0.5 l )
					u ( x , t1 )
	−l	0		l		x
		u		−0.5 Ψ ( x − 0.5 l )
			h		0.5 Ψ( x	+ l )
					u ( x , t2 )
	−l	0		l		x
		u			−0.5 Ψ ( x − l )
			h
					u ( x , t3 )
−2 l	−l	0		l	2 l	x
0.5 Ψ( x + 2 l )					−0.5 Ψ ( x	− 2 l )

Рис. 3.6

Характер колебаний струны, возникающих в результате импульсного воздействия на струну в начальный момент времени, существенно отличается от распространения волн отклонения. Согласно полученному решению после удара по струне она начинает подниматься в центральной части. При

91

t = 2la она имеет форму равнобедренной трапеции высотой h2 = 2vla. Затем,

при t = 2l струна принимает форму треугольника высотой h = vla . После

этого наибольшее отклонение точек струны не меняется и остается равным h, струна приобретает форму трапеции с высотой h. Далее основания этой трапеции начинают увеличиваться. Струна “поднимается”.

3.4. Колебания полубесконечной струны

Рассмотрим теперь задачу о поперечных колебаниях полуограниченной струны x 0 с жестко закрепленным концом. В этом случае к уравнению колебаний

@2u		= a2		@2u	;		0 < x; t > 0;	(3.5)
	@t2			@x2
и начальным условиям
		u(x; 0) = '(x);
			@u(x; 0)					(3.6)
							= (x)
				@t
следует добавить краевое условие
				u(0; t) = 0:				(3.7)

При этом '(0) = 0, иначе краевое и начальные условия будут не согласованы.

Для того чтобы решить поставленную задачу, рассмотрим сначала вспомогательную задачу. Вместо полуограниченной будем рассматривать неограниченную струну, при этом функции '(x) и (x) продолжим на отрицательную часть оси нечетным образом. Тогда для неограниченной струны получим следующую задачу:

@2u

@2u

= a2

;

1 < x < +1; t > 0;

@t2

@x2

u(x; 0) = (x);

@u(x; 0)

= (x);

@t

где

(x) =

'(x);

x 0; (x) =

(x);

x);

x 0;

(

'( x);

x < 0;

(

(

x < 0:

При этом ( x) = (x);

( x) = (x):

92

Решение находим по формуле Даламбера:

u(x; t) = (					) 2	+ 2a		x+at
		x		at				Z	( )d :
					+ (x + at)		1

x at

Покажем, что при t 0 и x 0 полученная функция u(x; t) является также решением задачи для полуограниченной струны. Действительно, u(x; t) удовлетворяет уравнению (3.5). Покажем, что для нее выполняются краевое и начальные условия (3.6), (3.7).

При x = 0 имеем

				at
u(0; t) =	( at) + (at)	+	1	Z	( )d = 0;
	2		2a
				at

так как ( at) = (at) и интеграл от нечетной функции (x) по симметричному промежутку также равен нулю.

При t = 0 и x > 0

u(x; 0) = (x) = '(x);

@u(x; 0) = (x) = (x): @t

Таким образом, если решение задачи о колебаниях неограниченной струны, полученной при нечетном продолжении функций '(x) и (x) через начало координат, рассматривать только при x 0, то получится решение задачи о колебаниях полуограниченной струны с жестко закрепленным концом.

Пример 3.4. Изобразить форму полубесконечной струны вблизи закрепленного конца в моменты времени t1 = 2al, t2 = 25al , t3 = 3al, t4 = 27al ,

t5 = 4al, если в начальный момент времени струну с закрепленным концом

x = 0 оттянули и на участке [2l; 4l] придали ей форму параболы с максимальным отклонением l2, т. е. начальное положение точек струны опи-

сывается функцией	'(x) =	(x 2l)(x 4l); x 2 [2l; 4l];		и начальная
		(0;	x [2l; 4l];
			62
скорость точек струны равна нулю:			(x) = 0.

Покажем как происходит процесс отражения волн от закрепленного конца, решая поставленную задачу о распространении волн отклонения. Функция u(x; t), описывающая колебания полубесконечной струны, явля-

93

ется решением задачи (3.5)–(3.7). Учитывая начальные условия, получим

u(x; t) = (x at) + (x + at);

2

где (x) получена из функции '(x) нечетным продолжением через начало координат (рис. 3.7).

u

ϕ( x )

−4 l −3 l −2 l −l 0

l

2 l 3l

4l

x

Φ ( x )

Рис. 3.7

Функцию u(x; t) будем рассматривать только при x 0, учитывая, что она представляет собой сумму двух волн отклонения, определенных на всей оси. Одна волна распространяется влево, другая – вправо. В указанные

моменты времени вершина параболы волны 12 (x at) будет находиться

в точках l, 2l , 0, 2l , l, а волны 12 (x + at) – в точках l, 2l , 0, 2l , l соответственно. Волны накладываются одна на другую, что соответствует

процессу колебаний (рис. 3.8).

На рисунках показан процесс отражения волны от закрепленного конца. Сначала волна деформируется, затем выпрямляется, а после этого переворачивается.

3.5. Метод Фурье

Рассмотрим теперь задачу о свободных поперечных колебаниях струны длины l, закрепленной на концах x = 0 и x = l. Эта задача сводится к решению уравнения

@2u			@2u						(3.8)
		= a2			; 0 < x < l;			t > 0;
	2		@x	2
	@t
с начальными условиями
	u(x; 0) = '(x);					@u	=	(x)	(3.9)
						@t

94

U

T = T1

−4 L −3 L −2 L −L 0 L 2 L 3 L 4 L

U

T = T2

−4 L −3 L −2 L −L 0 L 2 L 3 L 4 L

U

T = T3

−4 L −3 L −2 L −L 0

L 2 L 3 L 4 L

U

T = T4

−4 L −3 L −2 L −L 0 L 2 L 3 L 4 L

U

T = T5

−4 L −3 L −2 L −L 0 L 2 L 3 L 4 L

X

X

X

X

X

Рис. 3.8

и краевыми условиями

u(0; t) = 0; u(l; t) = 0;

(3.10)

где '(x) и (x) – заданные функции.

Метод Фурье применяется для решения поставленной задачи так же,

95

как и для уравнения теплопроводности. Данная задача уже является задачей с однородными краевыми условиями. (Если бы краевые условия были неоднородными, задачу следовало бы сначала свести к задаче с однородными условиями.)

1. Для линейного дифференциального оператора Lx(y) = y00(x) решим задачу Штурма–Лиувилля

y00(x) = y(x) ; 0 < x < l;

y(0) = 0; y(l) = 0:

Эта задача уже рассматривалась в 1.3. Собственные числа оператора

k = k2	=	k		2
				; k = 1; 2; ::: :
		l

Каждому собственному числу k соответствует собственная функция

yk(x) = sin	l		:
	kx

Система fyk(x)g+k=11 является полной ортогональной в пространстве L2[0; l] системой функций и может быть использована для разложения в ряд Фурье функций из этого пространства.

2. Функцию u(x; t) будем искать в виде ряда Фурье по ортогональной системе функций fyk(x)g+k=11

+1
Xk	(3.11)
u(x; t) = ck(t)yk(x):
=1

Краевые условия (3.10) для функции u(x; t) будут в этом случае автоматически выполняться. Подставим этот ряд в уравнение (3.8) и начальные условия (3.9). Предварительно разложим функции '(x) и (x) в ряды Фурье по той же системе функций:

					+1
					Xk
			'(x) =		'kyk(x);
					=1
					+1
					Xk
			(x) =		kyk(x);
					=1
где 'k =	('(x); yk(x))	,	k =	( (x); yk(x))		.
	kyk(x)k2			kyk(x)k2
Сначала подставим ряд (3.11)					в дифференциальное уравнение (3.8)
	+1				+1

XX

ck00(t)yk(x) = a2	ck(t)yk00(x):
k=1	k=1

96

Используя равенство yk00(x) = kyk(x) ( k = 2k), получим

+1

+1

XX

	ck00(t)yk(x) = a2 k2ck(t)yk(x):
k=1	k=1

Поскольку разложение в ряд Фурье обладает свойством единственности, приравняем коэффициенты полученных рядов Фурье:

c00k(t) = a2 2kck(t); k = 1; 2; ::: :

Функции ck(t) являются решениями линейных дифференциальных уравнений второго порядка. Для того чтобы решение полученных уравнений было единственным, к ним следует добавить 2 начальных условия. Для этого ряд Фурье функции u(x; t), а также ряды Фурье функций '(x) и

(x) подставим в начальные условия:

+1

+1

XX

ck(0)yk(x) = 'kyk(x);

k=1	k=1
+1	+1

XX

c0k(0)yk(x) = kyk(x):

k=1				k=1
Отсюда ck(0) = 'k и ck0 (0) =		k.
Таким образом, для функций ck(t) получилась задача Коши
8ck		(0)	= 'k;
>	ck00	(t) =		a2 k2ck(t);
<c0		(0)	=	k:
> k
:

Общее решение дифференциального уравнения

ck(t) = A1;k cos(a kt) + A2;k sin(a kt):

Подставим эти функции в начальные условия: ck(0) = A1;k = 'k;

ck0 (0) = a kA2;k =

k

A2;k =

k

:

a k

Тогда

ck(t) = 'k cos(a kt) +

k

sin(a kt):

a k

В итоге получим решение задачи (3.8)–(3.10):

+1

a kt

l

a kt

sin

kx

: (3.12)

u(x; t) = k=1

'k cos l + a kk sin l

l

X

97

и фазой k. Частоты !k

Исследуем найденное решение. Коэффициенты ck(t) можно преобразовать:

ck(t) = Fk sin

a kt

+ k ;

(3.13)

l

sin =

'k

;

2

k

:

>cos k =

<

Fk

2

k

8

где Fk = s'k

+

a k2

и

k

Следовательно, функция

:

u(x; t) представима в виде

>

a kFk

+1

Fk sin

a kt

kx

u(x; t) = k=1

l

+ k sin

l :

X

a kt

kx

Слагаемые ряда Фурье ck(t)yk(x) = Fk sin

+ k sin

на-

l

l

зываются стоячими

волнами. Для

любой

фиксированной

точки x

(x 2 (0; l)) струны решение представляет собой сумму бесконечного числа стоячих волн. Каждая стоячая волна – это синусоида, амплитуда которой

	Fk sin	kx		зависит от выбранной точки струны x.
		l
	На отрезке [0; l] для каждой k-й стоячей волны можно выделить точки,
	в которых sin			kx	= 0:
				l
					xn =	nl	(n = 1; 2; :::; k 1):
						k

Точки xn называются узлами стоячей волны. В этих точках соответствую-

щая стоячая волна будет неподвижной. Точки, в которых sin			kx	= 1:
			l
xm =	(2m 1)l	(m = 1; 2; :::; k);
	2k

называются пучностями стоячей волны. В точках xm k-я стоячая волна совершает колебания с наибольшей амплитудой.

Из равенства (3.13) следует, что каждая стоячая волна совершает ко-

лебания с одной и той же частотой !k = ka l

называются собственными частотами струны. Наименьшей собственной частотой будет

!1	= la		= l s
					;
					T

где T – натяжение; – плотность струны.

98

Из полученной формулы видно, что чем больше натяжение струны T
и чем короче и легче струна (т. е. чем меньше l и ), тем больше частота
колебаний струны !1, а значит, тем выше будет звук, издаваемый струной.
Применим теперь полученное решение уравнения колебаний струны
для конкретных задач.
Пример 3.5. Найти поперечные колебания струны с закрепленными
концами x = 0 и x = l, если начальная форма струны – это парабола
(рис. 3.9) с наибольшим отклонением h, а начальная скорость точек струны
равна нулю.
Согласно условиям задачи '(x) =
4h	и			0. Функция
l2 x(x l)		(x)	=			U
u(x; t), описывающая поперечные колеба-							H
ния струны, являющаяся решением зада-
чи (3.8)–(3.10), представляется в виде ря-
да Фурье (3.12). Найдем коэффициенты
Фурье 'k и	k функций '(x) и				(x) со-	0	L	X
ответственно:							Рис. 3.9

'k =	('(x); yk(x))	;	k =	( (x); yk(x))	:
	kyk(x)k2			kyk(x)k2
Вычислим сначала квадрат нормы функции yk(x):
			l	l	sin2		l	dx =	2:
	kyk(x)k2 = Z0			yk2(x)dx = Z0
							kx			l

Скалярное произведение функций '(x) и yk(x) получим по правилу:

('(x); yk(x)) = Z0	l		(x2	lx) sin	l	dx:
		l2
		4h			kx

Дважды проинтегрировав по частям, придем к равенству

8hl 1 ( 1)k ('(x); yk(x)) = 3k3 :

Очевидно, что ( (x); yk(x)) = 0. Таким образом, все k = 0, а 'k вычисляются по формулам

'k =	16	1 3k3	1)k		(k = 1; 2; :::):
	h	(

99