Транспортная Эконометрика(Ивченко) Шпоры
.docx
Эконометрика как наука выделилась и сформировалась в результате синтеза 3 наук: статистики, математики и экономической теории. Эконометрика – наука о моделировании экон. явлений и процессов, которая позволяет объяснять и прогнозировать их развитие. Предметом изучения эконометрики является количественное выражение взаимосвязи экономических явлений и процессов. Цель эконометрики – разработка способов моделирования и количественного анализа, реальных экон. явлений, процессов, объектов. Задачи эконометрики:
Например: y = x / a – модель; x,y – переменные; а – параметр.
Каким образом происходит взаимосвязь 3 названных дисциплин? Всё начинается с экономической теории. На её основе разрабатываются общие концепции развития изучаемых экон. явлений и процессов, выявляющиеся объективно существующие экон. законы и связи. С помощью статистики – эти экон. процессы измеряются и выражаются в конкретных количественных показателях. Математический инструментарий эконометрики позволяет строить матем. модели экон. процессов, оценивать параметры этих моделей и оценивать качество модели. При интерпретации полученных результатов моделирования вновь первостепенную роль играет экон. теория. История развития эконометрики: В качестве самостоятельного научного направления эконометрика выделилась в конце 20 гг. 20 века. Сам термин «эконометрика» был введён в научный оборот в 1926 г. норвежским учёным Флишем. В 1930 г. было образованно эконом. сообщество «Международный Союз Экономистов», главной целью которого было обозначено использование статистики и математики для развития экон. теории. Первым Президентом этого общества был американский экономист Фришер. Экон. сообщество издаёт журналы «Эконометрика» и т.д., а с 1978 г. присуждает одну из престижных экон. премий. Путь эконометрики в нашу страну был сложен. Первая попытка внедрить эконометрику в современную науку , привела к выделению таких направлений, как экон. матем. методов и экон. кибернетики. По-настоящему эконометрика стала развиваться в России лишь в середине 90 гг.
|
2. Эконометрическая модель как основа механизма эконометрического моделирования. Классификация эконометрических моделей. Модель – объект, созданный исследователем для анализа и изучения объекта – оригинала и сохранения его существующих характеристик. Например, глобус – модель земного шара. Моделирование – процесс построения, изучения и применения моделей. Эконометрическая модель – вероятно-статистическая модель, описанная механизмом функционирования экон. явлений и процессов. В общем виде эконометрическую модель можно представить в следующем виде: y = f (x) + ε y – наблюдаемое значение зависимой переменной; f (x) – объяснённая часть зависимой переменной, которая зависит от значений объясняющих независимых переменных х; ε – случайная составляющая y – зависимой переменной (ошибка возмущения модели). Таким образом, эконометрическая модель представляет собой математическую формулу, зависимость результативной переменной y от независимой переменной х (факторной переменной). При эконом. моделировании перед исследователем стоят задачи:
Эконометрическая модель является главным инструментом эконометрики. Существуют 3 класса эконометрических моделей: 1). Регрессионные модели с одним уравнением – зависимая или объяснённая переменная, представленная в виде функции от факторных или объяснённых переменных х: y = f (х1, х2,…,хk) + ε В зависимости от количества факторных приз-в различают:
Модели бывают:
Приведём пример регрессионных моделей с одним уравнением:
|
3. Типы данных и виды переменных в эконометрических исследованиях экономических явлений. Типы статистических данных:
Примеры:
Примеры: все теже самые сведения, только по одной фирме за несколько одинаковых периодов времени. y – зав-я переменная, результаты, объяснённая переменная, либо в роли фактора х – независимая объяснённая переменная. Переменные участвуют в эконометрической модели y = f (x) + ε делятся на следующие виды: 1). Текущие, экзогенные(независимые – х) – заданные из вне модели, значение которых определяется в данный момент времени. хt , t – текущий; 2). yt – текущие, эндогенные (зависимые переменные), заданные внутри модели. 3). Лаговые экзогенные (х t-1, х t-z,…,хt)k ; эндогенные (y t-1, y t-z,…,yt)k ; датированные предыдущим периодом времени. 4). Предопределённые переменные.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4. Этапы эконометрического моделирования. 1). Теоретический или постановочный – в его ходе формулируется цель, обозначается объект исследования, определяется круг участвующих в моделировании эконом. характеристик. 2). Информационный – в его ходе осуществляется поиск требуемых данных, проверка их достоверности и сопоставимости. 3). Спецификация моделей (построение эконометрической модели): y = f (x) + ε – общий вид эконометрической модели; y = a + bx + ε/ Непосредственное построение эконометрической модели, выраженная взаимосвязь между экзогенными (независимые переменные –х) и эндогенными переменными (внутри модели – y). 4). Идентификация моделей – статистический анализ и оценка качества модели и её параметров. 5). Верификация – проверка адекватности модели реальному экономическому явлению, оценка качества расчётов и прогнозов, сделанных на основе моделей. (x' – y' – отличается от реального y на ε).
|
5. Понятие функциональной и статистической зависимостей. Этапы проведения комплексного корреляционно – регрессионного анализа. Функциональная зависимость – связь, при которой каждому значению х соответствует точно определённое значение y. Например, зависимость между площадью и стороной квадрата. Статистическая зависимость – связь, при которой каждому значению независимой переменной х соответствует множество значений зависимой переменной y, причём неизвестно заранее, какое именно примет значение y. х : y1, y2, y3, yр .
|
6. Понятие парной, частной и множественной корреляции. Расчёт и интерпретация коэффициента корреляции для парной линейной регрессии. Корреляция – статическая зависимость между случайной величиной х и y, при которых изменение одной из случайных величин (х) приводит к изменению мат. ожидания другой (y). Различают 3 вида корреляции:
Для расчёта парного линейного коэффициента корреляции, можно воспользоваться следующей формулой: rx y = (x̄ȳ - x̄∙ȳ)/σx∙σy x̄ȳ = ∑xy/n Коэффициент корреляции принимает значение [-1;1]. Положительный знак коэффициента корреляции –прямая связь, отрицательный – обратная, если r = +-1, то связь между признаками - линейная (функциональная). Если r = 0 – линейная связь между х и y отсутствует. Если r = 0,….,0.3 – практически нет связи, от 0.3 до 0.5 – слабая связь, от 0.5 до 0.7 – умеренная, от 0.7 до 0.9 – сильная линейная связь, от 0.9 и до 1 – очень сильная линейная связь. Коэффициент корреляции в единственном числе r, как статическая величина, подвергшаяся оценке на достоверность. Это объясняется тем, что любая совокупность наблюдений представляет некую выборку; следовательно, значение любого показателя, вычисленное на основе выборки, не может рассматриваться как истинное, а является только более или менее точной его оценкой. В связи с этим возникает необходимость проверки существенности или значимости показателей. Для оценки значимости r, используют Критерий Стьюдента: tрасч = rxy ( (n – k – 1)/(1 – rxy2) )1/2 k – Число фактических признаков, включённых в модель или исследования; x – фактический признак; y – результативный признак. tрасч = ( (r2/(1 – rxy2))∙(n – 2) )1/2 – формула при k = 1, т. е. парной корреляции.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
7. Дисперсионный анализ: сущность и методика проведения. Правило сложения дисперсий. Коэффициент детерминации и его характеристика. Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной y от среднего значения y раскладывается на две части – «объяснённую» и «необъяснённую». Σ (y – y̅)2 = Σ (ŷx – y)2 +Σ (y - ŷx)2 Где: Σ (y – y̅)2 – общая сумма квадратов отклонений; Σ (ŷx – y)2 – сумма квадратов отклонений, объяснённая регрессией (или факторная сумма квадратов отклонений); Σ (y - ŷx)2 – остаточная сумма квадратов отклонений, характеризующая влияние неучтённых в модели факторов. Схема дисперсионного анализа имеет вид, представленный в таблице (n- число наблюдений, m – число параметров при переменной х):
Сопоставляя факторную и остаточную дисперсии в расчёте на одну степень свободы, получим величину F - критерия Фишера: F = Dфакт/Dост Фактическое значение F – критерий Фишера сравнивается с табличным значением Fтабл (α, k1, k2) при уровне значимости α и степенях свободы k1 = m и k2 = n – m - 1/ При этом если фактическое значение F – критерия Фишера больше табличного, то признаётся статическая значимость уравнения в целом. |
8. Спецификация модели парной линейной регрессии. Спецификация модели – формулировка вида модели исходя из соответствующей теории связи между переменными. Парная линейная регрессионная модель – наиболее простой вид эконометрической модели, в которой рассматривается зависимость объясняемой переменной y только от одной объясняющей переменной х (поэтому модель называется парной), причём эта зависимость линейная. Эта модель имеет вид: y = f(x) y = ŷ + ε – связь между параметрами; y – фактическое значение результативного признака; ŷ – теоретическое значение результативного признака, найденное исходя их уравнения регрессии; ε – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии. Случайная величина ε называется также возмущением. Она включает влияние не учтённых в модели факторов, случайных ошибок и особенностей измерения. От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака ŷ подходит к фактическим данным y. К ошибкам спецификации относится неправильный выбор той или иной математической функции для ŷ и недоучёт в уравнении регрессии какого-либо существенного фактора, т. Е. использование парной регрессии вместо множественной. Наряду с ошибками спецификации могут иметь место ошибки выборки, которые имеют место в силу неоднородности данных в исходной статистической совокупности, что, как правило, при изучении эконометрических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла.
|
9. Оценка параметров парной линейной регрессии и их экономическая характеристика. Построение линейной регрессии сводится к оценке его параметров а и b. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов. МНК позволяет получить такие оценки параметров а и b,при которых сумма квадратов отклонений фактических значений результативного признака y от теоретических ŷ минимальна: Σ (yi - ŷxi)2 = Σε2i →min Чтобы найти минимум рассматриваемых функций, надо вычислить частные производные по каждому из параметров а и b и приравнять их к нулю. Обозначим Σε2i через S, тогда: S = Σ (yi - ŷx)2 = Σ(y – a – bx)2 dS/da = -2Σy + 2na+ 2bΣx = 0 dS/db = -2Σy + 2aΣx+ 2bΣx2 = 0 После несложных преобразований, получим следующую систему линейных уравнений для оценки параметров а и b: an + bΣx = Σy aΣx + bΣx2 = Σxy Решая данную систему уравнений, найдём искомые оценки параметров а и b. Можно воспользоваться следующими готовыми формулами, которые следуют непосредственно из решения системы: a = y̅ - bx̅ и и = cov (x, y)/σ2x Поскольку cov (x, y) = x̅y̅ - x̅ ∙ y̅ - ковариация признаков х и y и σ2x = х̅2 - х̅ 2 – дисперсия признака х. Получим следующую формулу расчёта оценки параметров b: b = (x̅y̅ - x̅ ∙ y̅)/( х̅2 - х̅ 2) где: x̅ = 1/n Σx, y̅ = 1/n Σy, х̅2 = 1/n Σx2, x̅y̅ = 1/n Σxy Ковариация – числовая характеристика совместного распределения двух случайных величин. а и b можно рассчитать с помощью функции ЛИНЕЙН, задав значения х и y. Σyi = Σŷi
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3. |
y – цена товара; х1 – объём поставок; х2 – цена конкурентного товара на рынке.
y – объём продаж; х1 – цена единицы товара; х2 – цена конкурентных товаров; х3 – реальный доход потребителей.
Q = α∙Kβ∙α1-β – классическая производная функция; y = α∙x 1β∙x 21-β – модель. α, β – параметры (Const) 2). Модели временных рядов – зависимость y от временных рядов (от течения времени). Этот класс делится на подклассы:
а). Модель тренда: y (t) = T' (t) + ε ; T (тренд) – тенденция или устойчивое изменение уравнения изучаемых явлений с течением времени; б). Модели сезонности: y (t) = S (t) + ε ; Эту модель характеризуют устойчивые внутригодовые колебания уровня показат. результативного признака. в). Модель тренда и сезонности, которые могут быть аддитв-ой, т.е. y (t) = T (t ) + S (t) + ε ; или мультипликационной, т.е. y (t) = T (t ) ∙ S (t) + ε ;
а). Пред – ие значения факторных признаков: y = f (х t-1, х t-z,…,хt-k); б). Предыдущие значения y: y t = f (y t-1, y t-z ,…, y t-k); в). Будущих значений факторных и результативных признаков: y t = f (х t+1, х t+2,…,y t+1, y t+2); 3). Системы одновременных уравнений – состоят из тождеств (т.е. равенств) и регрессионных уравнений, в которых наряду с факторными признаками вкл. результативные признаки их других уравнений системы. Примером системы одновременных уравнений является модель спроса и предложения, вкл. 2 регрессионных уравнения и 1 тождество: QtS = a0 + a1∙Pt + a2∙Pt-1 QtD = b0 + b1∙Pt + b2∙Ut Qt = QtD Q – объём; t – время; S – предложения; D – спрос; Pt , Pt-1 – цена товара в момент времени t и в предыдущий момент времени (t-1); U t – доход потребителя в момент времени t; Данная модель объясняет две результативные переменные: Qt – объём спроса равен объёму предложения в момент времени t; Pt – цена товара в момент времени t; a0, a1, a2, b0, b1, b2 – параметры эконометрических моделей (Сonst).
|
1. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
6. |
5. |
4. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
9. После нахождения параметров а и b записывают уравнение регрессии: y = a + bx + ε Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Формально параметр а значение y при х = 0. Если признак – фактор х не может изменить нулевого значения, то вышеуказанная трактовка свободного члена а не имеет смысла, т. е. параметр а может не иметь экономического содержания. В уравнении линейной регрессии параметр а с математической точки зрения определяет среднее значение y, которое складывается под влиянием всех факторов, кроме х (обнуляем х).
|
8. Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя формулу модели(вид математической формулы), а ошибки выборки – увеличивая объём исходных данных, то ошибки изменения практически сводят на нет все усилия по количественной оценке связи между признаками. В парной регрессии выбор вида математической функции ŷ = f(x) может быть осуществлён тремя методами:
|
7. Для парной линейной регрессии m = 1, поэтому: F = Dфакт/Dост = ( Σ (ŷx – y̅)2/ Σ (y - ŷx)2) ∙ (n – 2) Величина F – критерия связана с коэффициентом детерминации R2xy, и её можно рассчитать по формуле: F = (R2xy /(1 - R2xy) ) ∙ (n – 2). Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции R2xy, называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака y, объясняемую регрессией, в общей дисперсии результативного признака: R2xy = σ2объясн/σ2y = 1 - σ2ост/σ2y Где: σ2ост = 1/n Σ (yi - ŷi)2 σ2y = 1/n Σ (yi - y̅)2 = y̅2̄ - y̅ 2 Теоретически возможный коэффициент детерминации: 0≤ R2xy ≤ Чем ближе R2xy к 1, тем качество модели выше, тем ближе в совокупности линия к экспериментальным точкам. Практически допустимы модели с R2xy˃0.8.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
10. Интервалы прогноза по линейному уравнению регрессии. Средняя ошибка аппроксимации. Прогнозирование с применением уравнения регрессии: если уравнение регрессии признано адекватным, то переходят к построению прогноза. Yпрогноз получается при подстановке в уравнение регрессии ожидаемой величины х. yˆпрогн = a + bxпрогн Данный прогноз называется точечным. Вероятность реализации точечного прогноза не высока, поэтому рассчитывается доверительный интервал прогноза с достаточной степенью надёжности. yˆпрогн - < yпрогн < yˆпрогн + Доверительный интервал: Если tтабл < tфакт, Н0 отклоняется, т.е. a, b и rху не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Для расчета доверительного интервала определяем предельную ошибку ∆ для каждого показателя: Dа = tтабл ma, Db = tтабл mb. Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное и отрицательное значения.
|
Соотношение между социально – экономическими явлениями не всегда можно выразить линейными функциями. Часто пользуются нелинейной регрессией. Различают 2 класса нелинейных регрессий:
Регрессии нелинейные по включённым переменным приводятся к линейному виду простой заменой переменных, а дальнейшая оценка параметров производится с помощью метода наименьших квадратов. Как показывает практика чаще всего используются квадратичная модель (парабола второй степени), в отдельных случаях – полином третьего порядка. В эконометрике также в классе нелинейных функций, параметрами которых оцениваются МНК, известна равносторонняя гипербола yˆ = a + b/x. Примером является кривая Филлипса, характеризующая нелинейное соотношение между нормой безработицы х и процентом прироста зарплаты y: yˆ= a + b/x + ε. Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях широко используется степенная функция y = abx + ε, где b – коэффициент эластичности. Для нахождения параметров а и b в exel, пользуются функцией (=ЛИНЕЙН), задавая в качестве объяснённой переменной исходные значения y. Этот приём называется линеаризацией. Рассмотрим примеры линеаризации некоторых нелинейных моделей 2 класса. Самыми распространёнными среди таких функций является степенная и показательная функции. Для определения параметров степенной функции yˆ= axbε (случ. ε мультиплик-но (перемножение) связанное с х (фактическим признаком), необходимо привести у линейному виду путём логарифмирования обеих частей уравнения.
|
12. Расчёт индекса корреляции для парной нелинейной регрессии. Тесноту связи между рассматриваемым набором факторов x1, x2,…,xm и исследуемым признакам y в линейной и нелинейной множественной регрессии характеризует индекс множественной корреляции ( или совокупный индекс корреляции). Для нелинейной множественной регрессии он рассчитывается так: Ryx1, x2…xm = (1 – σ2ост/σ2y)1/2 = (1 - ∑(yi - yˆx1, x2…xm)2/∑(yi - ȳ)2)1/2 Где: σ2ост – остаточная дисперсия для уравнения y = f(x1, x2…xm); σ2y – общая дисперсия результативного признака. Границы изменения индекса множественной корреляции от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции: Ryx1, x2…xm ≥ Ryxi (max)(i = 1̄,m¯).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
13. Общий, средний и точечный коэффициент эластичности для моделей парной нелинейной регрессии. Помимо индексов коэффициента корреляции и детерминации оценить тесноту связи между х и y можно с помощью коэффициента эластичности. Общий коэффициент эластичности показывает насколько % изменится результативный признак y при изменении и факторного на 1 %. Э = y'(x) x/y y'(x) – производная функции y (x). Коэффициент эластичности часто рассчитывается для среднего значения ч по формуле: э̄ = y'(x) x̄/ȳ Средний коэффициент эластичности характеризует процентное изменение y относительно своего среднего значения при изменении х на 1 % относительно своего среднего значения. Для параболы средний коэффициент эластичности равен: э̄ = (b + 2cx̄)x̄/ȳ y = a + bx + cx2 y = a + b, э̄ = -b/(ax̄ + b) y = abx, э̄ = x̄lnb y = axb, э̄ = b
|
14. Понятие множественной регрессии и корреляции. Задачи множественного корреляционно – регрессионного анализа. Модель множественной регрессии – уравнение, отражающее корреляционную связь между результатом и несколькими факторами. В общем виде: y = f(x1, x2…xp,ε) y – зависимая, моделируемая переменная, результат; x1, x2…xp – факторы, зависимые переменные, экзогенные; f – функция. В качестве функции f для множественной регрессии часто выбирают наиболее простые – линейную, степенную, показательную. Y = a + b1x1 + b2x2 + … + bpxp + ε Множественная регрессия применяется при исследованиях спроса и потребления, доходности акций, изучения функций издержек и производства и т.д. Множественная регрессия – один из наиболее распространённых методов в эк-ке. Цель – построение модели с большим числом факторов и определение влияния каждого в отдельности, а т. ж. их совокупного влияния на y. Множественная корреляция занимается изучением, измерении связи между результативным признаком, двумя и более факторными. Множественная корреляция определяет: 1. форму связи; 2. тесноту связи; 3. влияние отдельных факторов на общий результат. Задачи множественного корреляционно – регрессионного анализа:
|
15. Отбор факторных признаков при построении модели множественной регрессии. При отборе факторов существуют правила. Включение в уравнение регрессии тех или иных факторов связано с представлением исследователя о природе взаимосвязи с другими эконом. явлениями, т. е. он должен иметь определённые эконом. Знания, позволяющие делать вывод о наличии сильной связи между х и y. Факторы должны отвечать требованиям:
r x1, x2 = (x̄1x̄2 - x̄1 ∙ x̄2)/σx1 ∙ σx2 Существование корреляционной связи между х может быть выевленно с помощью показателей корреляции; между ними в частном с помощью парного множественного коэффициента корреляции. Можно записать в виде матрицы:
rxi xi = 1 – коэффициент корреляции с самим собой; rxi xj = rxj xi Данная матрица является симметричной, поэтому в ней указывается главная диагональ и элементы под ней.
Если парный линейный коэффициент корреляции между двумя х > 0,7; то один из этих х должен быть исключён из модели. Как правило исключается тот х, чей r и y меньше.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
16.Понятие мультиколлинеарности и способы ее устранения. Матрица парных линейных коэффициентов корреляции. Мультиколлинеарность – связь между несколькими факторами Х, включенными в модель. Ее наличие можно подтвердить, найдя определитель матрицы парных коэффициентов корреляции. Если связь между факторами отсутствует, то определитель матрицы равен 1. Если связь тесная – стремится к 0. Мультиколлинеарность в эконометрических моделях необходимо устранять, т.к она искажает модель. Причины возникновения мультиколлинеарности между Х:
Методы устранения или уменьшения мультиколлинеарности.
ŷ = a + b1x1 ŷ = a + b1x1 + b2x2 ŷ = a + b1x1 + b2x2 + b3x3
Уравнения регрессии вводят численные значения и исключают незначимые факторы. Процесс исключения факторов может продолжаться до тех пор, пока модель не станет удовлетворять условия.
|
17. Оценка параметров множественной регрессии. Параметры уравнения множественной регрессии (а,b1,b2…) определяются как и при парной с помощью МНК. Суть этого метода заключается в минимизации суммы квадратов(отклонений)отношений У фактического от У теоретического. S = Σ(Yi - ŷ)2=Σ(Yi – (a + b1x1 + b2x2 + … + BnXn))2→min В уравнении неизвестными являются параметры уравнения регрессии. Чтобы их найти дифференцируют сумму S по этим переменным и приравнивают к нулю. Факторы:
Получим систему уравнений, решение которой позволяет определить параметры системы. Уравнение множественной линейной регрессии называется моделью в натуральной форме. Если провести стандартизацию переменных, т.е выполнить следующие преобразования: ty =(Yi-Ӯ)/σy txi=(Xi – X(с черточкой горизонтальной сверху))/σх
ty = β1*tx1 + β2*tx2 + β3*tx3 +U U – ошибка Коэффициенты модели стандартной формы отличаются от коэффициентов в натуральной форме. Определить β коэффициенты можно с помощью МНК. Применяя его к уравнению множественной регрессии в стандартизированном масштабе после соответствующих преобразований получаем систему нормальных уравнений следующего вида(система решаема):
rx1y
= β1
+ β2rx1x2
+ … + βprx1xp rx2y = β1rx2x1 + β2 + … + βprx2xp … rxpy = β1rxpx1 + β2rxpx2 + … + βp
|
18. Множественная корреляция. Индексы корреляции и детерминации и их характеристика. Корреляция – статистическая зависимость между случайными величинами Х и У, при которой изменение одной случайной величины (Х) приводит к изменению другой(У). Множественная корреляция – связь между одним У и двумя и более Х, включенными в исследовании. Экономические явления определяются большим числом факторов одновременного и совокупного воздействуя на У. В связи с этим возникает задача исследования зависимости У от нескольких х1,х2…, которые может быть решена с помощью множественного корреляционно-регрессионного анализа. Модель множественной регрессии – это уравнение, отражающее корреляционную связь между результатом и несколькими факторами. В общем виде: у = f(x1,x2…xn,E(ипсилон)). Y – моделированная переменная; Х – независимая переменная. В качестве функции для множественной регрессии выбирают линейную: у = a + b1x1 + b2x2 + … + E(ипсилон) a, b1, b2 - параметры. Множественная регрессия широко применяется для определения Спроса и Предложения и т.д В настоящее время множественная регрессия один из наиболее распространенных методов в экономике. Его главная цель заключается в построении модели с большим числом факторов и определении при этом влияния каждого из них в отдельности, а также совокупного влияния каждого из них на У. Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата - коэффициента детерминации. R2показывает долю вариации У, находящуюся под воздействием Х, т.е определяет какая доля вариации У учтена в модели и обусловлена влиянием на У факторных признаков Х, включенных в модель. R2 = (σ2объясŷ)/σ2у=Σ(Yi - Ӯ)2/Σ(ŷi - Ӯ)2=1-(σ2остε/σ2у) εi =Yi - ŷi Множественный коэффициент корреляции может быть найден так:
R
=
Чем ближе R→1, тем теснее связь между результатом и всеми факторами, а уравнение регрессии лучше описывает фактические данные. Значение коэффициента множественной корреляции больше или равно величине максимального коэффициента корреляции. R2yx1,x2…xk≥│rxy(max)│ rxy= (xy(общая черта над ними) – y*x(по одной черточки над каждой))/σх*σу |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
12. |
11. ln y = ln a + b ln x + ln ε ln y = Y ln a = A Y = A + bX + E или Yˆ = A + bx ln x = X ln ε = E Для нахождения параметров А и b воспользуемся функцией ЛИНЕЙН, задавая в качестве объясняющей переменной Х, а в качестве объясняемой Y. Внутри функции ЛИНЕЙН заложен МНК. a = eA Показательная функция y= axbε также может быть подвергнута линеаризации: С помощью ексель « =EXP(A)» - функция ексель.
|
10. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
15. |
14. |
13. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
18. Для линейной множественной регрессии коэффициент множественной корреляции рассчитывается: R2yx1,x2…xk= βxi – стандартизированные коэффициенты регрессии; ryxi – парные коэффициенты корреляции результата с каждым фактором. Множественный коэффициент детерминации:
Ryx1,x2…xk= Определитель полной матрицы парных коэффициентов корреляции, т.е включая парные линейные коэффициенты корреляции факторов с результатом и между собой.
|
17. Решить систему можно методом определителей(Крамера) βi =∆i/∆ C уравнением регрессии в стандартном масштабе работать удобно, т.к парные линейные коэффициенты r рассчитываются еще методом отбора факторов: bi = βi * σy/σxi σy – среднее квадратическое отклонение по У; σxi – среднее квадратическое отклонение по определенному Х. Параметр а равен: a= Ӯ – b1x(с чертой наверху)1 – b2x(с чертой)2 - … - bpxn Существует другой способ нахождения параметров линейной множественной регрессии. Он также заключается в формировании матрицы:
|
16. Существование корреляционной связи между Х может быть выявлено с помощью показателей корреляции между ними, в частности, с помощью парного линейного коэффициента корреляции.
Коэффициент корреляции фактора с самим собой равен 1. rx1x2 = 1 Коэффициент корреляции I –го фактора с j-м равен коэффициенту корреляции i с j. Следовательно, матрица симметрична, поэтому в ней указывается главная диагональ и элементы под ней:
Если парный линейный коэффициент корреляции между 2-мя Х больше 0,7, то один из них должен быть исключен из модели, как правило исключается тот Х, чей rxpу меньше. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Значения параметров будут находиться в ячейках матрицы В:
Матрица В определяется: В = (XT * X)-1XTY XT – транспонированная матрица =ТРАНСП XTX – произведение соответствующих матриц = МУМНОЖ (XTX)-1 –обратная матрица = МОБР XT Y – МУМНОЖ (XT * X)-1XTY = МУМНОЖ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
19.Множественная и частная корреляция. Расчет множественного и частного коэффициентов корреляции для множественной линейной регрессии. Корреляция – статистическая зависимость между случайными величинами Х и У, при которой изменение одной случайной величины (Х) приводит к изменению другой(У). Множественная корреляция – связь между одним У и двумя и более Х, включенными в исследовании. Частная – связь между 2мя признаками Х и У при фиксированном значении других Х. В зависимости от количества Х-в различают:
Тесноту связи между рассматриваемым набором факторов и исследуемым признаком У в линейной и нелинейной множественной регрессии характеризует индекс множественной корреляции. Для нелинейной множественной корреляции он рассчитывается так:
Ryx1x2…xn
=
(2 – это в квадрате) σ2ост – остаточная дисперсия для уравнения y = f(x1,x2…xn) σ2y - общая дисперсия результативного признака. Границы изменения индекса множественной корреляции от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции: R2yx1,x2…xk≥│rxy(max)│ При линейной зависимости признаков формула индекса корреляции может быть представлена: R2yx1,x2…xk= βxi – стандартизированные коэффициенты регрессии; ryxi – парные коэффициенты корреляции результата с каждым фактором. Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии. В общем виде при наличии m факторов в уравнении множественной регрессии коэффициент частной корреляции, измеряющий влияние на У произвольного фактора xi, при неизменном уровне других m-1 факторов определяются:
ryx1*x1x2…xi-1xi+1…xm=
Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается.
|
20.Показатели силы связи в модели множественной регрессии. Расчет и характеристика коэффициентов эластичности для модели множественной регрессии
|
21.Прогнозирование по уравнению множественной регрессии. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
22. Сущность МНК для оценки параметров парной и множественной регрессии. |
23.Гетероскедастичность остатков. Тесты проверки на гетероскедастичность и их характеристика. |
24.Понятие , виды и компоненты временного ряда. Эконометрическое моделирование временных рядов(рядов динамики). В качестве источников инфы в эконометрике широко используются ряды динамики(РД). РД - это значения, изучаемого показателя, расположенных в хронологическом порядке. Отдельные значения - уровни РД. РД состоит из 2-х элементов: время t и уровни У. Модели по РД могут строиться на основе:
РД классифицируют по следующим признакам:
Уровни РД в конкретный период или момент времени принимают те или иные значения в результате действия разных факторов. В связи с этим фактическую величину уровня ДР можно представить как функцию (зависимость) 3-х компонентов: T – тенденция ряда(тренд) – обусловленный влиянием регулярных основных факторов, действующих на регулярных явлениях. Р – периодические колебания, вызванные особенностями явления в один период времени по сравнению с другими. Бывают циклические (можно проследить за пределы года ) и сезонные (прослеживаем в течении сезона, цикла). Е (ипсилон) – случайные колебания. Символически это можно представить так: у = f(T; P; E(ипсилон)). Yt - фактический уровень РД, зависит от T;P;E(ипсилон). Рассмотрение компоненты РД не обязательно присущи каждому РД.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
25.Аддитивная и мультипликативная модель временного ряда(ряда динамики - РД). РД - это значения, изучаемого показателя, расположенных в хронологическом порядке. Отдельные значения - уровни РД. РД состоит из 2-х элементов: время t и уровни У. Модель РД может быть представлена:
Модель РД с Т и с аддитивной сезонностью имеет место в том случае, если сезонность колебания не зависят от уровней или значения ряда (y = T + S + E(ипсилон)). Модель РД с Т и мультипликативной сезонностью имеет место в том случае, когда сезонные колебания зависят от уровней ряда (y = T * S + E(ипсилон)). Основная задача эконометрического исследования РД – выявление и придания количественного значения(выражения) каждому из вышеперечисленных компонентов.
|
26.Автокорреляция уровней временного ряда(ряда динамики-РД). При наличии тенденции в РД каждый последующий уровень ряда зависит от следующего. Эта зависимость называется АВТОКОРРЕЛЯЦИЕЙ. Коэффициент корреляции 1-го порядка: _____________________________________ r = (Yt*Yt-1- Yt*Yt-1) Yt-первый массив; Yt-1 – тот же массив, но сдвинутый на одну ячейку. Коэффициент корреляции 2-го порядка: ___________________________________ r = (Yt*Yt-2- Yt*Yt-2) Общая формула коэффициента автокорреляции: ___________________________________ r = (Yt*Yt-τ- Yt*Yt-τ) τ – величина лага(шага-сдвига) Максимальная величина лага не должна превышать n/4, где n – количество уровней ряда. Серию коэффициентов с последующим увеличением величин лага называют автокорреляционной функцией (= АКФ), а ее графическое изображение – коррелограммой. А К Ф дает представление о внутренней структуре РД. С помощью АКФ наличие или отсутствие в РД периодических колебаний и величину периода колебаний. Она равна той величине лага, при которой коэффициент автокорреляции наибольший. Определив несколько последующих коэффициентов автокорреляции, можно выявить лаг, при котором автокорреляция наиболее высока. Выделяют следующие основные положения анализа структуры: -если наиболее высоким окажется значение автокорреляции 1-го ряда, то известный ряд содержит только тренд. -если наиболее высоким окажется значение автокорреляционного порядка τ, то кроме тренда будет и периодические колебания.
|
27. Автокорреляционная функция и ее использование в определении компонентов временного ряда(ряда динамики-РД). При наличии тенденции в РД каждый последующий уровень ряда зависит от следующего. Эта зависимость называется АВТОКОРРЕЛЯЦИЕЙ. Формулу см. шпора №26. Серию коэффициентов в последующим увеличением величин лага называют автокорреляционной функцией (= АКФ), а ее графическое изображение – коррелограммой. А К Ф дает представление о внутренней структуре РД. С помощью АКФ наличие или отсутствие в РД периодических колебаний и величину периода колебаний. Она равна той величине лага, при которой коэффициент автокорреляции наибольший. Определив несколько последующих коэффициентов автокорреляции, можно выявить лаг, при котором автокорреляция наиболее высока. Выделяют следующие основные положения анализа структуры: -если наиболее высоким окажется значение автокорреляции 1-го ряда, то известный ряд содержит только тренд. -если наиболее высоким окажется значение автокорреляционного порядка τ, то кроме тренда будет и периодические колебания.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
21. |
20. |
19. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
24. Могут быть РД,
где нет тренда или периодических
колебаний. А может и то и другое
отсутствовать. В этом случае символически
это можно записать так: Y
t
= f(E(ипсилон)).
Уровни такого РД являются функции
случайной составляющей. Они колеблются
вокруг среднего значения уровня, что
характерно для так называемого
стационарного ряда. На графике такой
ряд представляет собой ломаную линию
параллельную оси Х
Такие ряды редки в экономике. Чаще имеют место ряды с тенденцией, хотя ряды без тенденции наблюдаются при изучении динамики показателей из относительных и средних величин. Часто РД в экономике характеризуются тенденцией и случайными колебаниями. Модель такого ряда может иметь вид: у = f(T) + E(ипсилон), где f(T) – математическая зависимость, характеризующая закономерность развития явления во времени:
При изучении динамических явлений за продолжительный период времени уровни ряда могут обнаруживать периодические колебания, т.е повторяющиеся спады и подъемы. Модель РД может быть представлена:
Модель РД с Т и с аддитивной сезонностью имеет место в том случае, если сезонность колебания не зависят от уровней или значения ряда (y = T + S + E(ипсилон)). Модель РД с Т и мультипликативной сезонностью имеет место в том случае, когда сезонные колебания зависят от уровней ряда (y = T * S + E(ипсилон)). Основная задача эконометрического исследования РД – выявление и придания количественного значения(выражения) каждому из вышеперечисленных компонентов.
|
23. |
22. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
27. |
26.
|
25. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
28.Основные типы трендов временных рядов(рядов динамики - РД) и их распознавание. Построение модели тенденции (уравнение тренда) включает в себя следующие этапы работы:
По аналитическому выражению различают следующие виды трендов: ЛИНЕЙНЫЙ - ŷ = a + bt Величина параметра определяется с помощью МНК, который реализован в функции EXCEL «ЛИНЕЙН». Линейный тип тренда подходит для отображения тенденции примерно равномерного измерения уровней, т. е равными абсолютным приростом. Абсолютный прирост вычисляется со второй строчки и равен разнице между данным и предыдущим значением уровня ряда. Основные свойства линейного тренда: Равные изменения за равные промежутки времени. Если средний абсолютный прирост - положительная величина. то величина относительного прироста постепенно уменьшается. Если среднее абсолютное изменение – отрицательная величина, то относительное изменение увеличивается. ГИПЕРБОЛИЧЕСКИЙ – ŷ = a + b/T Содержание параметров гиперболы: а – предел, к которому стремится уровень ряда; b – основной параметр гиперболы: Если b больше 0, то уровень ряда снижается и стремится к а; Если b меньше 0, то уровень ряда замедленно возрастают и тоже стремятся к а. ПАРАБОЛИЧЕСКИЙ – ŷ = a + bt + ct2 Когда приросты абсолютных приростов примерно одинаковы, тогда применяют параболический тренд(вторые разницы примерно одинаковы) СТЕПЕННОЙ – ŷ = a * tb ПОКАЗАТЕЛЬНЫЙ – ŷ = a * bt Показательный тренд выбирается, когда РД характеризуется стабильными коэффициентами роста. |
29.Оценка параметров уравнения тренда временного ряда(ряда динамики - РД). Построение модели тенденции (уравнение тренда) включает в себя следующие этапы работы:
При исследовании полиномов разных степеней оценка производится с помощью МНК так же, как оценка параметров уравнения регрессии на основе пространственных данных. В качестве зависимой переменной рассматривается уровни динамического ряда У , а в качестве независимой фактор времени t, который обычно выражается рядом натуральных чисел 1,2,3,…n. Оценка параметров нелинейных по оцениваемым параметрам функции производится МНК после линеаризации, т.е приведении их к линейному виду. |
30.Оценка адекватности модели тенденции временного ряда(ряда динамики - РД). Коэффициент детерминации, средняя ошибка аппроксимации. Построение модели тенденции (уравнение тренда) включает в себя следующие этапы работы:
Модель тенденции считается адекватной реальному процессу, если теоретические (найденные по уравнению тренда) уровней ряда достаточно близко подходят к их фактическим значениям, т. е Уt и ŷt мало отличаются друг от i друга. Для оценки адекватности модели проводятся анализ остатков, т.е чем остатки больше, тем более адекватна модель. E(ипсилон)t = Yt- ŷt Модели тенденции можно сравнить по величине остаточной суммы квадратов. Чем меньше эта величина, тем в большей степени уравнение тренда подходит для описания тенденции другого ряда. К другим показателям при выборе функции тренда является коэффициент детерминации R2. Тем больше этот коэффициент, тем лучше данная модель описывает исходные данные в [0;1]. 1- R2 – отражает влияние случайной составляющей, т .е показывает какая доля вариации уровней РД не связана с тенденцией. Уравнение тренда хорошо описывает тенденцию, если отражает автокорреляцию в остатках, т.е остатки текущего периода момента времени не корреспондируют с остатками предыдущего периода или момента времени. Измерить автокорреляцию в остатках можно с помощью линейного коэффициента корреляции.(КОРРЕЛ) Качество полученного уравнения регрессии оценивают также с помощью средней относительной ошибки аппроксимации: А = 1/n*Σ│(yi - ŷi)/yi│*100% Допустимый предел:8-10%
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
31. Понятие и виды систем эконометрических уравнений. В виду многогранности экономические процессы наиболее полно могут быть описаны с помощью системы экономических уравнений, которые подразделяются на следующие виды:
Система независимых уравнений представляет собой систему , в которой эндогенные переменные (у1,у2,у3..) рассматриваются как функции объясняющих переменных (х1,х2...) Каждое уравнение такой системы является уравнением регрессии, нахождение параметров которого может быть осуществлено МНК, т.е каждое уравнение системы независимых уравнений рассматривается самостоятельно и в системе из п-уравнений п-раз применяется МНК. Пример системы независимых уравнений, содержащей 3 эндогенных переменных и 3 экзогенных переменных.
у1 = а1 + b11x1
+ b12x2
+ b13x3
+ e2(эпсилон-ошибка) y2 = a2 + b21x1 + b22x2 + b23x3+e2 у3 = a3 + b31x1 + b32x2 + b33x3 + e3 Cистема рекурсивных уравнений представляет собой системы, в которых эндогенные переменные У одного уравнения системы в каждом последующем уравнении является фактором на ряду с другими факторами. Пример:
y1 = a1 +
b11x1 + b12x2 + b13x3 + e1 y2 = a2 + c21y1 + b22x2 + e2 y3 = a3 + c31y1 + c32y2 + b34x4 + e3 Cистемы одновременных уравнений (взаимозависимых) представляет собой систему, в которой результативный признак одного уравнения системы входит во все другие уравнения системы в качестве фактора наряду с другими функциями. Пример:
y1 = a1
+ c12y2 + b11x1 + e1 y2 = a2 + c21y1 + c23y3 + b23x3 + e2 y3 = a3 + c23y2 + b23x3 + e3
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
30. |
29. |
28. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
31. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|


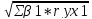
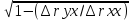
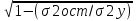 =
=
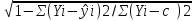
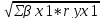
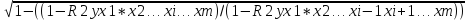
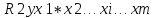 – множественный
коэффициент детерминации всего
комплекса m
факторов с результатом.
– множественный
коэффициент детерминации всего
комплекса m
факторов с результатом.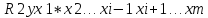 –тот же показатель
детерминации, но без введения в модель
фактора xi.
–тот же показатель
детерминации, но без введения в модель
фактора xi.