002. ЛЕКЦИИ 1-6 (ОПУТ) (МТП) (курсант) / Лекции / лекция 4 / лекция 4

Симплексный метод для решения ОЗЛП

Среди универсальных методов решения задач линейного программирования наиболее распространен симплексный метод (или симплекс-метод), разработанный американским ученым (Джордж Данциг).

Симплексный метод решения задач линейного программирования – это вычислительная процедура, основанная на принципе последовательного улучшения решений — перехода от одной базисной точки к другой, для которой значение целевой функции больше (эти операции фиксируются в симплексной таблице).

Доказано, что если оптимальное решение существует, то оно обязательно будет найдено через конечное число шагов (за исключением так называемой вырожденной задачи, при которой возможно явление “зацикливания”, т. е. многократного возврата к одному и тому же положению). Название метод получил от термина “n-мерный симплекс”. Геометрическая интерпретация метода состоит в последовательном движении по вершинам симплекса.

Процедура симплекс-метода содержит три существенных элемента:

1. указывается способ нахождения опорного плана или устанавливается невозможность его построения;

2. устанавливается признак, дающий возможность проверить, является ли план оптимальным;

3. устанавливается правило, по которому неоптимальный план можно улучшить.

Совокупность значений основных переменных x₁,x₂,…x_n, соответствующих какой-нибудь вершине многогранника ограничений называется опорным планом задачи.

Совокупность значений основных переменных x₁,x₂,…x_n и дополнительных переменных y₁,y₂,…y_m, соответствующих какой-нибудь вершине многогранника ограничений – называется опорным решением задачи.

Если в данной вершине достигается оптимум целевой функции, то опорный план и опорное решение называются соответственно оптимальным планом и оптимальным решением.

Из алгебраической характеристики вершины многогранника ограничений вытекает, что все n+m чисел, составляющих опорное решение, должны быть неотрицательными и притом не менее чем n из этих чисел должны быть равны нулю.

Вычисления по симплекс-методу организуются в виде симплекс-таблиц (см. табл. 1), которые являются сокращенной записью задачи линейного программирования в канонической форме. Перед составлением симплекс-таблицы задача должна быть преобразована, система ограничений приведена к допустимому базисному виду, c помощью которого из целевой функции должны быть исключены базисные переменные.

Таблица 1

Симплекс-таблица

БП (базисные переменные)	-x1	…	-xj	…	-xn	1 (столбец свободных членов, заключительный столбец)
y1	a11	…	a1j	…	a1n	b1
…	…	…	…	…	…	…
yi	ai1	…	aij	…	ain	bi
…	…	…	…	…	…	…
ym	ami	…	amj	…	amn	bm
z	-c1	…	-cj	…	-cn

Теорема 1. Признак опорности решения задачи.

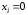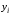Если на каком то шаге пересчета симплекс таблицы оказалось, что все элементы заключительного столбца неотрицательны (), то, полагая верхние переменные равными нулю (), а боковые переменные () равными соответствующим элементам заключительного столбца, получим некоторое опорное решение.

Теорема 2. Признак оптимальности решения.

Опорный план является оптимальным, если все элементы заключительной строки положительные, т.е. 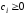, если задача на максимум, если на минимум то .

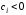В случае если это условие не выполняется, план нужно улучшить, т.е. сделать пересчет симплекс-таблицы по правилу:

1. в качестве разрешающего выбираем столбец, в котором нарушено условие неотрицательности (для задачи на максимум) или отрицательности (для задачи на минимум). Если таких столбцов несколько, разрешающий будет тот, которому соответствует наибольшее по модулю значение элемента заключительной строки, т.е. .

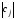2. далее определяют отношение элементов заключительного столбца 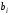к ненулевым элементам разрешающего столбца, взятых с одинаковыми знаками. Строку, в которой это отношение 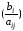минимальное, принимают за разрешающую строку. На пересечении разрешающей строки и разрешающего столбца будет находиться ведущий (разрешающий) элемент.

3. в дальнейшем базисная переменная, отвечающая строке разрешающего элемента, должна быть переведена в разряд свободных, а свободная переменная, отвечающая столбцу разрешающего элемента, вводится в число базисных. Строится новая таблица, содержащая новые названия базисных переменных: ведущий (разрешающий) элемент заменяется на обратное число с тем же знаком, элементы ведущей строки делятся на ведущий элемент, элементы ведущего столбца делятся на ведущий элемент и меняют свой знак.

4. В остальные клетки новой таблицы записывается результат преобразования элементов старой таблицы по правилу прямоугольника:

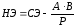
где: НЭ – новый элемент;

СЭ – старый элемент;

А – элемент ключевого столбца ключевых строк

В - элемент ключевой строки ключевого столбца

Р – разрешающий элемент

5. если после пересчета симплекс таблица вновь имеет место невыполнения условий оптимальности, то тогда таблицу пересчитывают по вышеприведенному правилу до тех пор, пока не получится оптимальное решение.

Пример: найти максимум функции 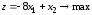, при ограничениях:

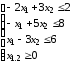
Для решения введем дополнительные переменные y₁, y₂, y₃ и перепишем ограничения в виде:

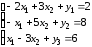
Выразим y₁, y₂, y₃ получим:

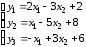
Составим симплекс-таблицу:

Таблица 4.2

БП	-x1	-x2	1
y1	-2	3	2	2/3=0,66 min
y2	-1	5	8	8/5=1,6
y3	1	-3	6
z	8	-1	0

В качестве разрешающего выбираем столбец (из строки z), в котором нарушено условие неотрицательности (т.к. задача на максимум), в данном случае это “-1”, x₂ – ведущий столбец.

Справа от таблицы 4.2 записаны отношения элементов заключительного столбца к элементам ведущего столбца взятых с одинаковыми знаками, выбираем из этого отношения минимальное и получаем ведущую строку. На пересечении ведущего столбца и ведущей строки будит находиться ведущий элемент (в таблице он выделен).

Далее базисная переменная, отвечающая строке разрешающего элемента (y₁), должна быть переведена в разряд свободных, а свободная переменная, отвечающая столбцу разрешающего элемента (x₂), вводится в число базисных. Строится новая таблица 4.3, содержащая новые названия базисных переменных: ведущий (разрешающий) элемент (т.е. 3) заменяется на обратное число с тем же знаком (1/3), элементы ведущей строки делятся на ведущий элемент (3), элементы ведущего столбца делятся на ведущий элемент (3) и меняют свой знак.

В остальные клетки новой таблицы записывается результат преобразования элементов старой таблицы по правилу прямоугольника, например: 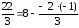и т.п.

Таблица 4.3

БП	-x1	-y1	1
x2	-2/3	1/3	2/3
y2	7/3	-5/3	14/3
y3	-1	1	8
z	22/3	1/3	2/3

Т.к. все элементы заключительной строки (см. табл. 4.3) оказались положительными, то мы достигли максимума. Оптимальное решение содержится в заключительном столбце, а именно:

x₂=2/3, y₂=14/3, y₃=8

Остальные переменные все равны нулю:

x₁=y₁=0

Таким образом, оптимальный план будет:

x₁=0; x₂=2/3; y₁=0; y₂=14/3; y₃=8.

Оптимальное значение максимизируемой функции Z_max=2/3

Рекомендуется всякий раз при переходе к новой таблице, прежде всего, заполнить заключительную строку, т.к. если окажется, что все ее элементы уже удовлетворяют условию оптимальности, то нет необходимости вычислять другие элементы, кроме элементов заключительного столбца.