002. ЛЕКЦИИ 1-6 (ОПУТ) (МТП) (курсант) / Лекции / лекция 3 / лекция 3

общая задача линейного программирования (озлп) и методы ее решения

1. Постановка и математическая модель ОЗЛП

Пусть некоторое предприятие выпускает n видов продукции. При изготовлении этой продукции предприятие использует m видов ресурсов, объемы которых заданы в количествах b₁, b₂…b_m. Также заданы расходы (a_ij) i-го вида ресурсов (i=1…m) на производство единицы продукции j-го вида (j=1…n). Кроме того известна стоимость единицы продукции - c_ij.

Необходимо определить объем производства продукции, при котором достигается максимальный доход от реализации, при условии, что вся продукция найдет сбыт.

Для решения задачи, обозначим x_j – количество продукции j-то вида, которое необходимо произвести в планируемом периоде.

Известно, что доход данного предприятия складывается как сумма произведение объема выпущенной продукции, (при условии, что она найдет сбыт), и стоимости единицы данной продукции (т.е. )

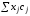Тогда целевая функция примет вид:

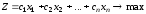или

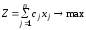
При этом расходы ресурсов на производство продукции a_ij не должны превышать запасы ресурсов на производство b₁, b₂…b_m,, т.е. что бы удовлетворялись неравенства:

или

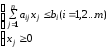
Значения x₁, x₂…x_n должны быть неотрицательными, т.к. количество продукции не может быть отрицательным.

Целевая функция и система ограничений составляют математическую модель линейного программирования.

При неравенствах вида: 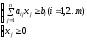, как правило формулируется задача на минимум, т.е. целевая функция имеет вид:

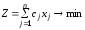
При нарушении данного соответствия неравенство приводят к нужному виду, изменив знаки при a_ij и b_i на противоположные.

2. Геометрическая интерпретация ОЗЛП и графический способ ее решения

Задачу линейного программирования и численный метод ее решения можно истолковать геометрически. Геометрическое изображение дает ясное представление о ходе решения задачи линейного программирования и приводит к простому графическому способу решения для того случая, когда число неизвестных параметров управления сводится к двум.

Приступая к изложению геометрической интерпретации, прежде всего, необходимо изучить три составляющих, из которых состоит задача линейного программирования: 1) целевую функцию; 2) систему линейных ограничений; 3) требование неотрицательности искомых параметров. С этой целью будим рассматривать геометрические образы, возникающие на координатной плоскости двух переменных. Обычно в этом случае оси координат обозначают буквами x и y, но, имея в виду дальнейшее обобщение на многомерные пространства, будем обозначать оси координат буквами x₁ и x₂.

Пусть дана задача линейного программирования (например, на максимум):

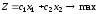, (4.1)

при ограничениях:

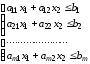(4.2)

и при требовании неотрицательности переменных:

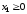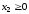, (4.3)

Рассмотрим систему ограничений 4.2 и изобразим ее на плоскости. Данная система ограничений изображается на плоскости некоторой многоугольной областью, которая представляет собой замкнутый многоугольник. Данная многоугольная область всегда является выпуклой, т.е. такой, которая вместе с любыми двумя точками содержит и весь отрезок, их соединяющий (рис. 4.1), а не такой, какая изображена на рисунке 4.2.

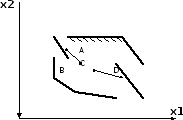
Рис. 4.1.

Рис. 4.2.

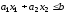
Каждое линейное неравенство системы 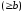можно изобразить на плоскости Ox₁x₂ некоторой полуплоскостью, которую можно найти, построив прямую и подставив в левую часть ее уравнения координаты какой-нибудь точки, не лежащей на этой прямой.

Важно отметить, что система неравенств: 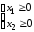, выражающих требование неотрицательности параметров задачи линейного программирования, изображается первым квадрантом координатной плоскости Ox₁x₂.

После изображения на плоскости системы ограничений, проведем какую-нибудь определенную линию уровня Z=const целевой функции, например прямую 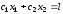, и покажем стрелками, куда ее надо двигать, чтобы целевая функция увеличивалась (см. рис. 4.3).

Рис. 4.3.

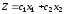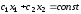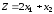Для того, что бы узнать в каком направлении надо передвигать прямую (l), достаточно зафиксировать значение константы в уравнении Z=const. Тогда получится какая то определенная прямая (l), и, чтобы ответить на поставленный вопрос, достаточно узнать с какой стороны от прямой (l), целевой функции больше фиксированной константы, поставленной в правую часть уравнения . Например, целевая функция увеличивается при движении, показанном на рисунке 4.4 стрелками около прямой . На том же рисунке показано, в какую сторону увеличивается целевая функция .

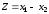Рис. 4.4.

Очевидно, что мы найдем искомый оптимум, когда прямая (l), двигаясь к границе многоугольника ограничений, покинет этот многоугольник – это произойдет в некоторой вершине многоугольника ограничений. Определив координаты x_1B и x_2B вершины B, найдем оптимальный план: x_1опт=x_1B и x_2опт=x_2B. Вычислив затем значение целевой функции в вершине B, найдем искомый оптимум:

Если бы при тех же ограничениях была поставлена задача на минимум, то линию уровня целевой функции – прямую (l) – надо двигать в противоположную сторону, и мы получим минимум снова в некоторой вершине C многоугольника ограничений.

Если область, задаваемая ограничениями, бесконечна (см. рис. 4.5), то один из оптимумов (максимум или минимум) может стать бесконечным, но другой по-прежнему достигается в некоторой вершине.

Рис. 4.5.

Может случиться, что линия уровня целевой функции – прямая (l) – окажется параллельной какому то звену многоугольника ограничений (см. рис. 4.6).

Рис. 4.6.

В этом случае (при отыскании одного из оптимумов) прямая (l), покидая многоугольник ограничений, ляжет на параллельное ей звено и координаты любой точки этого звена дадут оптимальный план, в этом случае имеем альтернативные оптимальные планы.

Пример: Найти максимум функции z=2x₁+3x₂ при ограничениях:

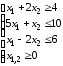
Для решения построим прямые и определим общую часть полуплоскостей, изображающих неравенства – ограничения задачи.

l₁: x₁+2x₂=4

x1	0	4
x2	2	0

l₂: 5x₁+x₂=10

x1	0	2
x2	10	0

l₃: x₁-2x₂=6

x1	0	6
x2	-3	0

Построим линию уровня целевой функции z=2x₁+3x₂, и узнаем, в какую сторону ее надо параллельно перемещать, чтобы целевая функция увеличивалась (см. рис. 4.7).

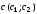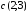Вектор целевой функции имеет вид: , в данном случае . Уравнение целевой функции:

2x₁+3x₂=0

x₁=0, x₂=0

x₁=1, x₂=-2/3

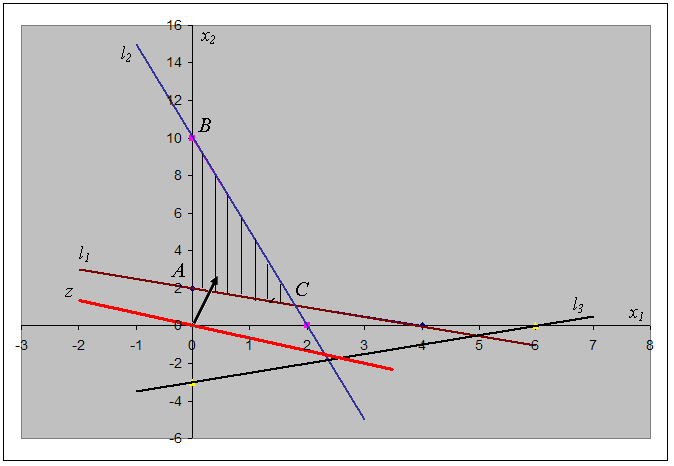
Рис. 4.7

Из рисунка 4.7 видно, что максимальное значение функция z достигает в вершине точки B (пересечения прямой l₂ с осью x₂), для нахождения координат точки B необходимо решить систему уравнений:

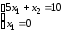
Имеем:

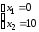
Следовательно, z_max=2·0+3·10=30.

Пример: Найти максимум функции z=2x₁+3x₂ при ограничениях:

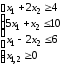
Для решения построим прямые и определим общую часть полуплоскостей, изображающих неравенства – ограничения задачи.

l₁: x₁+2x₂=4

x1	0	4
x2	2	0

l₂: 5x₁+x₂=10

x1	0	2
x2	10	0

l₃: x₁-2x₂=6

x1	0	6
x2	-3	0

Построим линию уровня целевой функции z=2x₁+3x₂, и узнаем, в какую сторону ее надо параллельно перемещать, чтобы целевая функция увеличивалась (см. рис. 4.7).

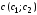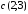Вектор целевой функции имеет вид: , в данном случае . Уравнение целевой функции:

2x₁+3x₂=0

x₁=0, x₂=0

x₁=1, x₂=-2/3

Рис. 4.7

Из рисунка 4.7 видно, что максимальное значение функция z достигает в вершине точки B (пересечения прямой l₂ с осью x₂), для нахождения координат точки B необходимо решить систему уравнений:

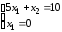
Имеем:

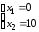
Следовательно, z_max=2·0+3·10=30.