Мат. логика все лекции / Lekcija_2

Лекция 2 Булевы функции и их обобщение

Понятие булевой функции

Определение 2.1. Функция f, зависящая от n переменных x₁, x₂, ...., x_n, называется булевой, или переключательной, если функция f и любой из ее аргументов х_i, (i  1..n) принимают значения только из множества {0, 1}. Аргументы булевой функции также называются булевыми.

Произвольная булева функция задается одним из трех способов: матричным (табличным), геометрическим и аналитическим.

При матричном способе булева функция f (х₁, ...,х_n) задается таблицей истинности (табл. 2.1 и 2.2), в ее левой части представлены все возможные двоичные наборы длины n, а в правой – значения функции на этих наборах.

Таблица 2.1			Таблица 2.2
х1х2х3			Номер набора
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1	0 1 0 0 1 1 0 1		0 1 2 3 4 5 6 7	0 1 0 0 1 1 0 1

Под двоичным набором y = <y₁, y₂,...,y_n> yi  {0, 1} понимается совокупность значений аргументов х₁, х₂, ..., x_n булевой функции f. Двоичный набор имеет длину n, если он представлен n цифрами из множества {0,1}. В табл. 1.1 представлены все двоичные наборы длины 3.

Иногда двоичные наборы в таблице истинности булевой функции удобно представлять номерами наборов. Запишем аргументы х₁, х₂, ..., x_n в порядке возрастания их индексов. Тогда любой двоичный набор y = <y₁, y₂,...,y_n> y_i  {0, 1} можно рассматривать как целое двоичное число N:

N=y₁*2^n-1+y₂*2^n-2+...+y_n,

называемое номером набора y. Например, двоичные наборы 101 и 111 имеют номера 5 и 7 соответственно. Очевидно, любая булева функция может быть задана таблицей истинности, в которой двоичные наборы заменены своими номерами (табл. 2.2).

Булевы функции, зависящие от большого числа переменных, задавать таблицей истинности неудобно в силу ее громоздкости. Например, таблица истинности булевой функции 8 переменных будет содержать 2⁸ = 256 строк. Поэтому для задания функций многих переменных удобно использовать модификацию таблицы истинности.

Рассмотрим способ построения такой таблицы истинности для функции n переменных. Множество из n переменных функции разбивается на два подмножества: х₁, х₂, ..., х_j-1 и х_j, х_j+1, ..., х_n. Переменными x₁, x₂, ..., x_n отмечают строки таблицы истинности, задавая в каждой строке значение соответствующего двоичного набора длины j-1. Переменными x_j, x_j+i, ..., x_n отмечают ее столбцы, задавая в каждом столбце значения соответствующего двоичного набора длины n-j+1. Значение функции записывается в клетке на пересечении соответствующей строки и столбца (табл. 2.3).

Таблица 2.3

x1,x2,...xj-1	xj, xj+1, ...,xn
	00...0	0...1	...	11...1
00...0			...
00...1			...
...	...	...	...	...
11...1			...

Пример 2.1. Построить таблицу истинности для функции четырех переменных f (х₁, x₂, x₃, х₄) = (х₁ Ú x₂ Ú x₃ Ú х₄) Ù¬х₁

x1, x2,	x3, x4
	00	01	10	11
00	0	1	1	1
01	1	1	1	1
10	0	0	0	0
11	0	0	0	0

При геометрическом способе булева функция f (х₁, ..., х_n) задается с помощью n-мерного куба. В геометрическом смысле каждый двоичный набор у = <y₁, y₂,...,y_n>, y_i  {0,1} есть n-мерный вектор, определяющий точку n-мерного пространства. Исходя из этого, все множество наборов, на которых определена функция n переменных, представляется вершинами n-мерного куба. Отмечая точками вершины куба, в которых функция принимает единичное (либо нулевое) значение, получим геометрическое представление функции. Например, булева функция, заданная табл. 2.1, геометрически представляется 3-мерным кубом (рис. 2.1).

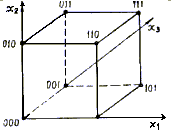
Рис. 2.1. Геометрическое представление булевой функции трех переменных.

При аналитическом способе булева функция задается формулами, т. е. аналитическими выражениями, построенными на основе операций булевой алгебры. Аналитический способ задания булевых функций занимает особое место в проектировании цифровых автоматов. Фактически, все преобразования над булевыми функциями, необходимые для построения цифровых автоматов, ведутся на аналитическом уровне.

Рассмотрим области определения булевых функций. Как уже отмечалось, между двоичными наборами и двоичными числами существует взаимно однозначное соответствие. Следовательно, существует 2ⁿ различных наборов двоичных переменных.

Таким образом, областью определения булевой функции n переменных при матричном способе задания является множество всех возможных двоичных наборов длины n, а при геометрическом способе задания – множество всех вершин n-мерного единичного куба.

Определение 2.2. Булеву функцию, определенную на всех своих наборах, называют полностью определенной.

В табл. 2.1, 2.2 приведены примеры полностью определенных булевых функций.

Определение 2.3. Булеву функцию n переменных называют неполностью определенной или частичной, если она определена не на всех двоичных наборах длины n. Неполностью определенная булева функция не попадает под определение, данное в начале лекции, но при произвольном доопределении (на всех наборах, на которых она не определена) это несоответствие снимается.

Легко убедиться, что если булева функция f не определена на m наборах аргументов, то путем ее доопределения можно получить 2^m различных полностью определенных функций. В табл. 2.4 приведен пример неполностью определенной булевой функции трех переменных.

Таблица 2.4

х1х2х3	F
000 001 010 011 100 101 110 111	0 1 - 0 1 - 1 -

Существует не более чем 2^{2^n} различных булевых функций n переменных. К этому выводу легко прийти, пользуясь простыми комбинаторными рассуждениями, и вспомнив, что на каждом из 2ⁿ наборов функции могут принимать два значения.

Наиболее часто употребляются следующие функции двух переменных, представленные в табл. 2.5.

Таблица 2.5

х1х2	f0	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
00 01 10 11	0 0 0 0	0 0 0 1	0 0 1 0	0 0 1 1	0 1 0 0	0 1 0 1	0 1 1 0	0 1 1 1	1 0 0 0	1 0 0 1	1 0 1 0	1 0 1 1	1 1 0 0	1 1 0 1	1 1 1 0	1 1 1 1

f ₀ (x₁, x₂) = 0 – тождественный ноль (константа 0);

f ₁ (x₁, x₂) = x₁  x₂ – конъюнкция (логическое И);

f ₃ (x₁, x₂) = x₁ – повторение x₁;

f ₅ (x₁, x₂) = x₂ – повторение x₂;

f ₆ (x₁, x₂) = x₁  x₂ – сложение по модулю 2 или сумма mod 2;

f ₇ (x₁, x₂) = x₁  x₂ – дизъюнкция (логическое ИЛИ);

f ₈ (x₁, x₂) = x₁ | x₂ – функция Вебба (стрелка Пирса);

f ₉ (x₁, x₂) = x₁ ~ x₂ – эквивалентность;

f ₁₃(x₁, x₂) = x₁  x₂ – импликация;

f ₁₄(x₁, x₂) = x₁\ x₂ – штрих Шеффера;

f₁₅(x₁, x₂) = 1-тождественная единица (константа 1).

Рассмотренные простейшие булевы функции позволяют строить новые булевы функции с помощью обобщенной операции, называемой операцией суперпозиции. Фактически операция суперпозиции заключается в подстановке вместо аргументов других булевых функций (в частности аргументов). Например, из функции f ₁ (x₁, x₂) с помощью подстановки f₃ (х₄, x₈), f₂ = x₃ вместо аргументов х₁ и х₂ соответственно получаем функцию f₁ (f₃ (x₄, x₈), x₃). Последняя от переменных х₁, и х₂ уже не зависит.

Отметим, что реально элементарной функции соответствует реализующий ее элемент, а суперпозиции булевых функций соответствует соединение элементов.

Операция суперпозиции позволяет увидеть качественный переход от n = 1 к n = 2. Действительно, суперпозиция функций одного аргумента порождает функции одного аргумента. Суперпозиция функций двух аргументов дает возможность строить функции любого числа аргументов (в приведенном примере построена функция трех переменных).

Суперпозиция булевых функций представляется в виде логических формул. Однако следует отметить:

• одна и та же функция может быть представлена разными формулами;

• каждой формуле соответствует своя суперпозиция и, следовательно, своя схема соединений элементов;

• между формулами представления булевых функций и схемами, их реализующими, существует взаимооднозначное соответствие.

Очевидно, среди схем, реализующих данную функцию, есть наиболее простая. Поиск логической формулы, соответствующей этой схеме, представляет большой практический интерес, а преобразование формул булевых функций основано на использовании соотношений булевой алгебры.

Преобразование формул булевых функций применением только аксиом булевой алгебры малоэффективно. Для упрощения формул используется целый ряд соотношений.

Минимизация булевых функций

При проектировании цифровых схем широко используются методы минимизации булевых функций, позволяющие получать рекомендации для построения экономичных схем. Общая задача минимизации булевых функций может быть сформулирована следующим образом: найти аналитическое выражение заданной булевой функции в форме, содержащей минимально возможное число букв. Следует отметить, что в общей постановке данная задача пока не решена, однако достаточно хорошо исследована в классе дизъюнктивно-конъюнктивных форм.

Определение 2.4. Элементарной конъюнкцией называется конъюнкция конечного числа различных между собой булевых переменных, каждая из которых может иметь или не иметь отрицания.

Определение 2.5. Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция элементарных конъюнкций.

Определение 2.6. Элементарной дизъюнкцией называется дизъюнкция конечного числа различных между собой булевых переменных, каждая из которых может иметь или не иметь отрицания.

Определение 2.7. Конъюнктивной нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций.

Совершенные нормальные формы

Определение 2.8. Совершенной дизъюнктивной нормальной формой (СДНФ) формулы А называется ДНФ А, обладающая свойствами совершенства:

1) каждая элементарная конъюнкция формулы содержит все переменные, входящие в формулу А;

2) все элементарные конъюнкции формулы различны;

3) ни одна элементарная конъюнкция формулы не содержит одновременно переменную и ее отрицание;

4) ни одна элементарная конъюнкция формулы не содержит одну и ту же переменную дважды.

СДНФ можно получить двумя способами: 1) с помощью таблицы истинности; 2) с помощью равносильных преобразований.

С помощью таблицы истинности, определяющей формулу А, СДНФ А строится следующим образом:

– для каждого набора переменных, на которых функция принимает значение 1, запишем конъюнкцию элементарных переменных высказываний, взяв за член конъюнкции х_i, если ее значение на указанном наборе значений переменных равно 1, и взяв за член конъюнкции отрицание х_i, если ее значение на указанном наборе – 0;

– запишем дизъюнкцию всех полученных таким образом элементарных конъюнкций.

Правило получения СДНФ А с помощью равносильных преобразований:

– для формулы А получить любую ДНФ;

– из ДНФ А путем равносильных преобразований получаем СДНФ:

• пусть В – элементарная конъюнкция ДНФ, не содержащая х_i, тогда заменяем элементарную конъюнкцию В на элементарную конъюнкцию ;

• если в ДНФ встретятся две одинаковых элементарных конъюнкции, то лишнюю можно отбросить, т.к. ;

• если в некоторую элементарную конъюнкцию В переменная х_i входит дважды, то лишнюю переменную надо отбросить, т.к. х_i Ù х_i = х_i;

• если элементарная конъюнкция в ДНФ содержит конъюнкцию переменной х_i и ее отрицания, то эту конъюнкцию нужно отбросить, так как она равна нулю, и на значение дизъюнкции не влияет.

Определение 2.9. Совершенной конъюнктивной нормальной формой (СКНФ) формулы А называется КНФ А, обладающая четырьмя свойствами:

1) каждая элементарная дизъюнкция, входящая в КНФ А, содержит все переменные, входящие в формулу А;

2) все элементарные дизъюнкции различны;

3) каждая элементарная дизъюнкция, входящая в КНФ А, содержит переменную один раз;

4) ни одна элементарная дизъюнкция не содержит одну и ту же переменную и ее отрицание.

СКНФ можно получить двумя способами: 1) с помощью таблицы истинности; 2) с помощью равносильных преобразований.

С помощью таблицы истинности, определяющей формулу А, СКНФ А строится следующим образом:

– для каждого набора переменных, на которых функция принимает значение 0, запишем дизъюнкцию элементарных переменных высказываний, взяв за член дизъюнкции х_i, если ее значение на указанном наборе значений переменных равно 0, и взяв за член дизъюнкции отрицание х_i, если ее значение на указанном наборе – 1;

– запишем конъюнкцию всех полученных таким образом дизъюнкций.

Иначе данное правило можно записать так .

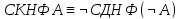Правило получения СКНФ А с помощью равносильных преобразований:

– для формулы А получить любую КНФ;

– из КНФ А путем равносильных преобразований получаем СКНФ:

• пусть В – слагаемое КНФ, не содержащее х_i, тогда заменяем слагаемое В на слагаемое ;

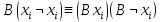• если в некоторую элементарную дизъюнкцию В переменная х_i входит дважды, то лишнюю переменную надо отбросить, т.к. х_i  х_i = х_i;

• если в КНФ встретятся две одинаковых элементарных дизъюнкции, то лишнюю можно отбросить, т.к. ВÙB=B;

• если элементарная дизъюнкция в КНФ содержит переменную х_i и ее отрицания, то ее нужно отбросить, так как она равна 1, и на значение конъюнкции не влияет.

Теорема 2.1. Для того чтобы формула алгебры логики была тождественно истинной (ложной), необходимо и достаточно, чтобы любая элементарная дизъюнкция (конъюнкция), входящая в КНФ А (ДНФ А), содержала переменную и ее отрицание.