Лекция 9 Сложность алгоритмов и вычислений

Вычислительные задачи должны решаться за приемлемое время с использованием ограниченных ресурсов памяти. Это приводит к понятию временной и пространственной сложности алгоритма. Как правило, алгоритм включает в себя различные операции, которые могут требовать разного времени для своего выполнения. Например, перемножая две вещественные матрицы, мы выполняем операции сложения и умножения вещественных чисел. В предельном случае, можно считать, что для умножения двух чисел нужна единица времени, а сложение выполняется мгновенно.

В этом случае, время, затрачиваемое алгоритмом на решение задачи, равняется числу выполняемых операций умножения. Получается так называемая мультипликативная сложность алгоритма. С другой стороны, можно считать, что время, затрачиваемое на выполнение сложения двух чисел, примерно такое же, что и время, затрачиваемое на их умножение. В этом случае, для определения сложности алгоритма нам нужно подсчитать общее количество операций сложения и умножения. Получаем полную арифметическую сложность алгоритма. Можно, конечно, рассмотреть и случай, когда подсчитываются только операции сложения, пренебрегая операциями умножения. Получаем аддитивную сложность.

В других алгоритмах операции могут быть другими, так же как и соотношения времен их выполнения. Например, во многих алгоритмах сортировки, ключевую роль играют операции сравнения двух элементов и операции перестановки двух элементов. В зависимости от типа элементов, соотношение времен выполнения этих операций может быть разное.

Для решения одной и той же задачи могут существовать разные алгоритмы. Например, для умножения вещественных матриц A=(a_ij) и В=(b_ij) размера 2×2 можно воспользоваться формулами AB=C, где c_ij=a_i1b_1j + a_i2b_2j (i,j=1,2). Для нахождения каждого из четырех элементов матрицы C мы выполняем две операции умножения и одну сложения. Получаем мультипликативную сложность 8 (и полную арифметическую сложность 12). Штрассен показал, что эта же задача может быть решена с использованием только 7 операций умножения (за счет увеличения числа сложений).

Под временной сложностью задачи мы понимаем минимальную временную сложность алгоритма, с помощью которого эта задача может быть решена. Таким образом, мультипликативная сложность умножения двух квадратных вещественных матриц второго порядка не превосходит 7. Можно доказать, что эта сложность равна 7, но этот результат гораздо менее тривиален. Как правило, оценить снизу сложность задачи много труднее, чем оценить ее сверху, поскольку для оценки сверху достаточно предъявить алгоритм, а для оценки снизу — доказать, что таких алгоритмов не существует.

Наряду с временной сложностью алгоритмы характеризуются пространственной сложностью. Для задач символьных вычислений характерно «разбухание» промежуточной информации: входные данные и окончательные результаты могут иметь компактную форму, но на промежуточных этапах вычислений требуется хранить большой объем информации. Минимальный размер памяти, достаточный для хранения данных, используемых алгоритмом, называется пространственной сложностью алгоритма. Пространственная сложность задачи определяется аналогично временной сложности, как минимальная пространственная сложность алгоритма, решающего данную задачу.

Как правило, на вход алгоритма могут подаваться разные данные. В частности, на вход алгоритма умножения двух вещественных матриц порядка 2 подаются 8 вещественных чисел (элементы перемножаемых матриц). В других случаях количество чисел, поступающих на вход алгоритма, может зависеть от некоторого параметра. Например, на вход алгоритма умножения двух вещественных квадратных матриц порядка п подаются 2n² вещественных чисел (элементы перемножаемых матриц). Естественно, что количество операций также будет зависеть от n. Так, для умножения двух квадратных матриц любого порядка n может быть применена формула

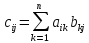(9.1)

Легко подсчитать, что при этот требуется n³ умножений и n³−n² сложений. Таким образом, мультипликативная сложность алгоритма равна n³, а полная арифметическая сложность равна 2n³−n². Здесь мы имеем дело с зависимостью сложности алгоритма от некоторого входного параметра (натурального числа n, равного порядку перемножаемых матриц).

Как правило, точно сосчитать число операций, выполняемых алгоритмом, довольно трудно, поэтому широко применяются верхние и нижние оценки временной сложности алгоритма. Для описания асимптотических оценок используются специальные обозначения.

Пусть T(x) и f(x) – две неотрицательные функции, определенные для любых положительных вещественных значений x. Мы будем писать

• T(x) = O(f(x)), если существуют константа C и значение x₀ такие, что T(x) ≤ Cf(x) для всех x ≥ х₀;

• T(x) = Ω(f(x)), если существуют константа C и значение x₀ такие, что T(x) ≥ C f(x) для всех x ≥ x₀;

• T(x) = Θ(f(x)) тогда и только тогда, когда T(x) = O(f(x)) и T(x)=Ω(f(x)).

Если функции f(x) и g(x) таковы, что f(x) = Θ(g(x)), то мы будем говорить, что они имеют одинаковый асимптотический рост.

В рассматриваемых ниже случаях, как правило, аргумент x будет натуральным числом (мы будем обычно обозначать его n), а функции T(n) и f(n) будут принимать только положительные значения. В таком случае условие «для всех x ≥ х₀» можно заменить на «для всех n>0».

Докажем, что для асимптотических оценок справедливы следующие правила:

1. если f(n) = O(g(n)) и g(n) = O(h(n)), то f(n) = O(h(n));

2. если f(n) = O(kg(n)) для некоторой константы k > 0, то f(n) = O(g(n));

3. если f₁(n) = O(g₁(n)) и f₂(n) = O(g₂(n)), то f₁(n) + f₂(n) = O(max(g₁(n), g₂(n)));

4. если f₁(n) = O(g₁(n)) и f₂(n) = O(g₂(n)), то f₁(n) ∙ f₂(n) = O(g₁(n) ∙g₂(n)).

В этих обозначениях мультипликативная сложность алгоритма умножения квадратных матриц порядка n по формуле (9.1) может быть описана как O(n³), или Ω(n³), или Θ(n³). Мультипликативную сложность задачи умножения двух квадратных матриц порядка n мы можем оценить только как O(n³), поскольку предъявлен алгоритм с такой мультипликативной сложностью, решающий эту задачу.

Оценка мультипликативной сложности задачи умножения квадратных матриц представляет собой весьма трудную задачу, над которой работали и продолжают работать многие известные математики. Предположим, что n = 2^k. Представим матрицы-сомножители как квадратные матрицы второго порядка, элементами которых являются матрицы порядка n/2 = 2^k−1. Перемножим эти матрицы по методу Штрассена (этот метод применим к матрицам с элементами из произвольного кольца, не обязательно даже коммутативного). Получим 7 произведений матриц порядка 2^k−1. Эти умножения также будем выполнять по методу Штрассена. Получим 7² произведений матриц порядка 2^k−2 и т.д. В итоге нам придется выполнить 7^k умножений вещественных чисел. Переходя к n, получаем

7^k ₌ 7^log₂ ⁿ ₌ 2^log₂ ^7∙log₂ ⁿ ₌ n^log₂ ⁷.

Очевидно, что log₂7<3=log₂8. Значит, оценка O(n^log₂⁷) является более сильной, чем O(n³), т.е. для любых положительных констант c₁ и c₂ существует натуральное n₀ = n₀(c₁,c₂) такое, что c₁n^log₂ ⁷ < c₂n³ при всех n > n₀.

Довольно просто показать, что ограничение n = 2^k не является существенным и выписанная асимптотическая оценка верна при любых достаточно больших n. Для перемножения по алгоритму Штрассена матриц, порядок n которых не является степенью двойки, т.е. 2^k < n < 2^k+1 для некоторого натурального k, достаточно дополнить перемножаемые матрицы единицами на главной диагонали до матриц размера 2^k+1. Легко видеть, что асимптотическая оценка сложности при этом остается верной.

Дальнейшие усилия математического сообщества привели к тому, что, применяя изощренные методы, показатель степени в оценке мультипликативной сложности умножения матриц удалось понизить до 2,39, т.е. имеем оценку O(n^2,39). Гораздо хуже обстоит дело с оценкой снизу. Удается только доказать, что она не ниже чем Ω(n²).

В качестве универсального параметра, зависимостью от которого можно характеризовать временную сложность алгоритма, рассмотрим размерность задачи.

Под размерностью задачи понимают количество информации, поступающей на вход алгоритма, решающего данную задачу. Элементарной единицей информации является бит, и всякая информация может быть закодирована некоторой последовательность битов. Предполагается, что на вход алгоритма подается конечная последовательность битов, длина которой и называется размерностью задачи или битовой длиной входа.

Например, размерность задачи перемножения двух квадратных вещественных матриц порядка n равна 2cn², где c – некоторая константа, определенная используемым представлением вещественных чисел (в частности, c = 32, если для записи вещественного числа отводится 4 байта). Для записи натурального числа n используется l = [log₂ n] битов, следовательно, размерностью задачи нахождения произведения ab двух натуральных чисел будет [log₂ a] + [log₂ b].

Оценим временную полную арифметическую сложность двух алгоритмов, решающих следующую задачу. Для натурального числа n найти сумму первых n натуральных чисел. Предполагаем, что n достаточно мало, так что любая арифметическая операция выполняется за единичное время.

Размерность задачи есть l = [log₂ п].

Сначала вычислим требуемую сумму по следующему алгоритму

S:= 0

для i от 1 до n

S :=S + i

Легко видеть, что количество операций оценивается как Θ(n) = Θ(2^l), т.е. зависимость временной сложности алгоритма от размерности задачи является экспоненциальной.

Для решения этой же задачи мы можем также применить формулу суммы арифметической прогрессии S = n(n+1)/2. При решении задачи по этой формуле количество операций не зависит от n и сложность оценивается как O(1).

В качестве второго примера рассмотрим нахождение суммы n чисел a₁,..., a_n. Предполагаем, что размерности машинного слова достаточно для представления любого из этих чисел (т.е.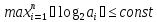не зависит отn) и любая арифметическая операция выполняется за единичное время.

В этом случае размерность задачи можно оценить

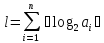
как Θ(n).

Используя алгоритм

S:= 0

для i от 1 до n

S := S + a_i,

мы получаем линейную зависимость Θ(l) временной сложности алгоритма от размерности задачи l.

Как правило, время работы алгоритма на различных входных данных одинаковой длины может существенно отличаться. Поэтому при оценке сверху асимптотической сложности алгоритма рассматривают сложность в худшем случае. Оценка сложности в худшем случае – это оценка, которая является истинной для любого допустимого набора входных данных заданной длины. Кроме того, часто используют оценку сложности алгоритма в среднем. Пусть входные данные длины l представляют собой множество допустимых наборов A_i. Предположим, что набор A_i подается на вход алгоритма с вероятностью p_i. Как обычно, полагаем, что 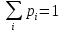. ПустьT_i – время работы алгоритма, если на его вход подан набор Ai. Тогда временн´ая сложность алгоритма в среднем определяется формулой.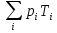

В качестве примера рассмотрим так называемую сиракузскую последовательность. Она строится индуктивно следующим образом. Пусть k – некоторое натуральное число. Полагаем a₀ = k. Далее, если a_i для некоторого i ≥ 0 определено, то а_i+1 вычисляется по следующим правилам:

• если a_i ≡ 0 (mod 3), то а_i+1 = a_i/3;

• если a_i ≡ 1 (mod 3), то а_i+1 = 2(a_i − 1)/3;

• если a_i ≡ 2 (mod 3), то а_i+1 = (13a_i − 2)/3.

Известная гипотеза состоит в том, что при любом начальном значении a₀=k сиракузская последовательность становится периодической, начиная с некоторого места (зависящего от k). Справедливость этой гипотезы проверена для достаточно больших k.

Рассмотрим алгоритм, на вход которого подается натуральное число к≤1000. Алгоритм последовательно вычисляет члены сиракузской последовательности и останавливается как только вновь вычисленное значение совпадает с каким-либо из предыдущих. Предполагаем, что для проверки, имеется ли какое-либо значение среди уже вычисленных членов последовательности, затрачивается нулевое время.

При написании программы можно воспользоваться фактом, что при сделанных предположениях (k ≤ 1000) сиракузская последовательность выходит на период, состоящий из небольших неотрицательных целых чисел (≤ 1000). Заведем массив с индексами от 0 до 1000 и заполним его значениями − 1. Вычислив очередной член t = a_i сиракузской последовательности, мы сравниваем t с числом 1000. Если t > 1000, то переходим к вычислению следующего члена последовательности. В противном случае, смотрим, что стоит в нашем массиве на t-ом месте. Если неотрицательное число v, то останавливаем вычисления, иначе меняем 1 на i и переходим к вычислению следующего члена последовательности.

Сиракузская последовательность представляет собой частный случай индуктивной последовательности. Последовательность {a₀, a₁,. .., a_n,...} называется индуктивной, если для любого i > 0 значение i-го члена полностью определяется значением (i-1)-го члена, т.е. существует функция f(x) такая, что a_i=f(a_i-1) для любого i > 0. Последовательность {а₀, а₁,..., a_n,...} называется периодической, если существуют неотрицательное целое M и натуральное T такие, что a_i = а_i+T для любого i ≥ M. Наименьшее такое M называется длиной нерегулярной части последовательности, а наименьшее такое T – длиной периода.

Предположим, что дана некоторая функция f, задающая периодическую индуктивную последовательность (в частности, f может быть отображением отрезка натурального ряда [0; N] в себя). Требуется найти длину нерегулярной части и периода этой последовательности.

Для решения задачи применим следующий метод. Храним в памяти вычисленную часть последовательности. Очередной член последовательности сравниваем с хранящимися в памяти и, если совпадения не обнаруживаем, добавляем его к имеющейся последовательности и вычисляем следующий член. Вычисления закончатся, когда мы обнаружим, что a_M+T=a_M.

При анализе сложности этого алгоритма мы сталкиваемся с ситуацией, когда оценить сложность алгоритма в терминах размерности задачи (длины входа) практически невозможно. Зато сложность может быть легко оценена в терминах суммы M+T. Для приложений таких оценок, как правило, достаточно. При оценке пространственной сложности алгоритма мы полагаем, что для хранения любого члена последовательности используется одна единица памяти. Нам нужно запомнить M+T элементов последовательности. Памятью, выделяемой для рабочих переменных, можно пренебречь. Таким образом, мы получаем оценку для пространственной сложности алгоритма Θ(M+T), где M – длина нерегулярной части, а T – длина периода последовательности. При оценке временной сложности алгоритма мы уже не можем пренебречь временем, затрачиваемым на проверку, встречается ли некоторый элемент в вычисленной части последовательности. Эта операция является «массовой», время ее выполнения пропорционально длине i вычисленной части последовательности. Пусть c₁ – время, затрачиваемое на сравнение текущего числа с любым их элементов запомненной последовательности. Для сравнения его со всеми элементами последовательности длины i требуется время c₁i. Суммируя по i от 1 до M+T, получаем 0,5c₁(М+Т)(М+Т-1). Это время, затраченное на все сравнения. Предположим, что время, затрачиваемое на вычисление очередного члена последовательности, не зависит от его номера и составляет c₂. Вычисление M+T членов займет c₂(М+Т) единиц времени. Выполнение всего алгоритма требует 0,5c₁(М+Т)(М+Т-1)+c₂(М+Т) единиц времени, что может быть оценено как ((M+T)²) при любом соотношении между c₁ и c₂.

Найдем алгоритм с временной сложностью O(M+T) и пространственной сложностью O(1), решающий эту задачу.

В компьютерной алгебре ключевую роль играют полиномиальные вычисления. При анализе алгоритмов работы с многочленами мы будем, как правило, рассматривать не зависимость временной или пространственной сложности алгоритмов от размерности задачи (длины входа), а зависимость таких параметров, как количество многочленов в промежуточных вычислениях, степени этих многочленов, их коэффициенты от соответствующих параметров входных данных и от количества переменных в кольце многочленов.

Наконец, в настоящее время все большее значение приобретают параллельные вычисления, когда для решения одной задачи используется несколько процессоров. Анализ параллельной сложности алгоритма подразумевает определение независимости различных операций в смысле возможности выполнения их одновременно на разных процессорах. В параллельных вычислениях используются различные архитектуры вычислительной системы и параллельная сложность может существенно зависеть от используемой архитектуры.

В заключение, оценим сложность арифметических операций над натуральными числами, выполняемых «столбиком». Пусть a и b – два натуральных числа, записанных в десятичной системе счисления, n = [lg a] +1 и m = [lg b] + 1 – количество десятичных цифр в записи чисел a и b. В качестве элементарных операций возьмем операции над одноразрядными числами, т.е. неотрицательными целыми числами, не превосходящими 9.

При сложении двух чисел выполняется max(n, m) элементарных сложений, учитывая наличие «переносов» (когда сумма двух однозначных чисел становится двузначным числом), количество операций может возрасти не более чем в два раза. Таким образом, мы получаем оценку арифметической сложности O(max(n, m)) = O(l), где l – размер входа.