
Савчук підручник
.pdfРозділ 3. Розв'язування геодезичних задач
Для знаходження невідомих s, A1, A2 використовують отримані вище формули для прямої геодезичної задачі. При цьому для
обчислення A , A достатньо знайти |
A |
|
|
1 |
(A A |
180o ) |
|||||||||||||||||||||||||
2 |
|||||||||||||||||||||||||||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
1 |
|
2 |
|
|
||||||||
та a A 180o A . Тоді отримаємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A A |
|
1 |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1 |
|
|
m |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
A A |
|
a 180o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
2 |
|
|
m |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Для знаходження Am представимо формули (3.60) та |
|||||||||||||||||||||||||||||||
(3.61) у виді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
scos A |
Q bM |
1 |
l2 sin2 |
Bm |
|
l2 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
m |
|
|
|
m |
|
24 |
|
|
|
12 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.64) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
ssin A |
P lN |
|
|
cosB |
|
|
|
|
1 |
l |
2 sin2 |
Bm |
|
|
b2 |
|
|
|
|||||||||||||
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
m |
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
24 |
|
|
|||||||||
Розділивши ці два рівняння, отримаємо |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
tgA |
|
P |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.65) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
m |
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Величину a знаходимо на основі формули (3.62) |
|
||||||||||||||||||||||||||||||
a lsin B |
|
1 |
l2 sin2 |
Bm |
|
b2 |
|
|
l2 |
. |
|
(3.66) |
|||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
m |
|
24 |
|
|
|
12 |
|
12 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Довжину геодезичної лінії sлегко знаходимо із рівнянь
(3.64)
132
Розділ 3. Розв'язування геодезичних задач
|
|
|
|
|
|
s Qcos A |
Psin A |
|
Q2 P2 . |
(3.67) |
|
m |
m |
|
|
|
|
3.6.2. Розв’язування прямої геодезичної задачі методом допоміжної точки (формули Шрейбера).
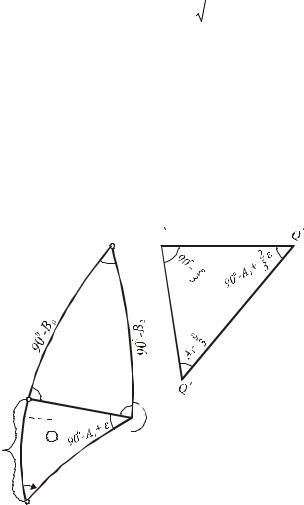
Нехай на рис.3.8 PQ1Q2 – сфероїдний полярний трикутник, який потрібно розвязати за такими даними: широтою B1 і довготою L1, довжиною s геодезичної лінії, що з'єднує точки Q1 i Q2, а також азимутом A1 цієї лінії в точці Q1 (прямий азимут).
а) б)
P |
C |
y |
2 |
l
C(B0=B1+b) 900
(d)
b(x)
A1
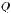 1(B1)
1(B1)
Розділимо
xs
1
y 900-a 

















 2(B2=B0-d)
2(B2=B0-d) 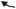 A2
A2
s
Рис. 3.8
трикутник PQ1Q2 (рис.3.8.а) на два
сфероїдних прямокутних трикутника геодезичною лінією Q2С, яка перпендикулярна меридіану PQ1 початкової точки. Широту
133
Розділ 3. Розв'язування геодезичних задач
точки С позначимо через Bo B1 b, а різницю широт
Bo B2 - через d.
Вивід формул Шрейбера буде складатись із наступних
етапів.
Із прямокутного сфероїдного трикутника Q1С Q2 за даними A1 і s визначають катети x і y, використовуючи теорему Лежандра та сферичний надлишок цього трикутника. На рис. 3.8.б представлений трикутник Q1’Q2’C’, який відповідає сфероїдному трикутнику Q1 С Q2.
Застосовуючи формули розкладу в ряд (3.32) можна розв’язати пряму геодезичну задачу для точок Q1 і С. Поскільки для цієї пари точок A1=0 і s=x, то все зводиться тільки до визначення різниці широт b.
За тими ж формулами розв’язують пряму геодезичну задачу з точки С , широта якої Bo B1 b тепер вже відома, на
точку Q2 , тобто при азимуті A1=90o та відстані s=y.
Отже, замість прямого застосування рядів (3.32) до точок Q1 і Q2 їх застосовують послідовно до точок Q1 і С , а потім до точок С і Q2, тобто у випадках, коли A=0o і A=90o.
В результаті |
отримаємо: |
B2 B1 |
b d |
та |
|
L2 L1 l. |
|
|
|
|
|
Сума всіх кутів навколо точки Q2 дасть |
|
|
|
||
A2 90o |
A1 |
90o |
a 360o , |
|
|
звідки |
|
|
|
|
|
A2 |
A1 |
180 a . |
|
(3.68) |
|
Розглянемо детальніше вивід основних формул. Із плоского трикутника Q1’С’Q2’, використовуючи теорему Лежандра, за формулою синусів отримаємо
134
|
Розділ 3. Розв'язування геодезичних задач |
|
|||||||
|
cos(A |
2 |
) |
|
sin(A |
) |
|
|
|
|
|
|
|
|
|||||
x s |
1 |
3 |
|
; |
y s |
1 |
3 |
, |
|
cos |
|
|
cos |
|
(3.69) |
||||
|
|
|
|
|
|
|
|||
|
3 |
|
|
|
|
3 |
|
|
|
де сферичний надлишок може бути достатньо точно обчислений за формулою
|
P |
|
1 |
|
1 |
|
xy |
|
s2 cos A sin A |
|
||
|
|
xycos |
|
|
|
1 1 |
. (3.70) |
|||||
R2 |
2 |
3 MN |
2MN |
2MN |
||||||||
|
|
|
|
|
|
|||||||
Для визначення широти Bo, використаємо першу формулу системи (3.32), в якій при підстановці похідних (до
третього порядку) врахуємо, що A 0o ,s x: |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
B |
B b B |
x |
|
|
3 |
x2 |
|
|
2tgB |
1 x3 |
|
|
2 (1 tg2B ).(3.71) |
||||||
|
|
|
|
|
|
|
|
|
|||||||||||
M |
|
|
|
|
2 M |
|
|
||||||||||||
o |
1 |
1 |
1 |
|
2 M |
N |
1 |
1 |
N 2 1 |
1 |
|||||||||
|
|
|
|
|
1 |
|
1 |
|
|
|
|
1 |
|
1 |
|
|
|||
|
|
Аналогічно поступають і при визначенні широти B2, |
|||||||||||||||||
тільки в цьому випадку вже A |
90o |
,s y: |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
B2 |
Bo |
1 |
|
|
y2 |
tgBo . |
|
|
(3.72) |
|||||||
|
|
|
2 Mo No |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Застосуємо тепер другу і третю формули системи (3.32) для визначення приростів довготи l та азимута a відповідно. При
цьому враховуємо, що Ao 90o ,s y:
135

Розділ 3. Розв'язування геодезичних задач
l |
|
|
|
y |
|
|
|
|
1 |
|
|
|
y3 |
|
|
tg2 Bo , |
|
|
|
|||
No |
cosBo |
|
|
|
|
No |
|
|
|
|
|
|
||||||||||
|
|
|
3 |
|
3 cosBo |
|
|
(3.73) |
||||||||||||||
|
|
y |
|
|
|
|
|
1 |
|
|
|
y3 |
|
|
|
|
|
|
||||
a |
|
|
tgB |
|
|
|
|
|
tgB |
|
(1 2tg2 B |
|
|
2 ). |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
No |
|
|
o |
|
|
|
6 No |
3 |
|
o |
|
|
o |
|
o |
|||||
Відповідно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L2 |
L1 |
l, |
A |
|
(3.74) |
A 180o a . |
||
2 |
1 |
|
3.6.3. Розв’язування головних геодезичних задач методом переходу на поверхню сфери (формули Бесселя).
Воснові способа Бесселя лежать умови:
1)геодезична лінія sміж точками Q1 і Q2 еліпсоїда (рис.3.9.а) зображується на сфері дугою великого кола між точками
Q1' і Q2' (рис.3.9.б);
2)у відповідних точках геодезичної лінії і дуги великого кола азимути рівні;
Еліпсоїд |
P |
Сфера |
||
l |
||||
|
|
|||
|
|
|
||
|
dl |
0u |
||
|
|
- |
2 |
|
|
|
|
||
|
|
0 |
|
|
|
|
9 |
|
|
P
|
|
|
|
|
|
|
|
|
|
|
- |
u |
1 |
|
0 |
9 |
0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
ds 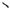 A1 m
A1 m 1(B1,L2)
1(B1,L2)

n
s
A2
2(B2 ,L2)
 A1 m
A1 m d n
d n
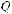 1
1
A2
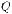 2
2
а) б)
Рис. 3.9
136
Розділ 3. Розв'язування геодезичних задач
3) широта будь-якої точки на сфері рівна приведеній широті відповідної точки на еліпсоїді, тобто сторони сферичного трикутника Q1' P' і Q2' P' відповідно рівні доповненням
до 900 приведених широт точок Q1 і Q2 на еліпсоїді.
Цими умовами забезпечується вище поставлена вимога однозначної відповідності між геодезичною лінією на еліпсоїді і дугою великого кола на сфері. Така відповідність називається ще бесселевим зображенням.
Залишається встановити зв’язки між різницею довгот l L2 L1 точок на еліпсоїді і аналогічною величиною - на
сфері; довжиною геодезичної лінії s на еліпсоїді і дугою великого кола на сфері. Хід отримання математичних формул цих зв’язків:
1.Вивід диференційних рівнянь, що встановлюють зв’язки між l і , s і .
2.Інтегрування отриманих диференційних рівнянь.
При наявності всіх необхідних зв’язків між відповідними величинами на еліпсоїді і сфері головні геодезичні задачі способом Бесселя розв’язуються за наступним планом:
а) перехід від елементів сфероїдного трикутника Q1PQ2 до елементів сферичного трикутника Q1' P'Q2' (рис. 3.9 а) і б));
б) розв’язування геодезичних задач (прямої чи оберненої) на сфері; с) перехід від обчислених елементів сферичного трикутника,
стосовно розв'язування прямої чи оберненої задачі, до відповідних елементів на еліпсоїді.
Вивід диференційних рівнянь Бесселя
Позначимо (рис. 3.9 ):
ds - нескінченно малий елемент mn геодезичної лінії sна еліпсоїді, якому відповідає елемент d m' n' в бесселевому зображенні на сфері; - азимут елемента ds ;
B і u - геодезична і приведена широти точки m; du і dl - різниці широт і довгот точок m і n; d - різниця довгот точок m' і n' на сфері.
137
Розділ 3. Розв'язування геодезичних задач
З цими позначеннями, прийнявши радіус одиницю, матимемо
du d cos MdB dscos ,
d cosu d sin N cosBdl dssin ,
звідки отримуємо
сфери за
(3.75)
(3.76)
|
du |
M |
d |
, |
|
(3.77) |
||
|
|
ds |
||||||
|
dB |
|
|
|
||||
N cosB dl |
|
ds |
. |
(3.78) |
||||
|
|
|
|
|
|
|||
cosu d |
|
|||||||
|
d |
|
||||||
На основі (2.19)
sinu |
|
|
1 e2 |
|
sinB |
|
, |
|
|
|
|
|
|
|
|||
1 e2 |
sin2 B |
|||||||
|
|
|
||||||
отримаємо
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosB |
|
|
|
|
e2 sin2 BcosB |
||||||||||
cosudu |
1 e |
2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dB. (3.79) |
|||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
3 |
|
|||||
|
|
|
|
(1 |
e |
2 |
sin |
2 |
B) |
|
|
|
(1 e |
2 |
sin |
2 |
B) |
|
|
|
|
|
|
2 |
|
|
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Із (2.17) отримаємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
cosB |
|
|
|
|
1 |
e2 |
|
|
|||
V |
1 e2 |
|
|
||||||||
|
|
|
|
|
|
. |
(3.80) |
||||
cosu |
|
|
|
|
|
||||||
|
|
|
1 e |
2 cos2 u |
|
||||||
138
Розділ 3. Розв'язування геодезичних задач
На основі (3.79) з врахуванням (3.80), а також помноживши чисельник і знаменник в (3.79) на a, отримуємо
du |
|
M |
1 |
|
. |
(3.81) |
||
dB |
a |
|
|
|
|
|||
|
1 e2 cos2 u |
|||||||
|
|
|
|
|
||||
Вираз (3.81) з врахуванням (3.77) буде
M |
1 |
|
M |
d |
, |
||
a |
|
|
|
|
ds |
||
|
1 e2 cos2 u |
||||||
|
|
|
|
||||
звідки
|
|
|
|
ds a |
1 e2 cos2 ud . |
(3.82) |
|
На основі (3.78) і (3.82)
N cosBdl acosu
 1 e2 cos2 u d ,
1 e2 cos2 u d ,
а, враховуючи, що acosu r N cosB , отримуємо
|
|
|
|
dl |
1 e2 cos2 u d |
(3.83) |
|
Інтегрування диференційних рівнянь Бесселя
Інтегруючи диференційні рівняння (3.82) і (3.83) уздовж дуги великого кола між її точками Q1 і Q2 , отримуємо
Q2 |
|
|
|
s a |
1 e2 cos2 u d , |
(3.84) |
|
Q1 |
|
|
|
139

Розділ 3. Розв'язування геодезичних задач
|
Q2 |
|
|
|
l L2 |
L1 |
1 e2 cos2 u d , |
(3.85) |
|
|
Q1 |
|
|
|
- еліптичні інтеграли, які в елементарних функціях не виражаються. З практичної точки зору це не є суттєвою перешкодою, поскільки можна знайти їх наближені вирази, придатні для обчислень з будь-якою, необхідною для практики, точністю.
Враховуючи вимоги обчислювальної практики з використанням сучасної комп’ютерної техніки, доцільно для наближеного інтегрування рівнянь Бесселя застосувати розклад підінтегральних виразів в ряди, що швидко сходяться, з наступним почленним інтегруванням рядів.
Почнемо з інтегралу (3.84). Передусім перетворимо його підінтегральну функцію, виразивши її аргумент - приведену широту – через змінну .
Звернемось до рис.3.10, на якому із точки P' проведено дугу великого кола перпендикулярно до продовження дуги
Q1'Q2 '.
Утворився прямокутний трикутник P'Q1'Q3 ', катети якого P'Q3 ' k і Q1'Q3 ' 90o M знайдуться за формулами
sinm sin A1 cosu1, |
(3.86) |
|||
tgM |
|
tgu1 |
. |
(3.87) |
|
|
|||
|
|
cos A |
|
|
|
1 |
|
|
|
Із прямокутного трикутника Q2 'P'Q3 ', розглядаючи |
||||
точку Q2 ' як точку на дузі |
великого кола |
Q1'Q3 ', тобто з |
||
широтою u, запишемо |
|
|
|
|
sinu cosmsin(M ), |
(3.88) |
|||
звідки |
|
|
|
|
140

Розділ 3. Розв'язування геодезичних задач |
|
cos2 u 1 cos2 msin2 (M ). |
(3.89) |
P
m
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|||||
|
|
A1 |
|
|
|
|
|
|
|
|
|
900-(M+ ) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
90 -M |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.10 |
|||||||
Тепер перетворимо рівняння (3.84) |
|||||||||||||||||||
|
Q2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 e2 cos2 |
msin2 (M ) d |
||||||||||||||||
s a 1 e |
|||||||||||||||||||
|
Q1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Q |
|
|
|
|
|
e |
2 |
|
|
|
|
|
|
|
|
|
a 1 e2 2 |
|
1 |
|
|
|
|
|
cos2 msin2 (M ) d . |
|||||||||||
1 e |
2 |
|
|
||||||||||||||||
|
|
|
Q1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
e2 |
|
|
|
|
|
|
|
||||||||
Враховуємо, що |
|
|
|
|
|
e'2 , a 1 e2 b, де b мала |
|||||||||||||
|
|
e2 |
|||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||
піввісь еліпсоїда; тоді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s b 2 |
1 e'2 cos2 |
msin2(M ) d . |
||||||||||||||||
|
|
Q1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
141
