
Математика Лабораторный практикум часть 2
.pdfЗаконом распределения с.в. называется правило, которое связывает значения с.в. и соответствующие им вероятности. Закон распределения д.с.в. можно задать с помощью ряда или функции распределения. Рядом распределения д.с.в. ξ называется таблица, в верхней строке которой перечислены все значения с.в., а в нижней – вероятности этих значений.
ξ |
х1 |
x2 |
… |
xn |
… |
P |
р1 |
р2 |
… |
pn |
… |
При этом pn 1. Функцией распределения с.в. ξ называется ве-
роятность того, что она примет значение меньше, чем заданное x:
F(x) P( x) .
Закон распределения непрерывной с.в. можно задать с помощью плотности или функции распределения. Плотностью распределения непрерывной с.в. называется первая производная от функции распределения: p(x) F (x) (предполагается, что функция распределения дифференцируема при всех действительных х за исключением, быть может, конечного числа точек).
Отметим некоторые свойства плотности и функции распределе-
ния.
x
1) F(x) p(x)dx;
2) p(x)dx 1;
3) P( ) p(x)dx F( ) F( ).
Математическим ожиданием дискретной с.в. ξ называется её
n
среднее значение M xi pi (если множество значений с.в. счётно,
i 1
то рассматривается числовой ряд).
Математическим ожиданием непрерывной с.в. ξ называется её
|
|
|
|
|
|
среднее значение M |
xp(x)dx . |
|
|
||
|
|
|
|
|
|
Дисперсией с.в. ξ называется среднее значение квадрата |
|||||
отклонения |
с.в. |
от |
её |
математического |
ожидания: |
D M( M )2 M 2 (M )2 . |
|
|
|
||
11

n |
n |
Для дискретной с.в. D (xi M )2 pi |
xi2 pi (M )2 (если |
i 1 |
i 1 |
множество значений с.в. счётно, то рассматривается числовой ряд).
|
|
|
Для непрерывной с.в. D |
(x M )2 p(x)dx |
x2 p(x)dx (M )2 . |
|
|
|
Примеры распределений с.в.
1) Пусть Х – число успехов в схеме Бернулли (n – число испытаний, p – вероятность успеха, q=1–p). Тогда закон распределения случайной величины Х задаётся соответствием xi pi Cni piqn i , i=0, …, n. Этот закон называется биномиальным. Для этого распределения математическое ожидание и дисперсия M(X) np, D(X) npq.
2) Случайная величина Х называется равномерно распределённой на отрезке [a, b], если её плотность распределения имеет вид:
|
1 |
при a x b, |
|
|
|
|
||
p(x) b a |
|
|
|
0 |
при x a, x b. |
|
||
График плотности и функции распределения приведены на рисунке 1.
а) |
б) |
Рис. 1. График плотности и функции распределения:
а – график плотности распределения; б – график функции распределения
|
a b |
|
|
(b a)2 |
||
Для равномерного распределения M(X) |
|
, |
D(X) |
|
. |
|
2 |
12 |
|||||
|
|
|
|
|||
Экспоненциальное (или показательное) распределение имеет пло-
тность распределения вида:
e x |
при |
x 0, 0, |
|
p(x) |
0 |
при |
x 0. |
|
|||
Например, из практики известно, что время безотказной работы телевизора распределено по показательному закону. Смысл параметра в том, что число 1/ равно среднему времени безотказной работы телевизора.
12

Рис. 2. График плотности экспоненциального распределения
Математическое ожидание и дисперсия показательного распреде-
ления, соответственно, равны: M(X) 1 , D(X) 1 .
2
Случайная величина Х называется нормально распределённой (имеющей распределение Гаусса), если её плотность вероятности имеет вид:
p x |
|
1 |
|
e |
x a 2 |
0. |
||
|
|
2 2 |
, |
|||||
|
|
|
|
|||||
|
|
2 |
||||||
|
|
|
|
|
|
|
||
Нормальное распределение будем обозначать N (a, ). Тогда X N(a, ) означает, что с.в. X имеет нормальное распределение с параметрами a, . Плотность зависит от двух параметров a и > 0. Если параметры a = 0, σ = 1, то такая нормально распределённая случайная величина называется стандартной нормальной случайной величиной.
Математическое ожидание и дисперсия нормального распределения, соответственно, равны: M(X) а, D(X) 2 .
Функция распределения равна:
F x |
|
1 |
|
x |
u a 2 |
|
|
|
|
|
|||||
|
|
e 2 2 du. |
|||||
|
|
|
|
||||
|
|
||||||
|
|
2 |
|||||
График плотности нормального распределения изображён на рисунке 3.
Рис. 3. График плотности нормального распределения
13
В природе часто встречаются нормально распределённые с.в. Так, «естественные» размеры человека (рост, вес и т.д.), деревьев (высота, диаметр ствола) распределены нормально.
Задание1. Для данной дискретной случайной величины построить многоугольник распределения, найти функцию распределения и построить её график. Найти математическое ожидание и дисперсию.
Варианты заданий
Вариант 1
|
X |
-5 |
2 |
4 |
7 |
13 |
|
P |
0,3 |
0,1 |
0,25 |
0,15 |
0,2 |
Вариант 2 |
|
|
|
|
|
|
|
X |
-4 |
-2 |
0 |
1 |
3 |
Вариант 3 |
P |
0,2 |
0,25 |
0,2 |
0,15 |
0,2 |
|
|
|
|
|
|
|
|
X |
-5 |
-2 |
0 |
7 |
8 |
|
P |
0,2 |
0,3 |
0,1 |
0,25 |
0,15 |
Вариант 4 |
|
|
|
|
|
|
|
X |
-7 |
-4 |
-2 |
0 |
3 |
|
P |
0,35 |
0,15 |
0,2 |
0,1 |
0,2 |
Вариант 5 |
|
|
|
|
|
|
|
X |
-6 |
-3 |
0 |
2 |
5 |
|
P |
0,25 |
0,2 |
0,1 |
0,2 |
0,25 |
Вариант 6 |
|
|
|
|
|
|
|
X |
0 |
2 |
4 |
7 |
8 |
|
P |
0,3 |
0,1 |
0,2 |
0,05 |
0,35 |
Вариант 7 |
|
|
|
|
|
|
|
X |
-5 |
-2 |
0 |
7 |
8 |
|
P |
0,3 |
0,25 |
0,1 |
0,05 |
0,3 |
Вариант 8 |
|
|
|
|
|
|
|
X |
-2 |
-1 |
4 |
5 |
7 |
|
P |
0,3 |
0,15 |
0,2 |
0,1 |
0,25 |
14
Вариант 9
|
X |
1 |
2 |
4 |
5 |
8 |
|
P |
0,3 |
0,3 |
0,15 |
0,05 |
0,2 |
Вариант 10 |
|
|
|
|
|
|
|
X |
-6 |
-5 |
-3 |
-2 |
0 |
|
P |
0,2 |
0,2 |
0,1 |
0,35 |
0,15 |
Вариант 11 |
|
|
|
|
|
|
|
X |
-3 |
-1 |
0 |
2 |
3 |
|
P |
0,1 |
0,2 |
0,15 |
0,05 |
0,5 |
Вариант 12 |
|
|
|
|
|
|
|
X |
-5 |
-4 |
-2 |
0 |
1 |
|
P |
0,4 |
0,2 |
0,1 |
0,1 |
0,2 |
Вариант 13 |
|
|
|
|
|
|
|
X |
-1 |
0 |
3 |
5 |
8 |
|
P |
0,3 |
0,15 |
0,2 |
0,05 |
0,3 |
Вариант 14 |
|
|
|
|
|
|
|
X |
-5 |
-3 |
0 |
3 |
9 |
|
P |
0,3 |
0,25 |
0,1 |
0,05 |
0,3 |
Вариант 15 |
|
|
|
|
|
|
|
X |
-4 |
0 |
2 |
3 |
5 |
|
P |
0,3 |
0,1 |
0,25 |
0,15 |
0,2 |
Вариант 16 |
|
|
|
|
|
|
|
X |
-2 |
-1 |
0 |
1 |
4 |
|
P |
0,2 |
0,25 |
0,2 |
0,15 |
0,2 |
Вариант 17 |
|
|
|
|
|
|
|
X |
-5 |
-1 |
0 |
4 |
5 |
|
P |
0,2 |
0,3 |
0,1 |
0,25 |
0,15 |
Вариант 18 |
|
|
|
|
|
|
|
X |
-8 |
-6 |
-4 |
-3 |
1 |
|
P |
0,35 |
0,15 |
0,2 |
0,1 |
0,2 |
15
Вариант 19
|
X |
-3 |
-2 |
0 |
2 |
3 |
|
P |
0,25 |
0,2 |
0,1 |
0,2 |
0,25 |
Вариант 20 |
|
|
|
|
|
|
|
X |
-1 |
2 |
4 |
5 |
9 |
|
P |
0,3 |
0,1 |
0,2 |
0,05 |
0,35 |
Вариант 21 |
|
|
|
|
|
|
|
X |
-3 |
-2 |
1 |
3 |
5 |
|
P |
0,3 |
0,25 |
0,1 |
0,05 |
0,3 |
Вариант 22 |
|
|
|
|
|
|
|
X |
-3 |
-1 |
1 |
2 |
6 |
|
P |
0,3 |
0,15 |
0,2 |
0,1 |
0,25 |
Вариант 23 |
|
|
|
|
|
|
|
X |
-11 |
-6 |
-2 |
0 |
2 |
|
P |
0,3 |
0,3 |
0,15 |
0,05 |
0,2 |
Вариант 24 |
|
|
|
|
|
|
|
X |
-1 |
0 |
1 |
4 |
10 |
|
P |
0,2 |
0,2 |
0,1 |
0,35 |
0,15 |
Вариант 25 |
|
|
|
|
|
|
|
X |
-3 |
-1 |
1 |
2 |
5 |
|
P |
0,1 |
0,2 |
0,15 |
0,05 |
0,5 |
Вариант 26 |
|
|
|
|
|
|
|
X |
-2 |
-1 |
0 |
2 |
4 |
|
P |
0,1 |
0,2 |
0,15 |
0,15 |
0,4 |
Вариант 27 |
|
|
|
|
|
|
|
X |
-2 |
-1 |
1 |
3 |
6 |
|
P |
0,1 |
0,2 |
0,3 |
0,2 |
0,2 |
Вариант 28 |
|
|
|
|
|
|
|
X |
-3 |
-1 |
1 |
2 |
5 |
|
P |
0,3 |
0,1 |
0,1 |
0,3 |
0,2 |
16
Вариант 29
|
X |
-4 |
-1 |
1 |
3 |
5 |
|
P |
0,2 |
0,1 |
0,15 |
0,15 |
0,4 |
Вариант 30 |
|
|
|
|
|
|
|
X |
-2 |
0 |
1 |
2 |
4 |
|
P |
0,3 |
0,1 |
0,2 |
0,1 |
0,3 |
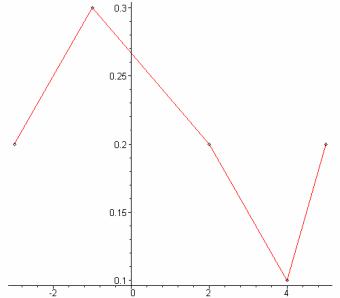
Пример выполнения задания 1
Дан ряд распределения случайной величины.
X |
-3 |
-1 |
2 |
4 |
5 |
P |
0,2 |
0,3 |
0,2 |
0,1 |
0,2 |
>restart;with(stats):with(describe):with(plots):
Вводим значения случайной величины:
>X:=[-3,-1,2,4,5];n:=count(X);
X:=[-3,-1,2,4,5] n:=5
Вводим соответствующие вероятности: > P:=[0.2,0.3,0.2,0.1,0.2];
P:=[0.2,0.3,0.2,0.1,0.2]
Проверка корректности задания случайной величины:
> sum('P[i]','i'=1..n);
1.0
Строим многоугольник распределения:
>a:=pointplot([[X[1],P[1]],[X[2],P[2]],[X[3],P[3]],[X[4],P[4]],[X[5],P[5]]]):
>b:=plot([[X[1],P[1]],[X[2],P[2]],[X[3],P[3]],[X[4],P[4]],[X[5],P[5]]]): > display([a,b]);
17
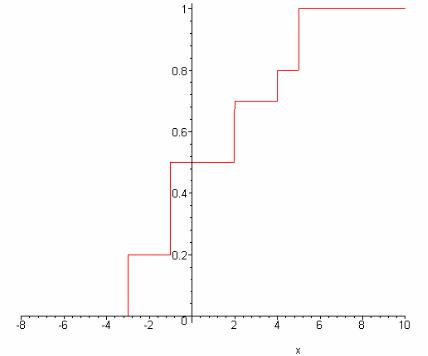
Запишем функцию распределения случайной величины X и построим её график.
> F:=piecewise(x<=X[1],0,x>X[1]and x<=X[2],P[1],x>X[2]and x<=X[3],P[1]+P[2],x>X[3]and x<=X[4],P[1]+P[2]+P[3],x>X[4]and x<=X[5], P[1]+P[2]+P[3]+P[4],x>X[5],P[1]+P[2]+P[3]+P[4]+P[5]);
0 |
x 3 |
0.2 |
3 x and x 1 |
|
1 x and x 2 |
0.5 |
|
F : |
2 x and x 4 |
0.7 |
|
0.8 |
4 x and x 5 |
|
5 x |
1.0 |
> plot(F,x=X[1]-5..X[n]+5);
Найдём математическое ожидание случайной величины X:
> MO:=sum('X[i]*P[i]','i'=1..n);
MO:=0.9
Найдём дисперсию X:
> Dis:=sum('(X[i])^2*P[i]','i'=1..n)-M^2;
Dis:=8.69
Задание 2. Задана плотность p(x) распределения непрерывной случайной величины . Требуется:
18
а) найти параметр c;
б) найти функцию распределения случайной величины ; в) построить графики функции и плотности распределения слу-
чайной величины ; г) найти математическое ожидание и дисперсию случайной ве-
личины ; д) найти вероятность того, что случайная величина примет
значение в интервале (a;b).
Варианты заданий
|
|
0, |
|
x [2;5], |
|
|
Вариант 1. |
p(x) c(x 2)3, |
x [2;5]., |
a 1; |
b 3. |
||
|
|
|
|
|
|
|
Вариант 2. |
|
0, |
|
x [0;3], |
a 2; |
b 3. |
p(x) |
|
|
, |
|||
|
2cx2, |
|
x [0;3]. |
|
|
|
|
|
0, |
|
x [ 1;2], |
|
|
Вариант 3. |
p(x) c(x 1)3, |
x [ 1;2]., |
a 1; |
b 3. |
||
|
|
|
|
|
|
|
Вариант 4. |
0, |
|
x [0;2], |
a 1; |
b 3. |
|
p(x) |
|
|
, |
|||
|
cx3, |
x [0;2]. |
|
|
||
|
|
|
|
|
|
|
Вариант 5. |
|
0, |
|
x [1;4], |
a 0; |
b 2. |
p(x) |
|
|
, |
|||
|
3c(x 1)2 |
, x [1;4]. |
|
|
||
|
|
|
|
|
|
|
Вариант 6. |
|
0, |
|
x [2;5], |
a 1; |
b 3. |
p(x) |
|
|
, |
|||
|
c(x 2)3, |
x [2;5]. |
|
|
||
|
|
|
|
|
|
|
Вариант 7. |
|
0, |
|
x [0;2], |
a 1; |
b 3. |
p(x) |
|
|
, |
|||
|
2cx3, |
|
x [0;2]. |
|
|
|
Вариант 8. |
|
0, |
|
x [2;5], |
a 1; |
b 4. |
p(x) |
|
|
, |
|||
|
c(x 2)3, |
x [2;5]. |
|
|
||
|
|
|
|
|
|
|
19
|
|
|
0, |
x [2;5], |
a 1; |
b 3. |
||
Вариант 9. p(x) |
|
|
|
|
, |
|||
|
c(x 1), |
x [2;5]. |
|
|
||||
Вариант 10. |
p(x) |
|
0, |
|
|
x [2;5], |
a 1; |
b 4. |
|
|
|
|
, |
||||
|
|
c(x 2), |
|
|
x [2;5]. |
|
|
|
Вариант 11. |
|
|
0, |
|
|
x [4;6], |
a 5; |
b 7. |
p(x) |
|
, |
, |
|||||
|
|
c(x 3)3 |
x [4;6]. |
|
|
|||
|
|
|
|
|
|
|
|
|
Вариант 12. |
p(x) |
|
0, |
|
|
x [2;5], |
a 1; |
b 4. |
|
|
|
|
, |
||||
|
|
c(x 4), |
|
|
x [2;5]. |
|
|
|
Вариант 13. |
|
|
0, |
|
|
x [2;6], |
a 1; |
b 3. |
p(x) |
|
|
, |
, |
||||
|
|
c(x 2)2 |
x [2;6]. |
|
|
|||
|
|
|
|
|
|
|
|
|
Вариант 14. |
|
0, |
|
x [3;5], |
a 1; |
b 4. |
||
p(x) |
|
|
|
, |
||||
|
c(x 2), |
x [3;5]. |
|
|
||||
Вариант 15. |
|
0, |
|
x [5;8], |
a 6; |
b 7. |
||
p(x) |
|
|
|
, |
||||
|
c(x 5), |
x [5;8]. |
|
|
||||
Вариант 16. |
p(x) |
|
0, |
|
|
x [2;6], |
a 3; |
b 5. |
|
|
|
|
, |
||||
|
|
c(x 3), |
|
x [2;6]. |
|
|
||
Вариант 17. |
|
|
0, |
|
|
x [2;7], |
a 1; |
b 5. |
p(x) |
|
|
|
, |
||||
|
|
c(x 2)2 |
, x [2;7]. |
|
|
|||
|
|
|
|
|
|
|
|
|
Вариант 18. |
p(x) |
|
0, |
|
|
x [2;6], |
a 3; |
b 4. |
|
|
|
|
, |
||||
|
|
c(x 5), |
|
x [2;6]. |
|
|
||
Вариант 19. |
|
|
0, |
|
x [1;5], |
a 2; |
b 4. |
|
p(x) |
cx2, |
|
|
, |
||||
|
|
|
|
x [1;5]. |
|
|
||
20
