Демина Тселые и мероморфные функтсии 2015

5. Периодические мероморфные функции

Шаг 3. Записать общее выражение для эллиптического решения w(z), имеющего K попарно различных полюсов a1, . . ., aK в параллелограмме периодов с рядами Лорана w(1)(z − a1),

. . ., w(K)(z − ak) в окрестности этих полюсов (см. выражение (5.18)), и найти ряды Лорана для функции w(z), заданной равенством (5.18), в окрестности ее полюсов a1, . . ., aK , положив без ограничения общности a1 = 0. При этом удобно ввести обозначения:

def		def
Aj = (aj), Bj			= z(aj), j = 2, . . . , K;
	K		K	(5.40)
def	∑		∑j
H0 = h0	−	c−(j1)	ζ(aj) − c−(j2)	(aj).
	j=2		=2

Шаг 4. Потребовать, чтобы ряды Лорана, найденные на третьем шаге, совпадали с соответствующими рядами Лорана, выбранными на втором шаге. Составить алгебраическую систему, добавив к ней уравнения Bj2 = 4A3j − g2Aj − g3, j =

=2, . . ., K, являющиеся результатом подстановок z(aj) =

=Bj, (aj) = Aj в соотношение (5.36). Количество уравнений в системе должно быть не меньше, чем число параметров искомого эллиптического решения. Решить алгебраическую систему относительно параметров эллиптического решения w(z).

Другими словами, найти H0, g2, g3, {A2, . . . , AK }, {B2, . . . , BK }. При этом могут появиться ограничения на параметры исходного уравнения (5.35). Если система несовместна, то уравнение (5.35) не имеет эллиптических решений (5.41) с выбранными рядами Лорана.

Шаг 5. Используя теорему сложения (5.22) для эллиптической функции Вейерштрасса (z) и соотношение (5.23) для функции ζ(z), а также свойства четности (нечетности)

61

5. Периодические мероморфные функции

соответствующих функций, переписать выражение (5.18) в виде

w(z) =

K

mj

(−1)kc−(jk) dkk−22

∑∑

(k − 1)!

dz −

j=2 k=2

K

(j)

(z) + {

p1

k

(1)

∑

c

∑

(

−

−

+

−

1

Fj

−

k

2

k=2

(k

1)!

j=2

где

Fj(z) =

z(z) + Bj

,

(z) − Aj

[		4				−	]
		1		Fj2(z)			(z)
−							(5.41)
	dk		2		} (z) + H0,
	dzk−2

j = 2, . . . , K.

(5.42)

Провести проверку полученных решений, подставляя их вместе с найденными ограничениями в исходное уравнение (5.35).

Далее заметим, что уравнению (5.35) могут удовлетворять ряды Лорана с произвольными коэффициентами. Если такие ряды выбраны на втором шаге, то для удобства эти произвольные коэффициенты также вносятся в список параметров искомого эллиптического решения. В дополнение: на четвертом шаге метода алгебраическую систему можно построить следующим образом. Необходимо подставить ряды

Лорана, найденные		на	третьем	шаге,	в исходное		уравнение
и	приравнять нулю		коэффициенты		при	отрицательных
и	нулевой степенях	переменных		(z − aj), j		=	1, . . . , K в

получившемся соотношении. Этот подход учитывает тот факт, что эллиптическая функция без полюсов является постоянной. На «нулевом уровне» достаточно взять всего одно соотношение. Заметим, что в этом случае получающаяся алгебраическая система является конечной. Предположим, что при построении выражения (5.18) хотя бы один из рядов с произвольными коэффициентами используется несколько раз. В этой ситуации алгебраическая система не содержит параметров, соответствующих этим произвольным коэффициентам, и необходимо проверять, являются ли такие ряды различными,

62

5. Периодические мероморфные функции

особенно если алгебраическая система формируется с помощью только что описанного подхода.

Если эллиптическая функция w(z) имеет два или более различных полюса в параллелограмме периодов, то для построения рядов Лорана на третьем шаге необходимо использовать теоремы сложения для функций (z), z(z) и формулу сложения для функции ζ(z). В наших обозначениях эти соотношения выглядят следующим образом:

ζ(ai,j) = ζ(ai) − ζ(aj) +

Bi + Bj

,

2(Ai − Aj)

(ai,j) = −Ai − Aj +

(Bi + Bj)2

(5.43)

,

4(Ai − Aj)2

Bi (Bi + Bj)2

(a

) =

−

B +

(Bi + Bj)(12Ai2 − g2)

−

,

2(Ai − Aj)3

z

i,j

i

4(Ai − Aj)2

где ai,j =

ai

− aj. Значения ζ(aj), j

=

2, . . ., K исчезают

из получающихся рядов при переходе от параметра h0 к параметру H0 по формуле (5.40) . Заметим, что соотношения

(5.43) непосредственно не	применимы, если Ai =	Aj или,
что то же самое, (ai)	= (aj). Эллиптическая	функция

Вейерштрасса (z) имеет второй порядок и, как следует из теоремы 5.2, принимает любое значение в параллелограмме периодов дважды. Таким образом, равенство (ai) = (aj) при ai ≠ aj возможно только для простых точек, другими словами,

z(ai) ≠ 0, z(aj) ≠ 0.

Выведем теоремы и формулу сложения для случая (ai) = = (aj), где ai ≠ aj. Пусть ω1 = 2τ1, ω2 = 2τ2 – основные периоды эллиптической функции Вейерштрасса (z). Символом τ3 обозначим сумму τ1 + τ2. Двойными для функции (z) являются точки z = 0, z = τl, l = 1, 2, 3, при этом начало координат z = 0 – двойной полюс. Следовательно, ai ≠ τl, aj ≠ τl, l = 1, 2, 3. Из четности эллиптической функции Вейерштрасса(z) следует справедливость соотношения (2τl−z) = (z), l = 1,

63

5. Периодические мероморфные функции

2, 3. В результате мы получаем aj = 2τl −ai, где l = 3, если одна из точек (ai или aj) лежит внутри основного параллелограмма, и l = 1 или l = 2, если одна из точек лежит на стороне, определяемой соответствующим вектором τ1 или τ2. Число 2τl является периодом эллиптических функций (z), z(z), поэтому

(ai − aj) = (2ai), z(ai − aj) = (2ai) и z(ai) = − z(aj). Применяя правило Лопиталя в равенствах (5.43), мы находим формулу и теоремы сложения для случая (ai) = (aj):

ζ(a

) = ζ(a

)

−

ζ(a ) +

12Ai2 − g2

,

i,j

i

j

4Bi

(a

) = (2a

) =

−

2A

+

(12Ai2 − g2)2

,

16Bi2

i,j

j

i

(5.44)

(12Ai2 − g2)3

(a

) =

(2a ) =

−

B

i −

+

z

i,j

z

j

32Bi3

+

3(12Ai2 − g2)Ai

,

2Bi

где ai,j = ai

− aj. При решении

алгебраической системы

вычисления заметно упрощаются, если сначала найти величины ζ(ai − aj), (ai − aj), z(ai − aj), а затем использовать теоремы и формулу сложения (5.43) или (5.44).

Описанный метод позволяет находить любое эллиптическое решение уравнения (5.35) в силу того, что на третьем шаге используется общее выражение для эллиптического решения с соответствующими рядами Лорана. Если уравнению (5.35) удовлетворяет ровно N различных рядов Лорана вида (5.27), то

∑N

порядки эллиптических решений не превышают числа mi,

i=1

где m1, . . ., mN — порядки полюсов в соответствующих рядах. При выполнении условия g23 − 27g32 = 0 эллиптическая функция Вейерштрасса (z) вырождается, другими словами, становится простопериодической или рациональной, и, следовательно, вырождается и эллиптическое решение (5.41).

64

5. Периодические мероморфные функции

Теорема 5.8. Пусть алгебраическому автономному обыкновенному дифференциальному уравнению (5.35) с одним доминирующим дифференциальным мономом удовлетворяет конечное число рядов Лорана вида (5.27). Тогда мероморфные решения этого уравнения исчерпываются рациональными, простопериодическими, имеющими вид (5.10) при h(z) = = h0, и эллиптическими, причем суммарное число полюсов не превосходит количества различных рядов Лорана вида (5.27).

Вформулировке теоремы 5.8 для эллиптических и простопериодических решений необходимо учитывать только те полюсы, которые лежат в одном параллелограмме периодов и одной полосе периодов соответственно.

Вявном виде мероморфные решения, о которых идет речь в теореме 5.8, могут быть найдены последовательным перебором случаев двоякопериодических, простопериодических и рациональных решений. Алгоритм поиска простопериодических мероморфных решений вида (5.10) при h(z) = h0 и рациональных решений аналогичен описанному выше алгоритму поиска эллиптических решений. Отметим отличия. Сначала рассмотрим случай простопериодических решений. На втором шаге при выборе K различных рядов Лорана условие на вычеты (5.39) отбрасывается. На третьем шаге записывается общая формула для искомого решения w(z), имеющего K попарно

различных полюсов a1, . . ., aK в полосе периодов периодов с рядами Лорана w(1)(z − a1), . . ., w(K)(z − ak) в окрестности полюсов (см. выражение (5.10)). При разложении этой функции в ряды Лорана удобно ввести обозначения:

def π				πa		def π2
Aj =		ctg	(	j	),	L =		, j = 2, . . . , K.	(5.45)
	ω			ω			ω2

Параметры, подлежащие определению на четвертом шаге, имеют вид h0, L, {A2, . . . AK }. На пятом шаге теорема сложения

ctg(z − s) =	ctg z ctg s + 1			(5.46)
	ctg s	−	ctg z

65

5. Периодические мероморфные функции

позволяет переписать искомое решение в виде

m1

( 1)k−1c(1)

dk−1

w(z) = h0 + √

∑

−(k − 1)!−k

ctg (√

L

Lz)+

k=1

dzk−1

(5.47)

+√

K mj

(−1)k−1c−(jk)

dk−1

Aj ctg (√Lz)

+ √L

.

L

∑∑

k 1

−

(

)

(k − 1)!

dz −

j=2 k=1

Aj

√L ctg

√Lz

√

При вычислении квадратного корня L достаточно без ограничения общности выбрать любой знак. Как и в случае эллиптических решений, алгебраическую систему можно получить, подставив ряды Лорана, найденные на третьем шаге, в исходное уравнение и приравняв нулю коэффициенты при отрицательных и нулевой степенях переменных (z − aj), j = 1, . . . K в получившемся соотношении. Заметим, что в одной

полосе периодов не может быть двух точек ai ̸= aj таких, что
Нам	или ctg	(			)	(			)
Ai = Aj			√Lai			= ctg	√Laj .

осталось рассмотреть случай рациональных решений. На первом шаге в дополнении к рядам Лорана в окрестности конечных полюсов нужно построить ряды Лорана в окрестности бесконечно удаленной точки:

		mi,1			∞	d(i)
	(i)	∑	(i)	k	∑	−k	, εi,∞ < |z| < ∞,	(5.48)
w		(z) =	dk z		+
						zk
		k=1			k=0

где d(mi)i,1 ≠ 0, i = 1, . . . , M. Последовательно выбирая каждый из рядов Лорана в окрестности бесконечности, мы можем на третьем шаге получить выражения для искомых рациональных решений:

	mi0,1	K mj	c(j)
w(z) =	d(i0)zk +		−k		.	(5.49)
	k	(z		aj)k
	k=0	j=1 k=1
	∑	∑∑ −

66

5. Периодические мероморфные функции

Далее в равенстве (5.49) без ограничения общности можно положить a1 = 0. Алгебраическая система составляется или путем сравнения соответствующих рядов, или подстановкой рядов Лорана в исходное уравнение. В последнем случае необходимо дополнительно требовать обращения в нуль коэффициентов при положительных и нулевой степенях переменной z для ряда в окрестности бесконечности.

Таким образом, поиск мероморфных решений алгебраических обыкновенных дифференциальных уравнений, удовлетворяющих условиям теоремы (5.8), состоит в последовательном переборе вариантов. Рассмотрим примеры. Заметим, что ниже нас будут интересовать непостоянные мероморфные решения.

Задача 5.1. Найти все мероморфные решения алгебраического автономного обыкновенного дифференциального уравнения

wzz + wwz − 6w3 + αw2 + βw + γ = 0.

(5.50)

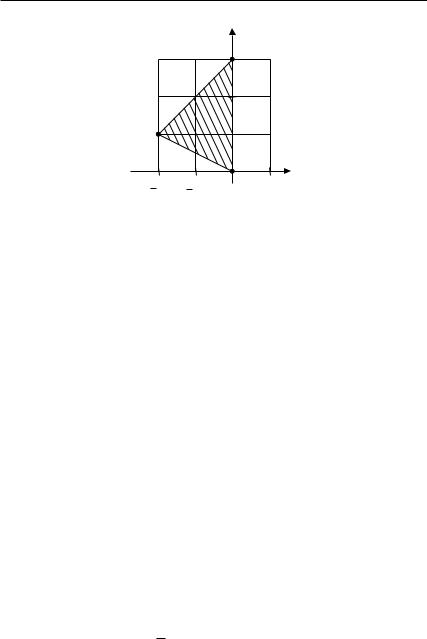
Решение. Уравнение (5.50) содержит один доминирующий моном: −6w3 и, следовательно, не может иметь целых трансцендентных решений. Согласно алгоритму построения мероморфных решений найдем все ряды Лорана в окрестности полюса z = 0, которые удовлетворяют уравнению (5.50). Построим многоугольник, соответствующий уравнению (5.50). При α = 0, β = 0, γ = 0 многоугольник представляет собой ребро, соединяющее точки Q1 = (−2, 1) и Q2 = (0, 3). Во всех остальных случаях многоугольник является треугольником с вершинами Q1 = (−2, 1), Q2 = (0, 3) и Q3, где

			(0, 0),	γ ̸= 0;
Q3	=		(0, 1),	γ = 0, β ̸= 0;	(5.51)
			(0, 2), γ = 0, β = 0, α ̸= 0.

На рис. 5.1 изображен многоугольник для случая γ ≠ 0.

67

5. Периодические мероморфные функции

		q2
		Q2
		3
		2
Q1		1
		Q3
2	1	0	1	q1

Рис. 5.1. Многоугольник уравнения (5.50) при γ ≠ 0.

Сначала рассмотрим укороченное уравнение для ребра, соединяющего точки Q1 и Q2:

		wzz + wwz − 6w3 = 0.					(5.52)
	Это уравнение имеет два степенных решения:
	(1)	1		(2)	2		(5.53)
	w (z) = 2z , w (z) = −				3z .

Найдем первую вариацию от выражения E1 = wzz + wwz − 6w3.

Имеем
d2	d	2

						(5.54)
	L (E1) = dz2 + w dz + wz − 18w .

Действуя оператором (5.54) на степенную функцию zj и подставляя вместо w(z) соответствующие асимптотики, получим:

()

L (E1) w=	21z		z j = j −	5		(j + 2)zj−2,	(5.55)
				2
			z j = (j −	11
L (E1) w=−	32z						(5.56)
				3 )(j + 2)zj−2.

68

5. Периодические мероморфные функции

Ни в одном случае мы не нашли целых индексов Фукса j > − −1. Следовательно, для уравнения (5.50) существуют только два различных ряда Лорана в окрестности полюса z = 0:

1			∞	(1)	2			∞	(2)
w(1)(z) =		+	∑	ck zk,	w(2)(z) = −		+	∑	ck zk. (5.57)
	2z		k=0			3z		k=0

Все коэффициенты этих рядов могут быть последовательно вычислены. Уравнение (5.50) не может иметь эллиптических решений, поскольку не выполняется необходимое условие (5.19).

Тогда будем искать простопериодические мероморфные

решения. Начнем со случая, когда решения имеют полюсы только одного типа (с вычетами c(1)−1 = 1/2 или c(2)−1 = −2/3).

Такие решения следует искать в виде

√			(√			)
w(z) = L(j)c−(j1) ctg				L(j)z		+ h0(j), j = 1, 2.	(5.58)

Разложим функцию (5.58) в ряд Лорана в окрестности точки z = 0

w(z) =	c−1	+ h0 −	c−1L	z + O (|z|	3	), 0 < |z| < εj	(5.59)
	z		3

и, подставив этот ряд в исходное уравнение, приравняем нулю выражения, стоящие при неположительных степенях переменной z. В результате придем к системе трех уравнений:

c−1α − h0(18c−1 + 1) = 0,
6c−2	1L + 2αh0 − 18h02 + β = 0,	(5.60)
2c−2 1L {18h0 − α} − h0Lc−1 + 3γ+
+3h0 {β + αh0 − 6h02} = 0.

В равенствах (5.59), (5.60) мы опустили верхний индекс. Первое из этих уравнений мы можем решить относительно h0, второе –

69

5. Периодические мероморфные функции

относительно L. Имеем:
(1)		α			L(1)	= −	11α2 + 200β
h0	=		,							;
		20						300
		2α						20α2 + 363β		(5.61)
(2)					L(2)	= −
h0	=			,						.
		33						968

Наличие третьего уравнения говорит о том, что исходное дифференциальное уравнение имеет мероморфные решения вида (5.58) не при всех значениях параметров α, β, γ. Решая третье уравнение из системы (5.60), находим следующие ограничения на параметры:

(1)	(α2	+ 25β)α		(2)	(4α2	+ 121β)α		(5.62)
γ = −				γ = −
		375	,			2662 .

Далее будем строить простопериодические мероморфные решения, имеющие одновременно полюсы как первого, так и второго типа. Общее выражение для таких решений выглядит следующим образом:

√ ( {√ } {√ })

w(z) = L c(1)−1 ctg Lz + c(2)−1 ctg L(z − a) + h0. (5.63)

Без ограничения общности мы считаем, что точка z = 0 является полюсом первого типа, а точка z = a — второго. Раскладывая функцию (5.63) в ряды Лорана в окрестности точек z = 0 и z = = a, получим:

1

2A

+ h0 + (

L

2

)z +

2A

(

w(z) =

+

+

2A

L + A2

z2

+ o(|z|2),

2z

3

2

3

3

2

A

5L

A2

)

w(z) =

−

+

+ h0

−

{

+

}(z − a)+

3(z − a)

2

18

2

A

+

(L + A2)(z − a)2 + o(|z − a|2).

2

def

√

√

Здесь мы ввели обозначение

A

L ctg

La . Подставляя

=

( )

эти ряды в исходное уравнение и приравнивая нулю выражения,

70