Иванов Криптографические методы засчиты информации в компютерных 2012

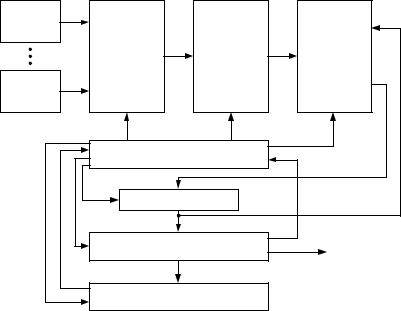
	питания желательно хранить часть внутреннего секретного со-
	стояния блока генерации или ключ в энергонезависимой памя-
	ти. Это позволит генератору при перезапуске оказаться в не-
	предсказуемом состоянии. В промежутке между соседними об-
	новлениями ключа устройство суть генератор гаммы поточного
	режима блочного шифра.
	Источник
	энтропии
	1
	Блок		Накопитель	Блок
	хеширования			хеширования
	Источник
	энтропии
	n
		Блок управления
		Ключ
		Блок генерации		ПСП
	Блок оперативного и тестового
		контроля
	Рис. 8.4. Аппаратно-программный комплекс генерации ПСЧ,
	использующий внешние источники случайности

Синхронизацию работы всех блоков генератора, а также определение моментов инициирования процедуры обновления ключа обеспечивает блок управления. Процедура обновления инициируется при накоплении достаточного количества энтропии и возникновении одного из трех событий:

1)наступило время планового обновления ключа;

2)блок генерации оказался в «слабом» состоянии, из которого в течение длительного времени не может выйти самостоятельно;

241

3) обнаружены нарушения статистической безопасности выходной последовательности.

Функции блока оперативного и тестового контроля: проверка работоспособности (методом сравнения с эталоном) устройства в заданные моменты времени (при включении питания, по запросу пользователя, периодическая и т.п.);

анализ статистической безопасности формируемых фрагментов выходной последовательности, в том числе анализ корреляции между соседними выборками; анализ ключа и внутреннего состояния блока генерации на

предмет попадания в пространство «слабых» значений; информирование блока управления о проблемах в работе блока генерации (например, о необходимости обновления ключа).

Блочные генераторы ПСЧ следует признать лучшими по совокупности двух критериев – непредсказуемости и быстродействию.

Поточные генераторы ПСЧ, являясь самыми быстродействующим типом генераторов (в ущерб остальным характеристикам), применяются в тех случаях, когда необходима передача больших информационных потоков в реальном масштабе времени или близком к нему.

В отличие от блочных генераторов ПСЧ, чьи нелинейные функции строятся по итеративному принципу, при проектировании поточных генераторов используется огромное множество приемов и методов, классифицировать которые очень сложно. Можно выделить всё же следующие параметры:

способ управления синхронизацией; механизм получения выходной последовательности; тип используемых S- или R-блоков;

наличие или отсутствие каскадов.

Способ управления синхронизацией. По этому параметру ге-

нераторы делятся на две группы: работающие по принципу stop- and-go и не использующие управления синхронизацией. Классические примеры генераторов ПСЧ первой группы – генераторы ПСЧ А5 и PIKE.

242

Механизм получения выходной последовательности. По этому параметру генераторы можно разделить на две группы – соответственно использующие и не использующие для получения результирующей последовательности комбинирование нескольких ПСП. Классический пример первого подхода – перемешивание двух ПСП под управлением третьей. Примерами генераторов первого типа являются упомянутые выше генераторы А5 и PIKE, в которых комбинирование осуществляется с использованием операции сложения по модулю 2.

Тип испольуемых S- или R-блоков. По этому параметру генера-

торы можно разделить на четыре группы:

1)вообще без табличных преобразований;

2)использующие фиксированные несекретные таблицы;

3)использующие фиксированные секретные (ключевые или зависящие от ключа) таблицы;

4)использующие секретные таблицы, непрерывно изме-

няющиеся в процессе функционирования генератора. Последний вариант следует признать наиболее предпочтительным, так как он делает лишенными особого смысла действия аналитика, связанные с восстановлением ключевой таблицы по имеющемуся фрагменту ПСП. Классическим примером такого подхода является один из лучших поточных генераторов ПСЧ, генератор RC4, разработанный Р. Ривестом.

Наличие или отсутствие каскадов. По этому параметру ге-

нераторы можно разделить на две группы – по отсутствию либо наличию каскадов соответственно. В последнем случае принцип построения качественного генератора ПСЧ суть каскадное включение нескольких генераторов относительно невысокого качества.

Генераторы ПСЧ на основе односторонних функций сле-

дует признать наиболее математически обоснованным. Тем не менее эти генераторы не нашли широкого распространения в первую очередь по причине чрезвычайно низкого быстродействия. Они работают в сотни раз медленнее блочных генераторов ПСЧ, которые сами считаются медленными.

Непредсказуемые (криптографически стойкие) генераторы ПСЧ могут быть построены на основе использования в качестве нелинейного преобразования Ffb или Fout односторонних функ-

243

ций. Справедливо следующее утверждение: криптостойкие ге-

нераторы ПСЧ существуют тогда и только тогда, когда существуют односторонние функции [3, 4].

8.4. Генераторы на регистрах сдвига с линейными обратными связями

Вданном разделе описываются принципы построения наиболее эффективных (в первую очередь из-за простоты программной и аппаратной реализации и хороших статистических свойств) некриптографических генераторов ПСЧ. Используемый при их анализе математический аппарат – теория линейных последовательностных машин и теория конечных полей (полей Галуа).

Эти генераторы активно используются в качестве строительных блоков при построении поточных криптографических генераторов ПСП, помехоустойчивых кодов БЧХ, Рида–Соломона и других циклических кодов. Они обладают очень интересными свойствами, которые позволяют решать целый ряд специфических задач, связанных с обеспечением безопасности.

Вработе [29] теория двоичных последовательных генераторов на регистрах сдвига с линейными обратными связями (РСЛОС) обобщается на случай формирования недвоичных (L-ричных) последовательностей. Рассматриваются теоретические основы построения двоичных параллельных генераторов ПСЧ, недвоичные генераторов последовательного и параллельного типа, анализируются их свойства. Описываются принципы построения нелинейных генераторов произвольной длины, в том числе максимально возможной при заданном числе элементов памяти генератора, генераторов с предпериодом, генераторов с самоконтролем, универсальных программируемых генераторов.

8.4.1. Последовательные РСЛОС

Последовательности, формируемые двоичными генераторами на основе регистров сдвига с линейными обратными связями –

LFSR (Linear Feedback Shift Register), являются важнейшим классом ПСП. Основные достоинства этих генераторов:

244

простота программной и аппаратной реализации; максимальное быстродействие; хорошие статистические свойства формируемых последовательностей;

возможность построения на их основе генераторов, обладающих свойствами, ценными при решении специфических задач защиты информации (формирование последовательностей произвольной длины, формирование последовательностей с предпериодом, формирование ПСП с произвольным законом распределения, построение генераторов, обладающих свойством самоконтроля и т.п.).

РСЛОС, к сожалению, не являются непредсказуемыми, поэтому применяются при решении задач защиты компьютерных систем от умышленных деструктивных воздействий лишь в качестве строительных блоков.

Наиболее известные примеры использования РСЛОС и математического аппарата полей Галуа:

CRC-коды – идеальное средство контроля целостности информации при случайных искажениях информации; реализация концепции самотестирования БИС и СБИС; поточные алгоритмы А5, PANAMA, SOBER, SNOW и др.; блочный алгоритм RIJNDAEL, принятый в 2001 г. в качестве Американского стандарта шифрования ХХI века – AES. Исходная информация для построения двоичного РСЛОС –

так называемый образующий многочлен. Степень этого многочлена определяет разрядность регистра сдвига, а ненулевые коэффициенты – характер обратных связей.

В общем случае двоичному образующему многочлену степени N

Ф x ¦N	a xi (mod 2),
i 0	i
где aN a0 1, aj 0, 1`, j
		1, N -1 , соответствуют устройст-

ва, показанные на рис. 8.5,а (схема Фибоначчи) и 8.5,б (схема Галуа). Уравнения работы генераторов Фибоначчи и Галуа имеют вид соответственно

245

­ q		t 1			N a q t ;
°	1				¦ i i
°		t 1			i 1		t ,			(8.3)
®q j					q j 1
°
°		2, N ;
¯ j
­ q1		t 1			anqN t ;			q	t ,
°q	j	t 1			q	j 1	t a			(8.4)
®								N i 1 N
°
		2, N ,
¯ j

где qi(t) – состояние i-го разряда регистра в момент времени t,

i 1, N, или в матричной форме

				Q(t + 1) = T·Q(t),
			q1	t
	где	Q t	q2	t	– состояние генератора в момент времени t, а
			...
			qN t

Т – квадратная матрица порядка N вида (8.5) для генератора Фибоначчи или (8.6) для генератора Галуа

a1	a2 ...			aN 1	aN
1	0 ...			0	0
0	1 ...			0	0	(8.5)
		...
0	0 ...			1	0
0	...	0	0	aN
1	...	0	0	aN 1		(8.6)
	...
0	...	1	0	a2
0	...	0	1	a1

246

a0

a1

ai

aN - 1

aN

1	2	...	i	...	N
			i + 1		N - 1
			а

aN

aN - 1

ai

a1

a0

1	2	...	...	N
		N - i N - i + 1	N - 1
		б
		Блок сложения по модулю 2
		Блок умножения по модулю 2

Рис. 8.5. Общий вид LFSR, соответствующих

Ф(х) = aNхN + aN - 1хN - 1 +…+ a2х2 + a1х + a0, ai {0, 1}:

а– схема генератора Фибоначчи; б – схема генератора Галуа.

При ai = 1 умножение на ai равносильно наличию связи, при ai = 0 умножение на ai равносильно отсутствию связи

8.4.2. Параллельные РСЛОС

Рассмотренные последовательные LFSR могут использоваться только для генерации битовых ПСП. Если необходима n- разрядная последовательность, можно предложить два возможных метода решения.

В первом случае выбираем образующий многочлен степени N > n (еще лучше N >> n), выбираем схему Фибоначчи или Галуа и считываем очередной n-разрядный элемент ПСП с соседних разрядов регистра сдвига каждые n тактов работы LFSR. Недостатком такого решения очевидно является низкое быстродействие. Второй метод предполагает синтез схемы генератора, работающего в n раз быстрее исходного LFSR (иначе го-

247

воря, выполняющего за один такт своей работы преобразования, которые в исходном LFSR выполняются за n тактов). Второй вариант решения более эффективен с точки зрения затрат памяти и быстродействия при программной реализации в случае использования разреженного многочлена (многочлена с относительно небольшим числом ненулевых коэффициентов) Ф(х), в особен-

ности когда образующий многочлен генератора Фибоначчи имеет вид Ф(х) = хN + хj + 1, а i кратно n.

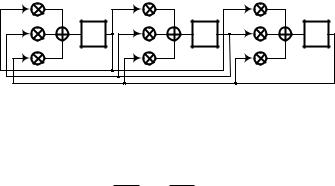
Исследуем свойства генератора многоразрядной ПСП. Общий вид генератора двоичных последовательностей, соответствую-

щего уравнению

Q(t + 1) = Tk Q(t),

показан на рис. 8.6.

	...	q1	...	qi	...	qN
	...		...		...

Рис. 8.6. Генератор двоичных последовательностей, соответствующий уравнению Q(t + 1) = Tk Q(t)

Величина, на которую происходит умножение в каждом блоке умножения (БУ), определяется соответствующим коэффициентом aij {0,1} сопровождающей матрицы

V = Tk ( i = 1, N , i = 1, N ).

Если aij = 0, это эквивалентно отсутствию связи между выходом i-го разряда регистра генератора и входом j-го сумматора по модулю два. Если aij = 1, это эквивалентно наличию связи между выходом i-го разряда регистра генератора и входом j-го сумматора по модулю два.

Так как нулевое состояние всех элементов памяти генератора является запрещенным, максимально возможное число состояний устройства, а значит, и максимально возможная длина формируемой двоичной последовательности, снимаемой с выхода любого разряда, равны 2N – 1. В этом случае диаграмма состояний генератора состоит из одного тривиального цикла и цикла максимальной длины 2N – 1.

248

Многочлен Ф(х) степени N называется примитивным, если он не делит нацело ни один многочлен вида хS – 1, где S < 2N – 1. Примитивные многочлены существуют для любого N. Показателем многочлена Ф(х) называется наименьшее натуральное число e, при котором xe – 1 делится на Ф(х) без остатка.

Пусть Ф(х) – примитивный многочлен степени N, тогда справедливо следующее утверждение.

Формируемая последовательность имеет максимальный период S = 2N – 1 тогда и только тогда, когда наибольший общий делитель чисел S и k равен 1 (т.е. S и k взаимно просты).

При k = 1 примитивность Ф(х) является необходимым и достаточным условием получения последовательности максимальной длины.

Последовательность максимальной длины принято называть М-последовательностью, а формирующий ее генератор – генератором М-последовательности. Именно генераторы М-последовательностей обычно используются для формирования ПСП. Список примитивных многочленов приведен в приложениях 1 и 2.

Каждая матрица V имеет характеристический многочлен

Μ(x), которым является определитель матрицы V – хE, т.е.

Μ(х) = V – хE , где Е – единичная матрица. Многочлен Ф(x)

определяет (образует) только структуру генератора, свойства же последнего зависят именно от Μ (x). Каждая квадратная

матрица удовлетворяет своему характеристическому уравнению, т.е. Μ (V) = 0. Характеристический и образующий мно-

гочлен генератора связаны следующим соотношением:

Μ (x) = Ф(х–1)хN,

т.е. являются взаимно-обратными. Примитивность Μ (x) авто-

матически означает примитивность Ф(х) и наоборот. Децимацией последовательности {qi(t)} по индексу k называ-

ется формирование новой последовательности {q*i(t)},

cостоящей из k-х элементов {qi(t)}, т.е. q*i(t) = qi(kt). Если период последовательности, полученной в результате децимации

М-последовательности, равен максимальному, децимация называется собственной или нормальной.

249

Последовательность, снимаемая с выхода i-го разряда генератора, изображенного на рис. 8.6, является децимацией по индексу k последовательности, снимаемой с выхода i-го разряда генераторов, изображенных на рис. 8.5. Если Q – начальное состояние генератора, то последовательности состояний, в которых будут находиться устройства в следующие моменты времени, имеют вид Q, QV, QV2 , QV3 , ... (для генератора, показанного на рис. 8.6) и Q, QT, QT2 , QT3 , ... (для генераторов, показанных на рис. 8.5). Учитывая, что V = Тk , можно сделать вывод, что в генераторе, показанном на рис. 8.6, за один такт осуществляются преобразования, которые в генераторах, показанных на рис. 8.5, – за k тактов. Таким образом, генератор, показанный на рис. 8.6, в котором содержимое первых k разрядов (при k ≤ N) полностью обновляется в каждом такте, может использоваться для генерации k-разрядной ПСП, что нельзя сказать про генераторы, показанные на рис. 8.5, которые в тех же разрядах формируют лишь сдвинутые копии одной и той же двоичной последовательности.

Пусть k = 1, F(х) – примитивный многочлен. Генераторы Галуа, образующий многочлен которых имеет вид

Ф(х) = (х + 1)F(х)

обладают свойством самоконтроля: при правильной работе генератора свертка по модулю два содержимого всех разрядов не меняет своего значения, иначе говоря, уравнение самоконтроля имеет вид

¦N	q t (mod 2) const.
i 1	i

8.4.3. Примеры двоичных РСЛОС

Рассмотрим примеры практической реализации генераторов ПСЧ, рассмотренных в данном разделе.

Двоичные последовательные РСЛОС. Пусть образующий многочлен имеет вид Ф(х) = х8 + х7 + х5 + х3 + 1. Этой ситуации соответствуют два генератора М-последовательности, показанные на рис. 8.7, а и б.

250