Введение в теорию фракталов (60

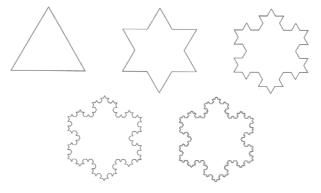
Отметим, что канторова пыль С×С×С, взвешенная в трехмерном пространстве, настолько «разрежена», что ее фрактальная размерность не достигает даже значения 2.

3.2. Снежинка Кох

Возьмем равносторонний треугольник и каждую из сторон разделим на три равные части, уберем средние части и достроим равносторонние треугольники, как показано на рис. 4. Продолжая процедуру для каждой вновь образованной стороны, после бесконечно большого числа итераций получим симметричную, похожую на снежинку, бесконечно изломанную кривую, называемую снежинкой Кох. Отличительной ее особенностью является то, что она, будучи замкнутой, нигде себя не пересекает.

Рис. 4

Вычислим фрактальную размерность снежинки по формуле (4). Покрытие исходного треугольника осуществляется тремя отрезками N(l) = 3 единичной длины l = 1. На следующем шаге соответст-

′	l	′	= 1/3. Тогда
венно имеем N(l ) =12,
				3
				ln
D = −				12			=	ln 4	≈1,26 .
				ln 3				ln 3
10

Это больше топологической размерности линии (n = 1), но меньше евклидовой размерности плоскости (n = 2), на которой расположена кривая. Вычислим длину кривой. На k-м шаге

Lk = 3 43 k

и при k → ∞ стремится к бесконечности. Таким образом, снежинка Кох представляет собой линию бесконечной длины, ограничивающую конечную площадь (нетрудно убедиться, что линия никогда не выходит за пределы окружности, описанной около исходного треугольника).

3.3. Салфетка и ковер Серпинского

Регулярный фрактал, называемый салфеткой Серпинского, получается последовательным вырезанием центральных равносторонних треугольников (рис. 5).

Рис. 5

В результате получается «дырявая» фигура, состоящая из бесконечного числа изолированных точек. Фрактальная размерность салфетки Серпинского равна

	D =	ln 3	≈1,58 .
		ln 2

Салфетка имеет нулевую площадь, поскольку в процессе ее построения была исключена площадь, в точности равная площади исходного треугольника. Об этом также говорит и значение размерности D < 2. Вычислим периметр исключенных областей. Если сторона исходного треугольника равна 1, то на первом шаге по-

11

строения периметр центрального треугольника равен 3/2. На втором шаге к нему добавляются три новых треугольника с общим периметром 9/4 и т. д. На k-м шаге периметр определяется суммой геометрической прогрессии

	k		3	s		3	k			3	k
	Pk = ∑				= 3			−1	≈ 3
			2			2				2
	s =1

и, очевидно, стремится к бесконечности.

Аналогично салфетке Серпинского можно построить квадратный ковер Серпинского (рис. 6).

Рис. 6

Его фрактальная размерность равна

= ln 8 ≈

D 1,89 . ln 3

Пространственным аналогом квадратного ковра Серпинского является губка Менгера (рис. 7).

Рис. 7

12

Ее фрактальная размерность равна

	D =	ln 2	≈ 2,73 .
		ln 3

Поскольку 2 < D < 3, это говорит о том, что губка имеет нулевой объем, но обладает бесконечной площадью поверхности своих пор.

4. ФРАКТАЛЫ В ФИЗИКЕ

Как было замечено Мандельбротом, природа любит фракталы ни чуть не меньше (если не больше) регулярных форм. На каждую гладкую кривую или поверхность в окружающем нас мире приходится много весьма нерегулярных, фрактальных кривых и поверхностей. Почему фракталы так распространены в природе? Решающей причиной, по-видимому, является то, что гладкая искривленная поверхность содержит свой внутренний масштаб – радиус кривизны. И естественно, такой внутренний масштаб должен иметь какую-то причину. Отсутствие естественных масштабов порождает самоподобие, а самоподобный объект является фракталом.

В качестве иллюстрации рассмотрим некоторые примеры физических фракталов. Это всего лишь «случайная выборка», бесконечно малая доля множества природных явлений, проявляющих фрактальные свойства: от распределения материи во Вселенной до электронной дифракции.

4.1. Клеточная размерность

На практике фрактальную размерность физического объекта можно определить, используя формулу (3). Обратимся снова к береговой линии на рис. 1. Подсчитывая число N(l) квадратов размером l, необходимых для покрытия фрактала при разных l (т. е. меняя размер ячейки сетки), можно определить фрактальную размерность береговой линии, измерив угловой коэффициент (наклон) графика ln N(l) как функции от ln l. Такой способ определения D

принято называть размерностью, определяемой по подсчету клеток

13

или клеточной размерностью. Например, для береговой линии Норвегии D = 1,52, Великобритании – D = 1,3, а для гладкого побережья Южной Африки D ≈ 1.

4.2. Массовая размерность

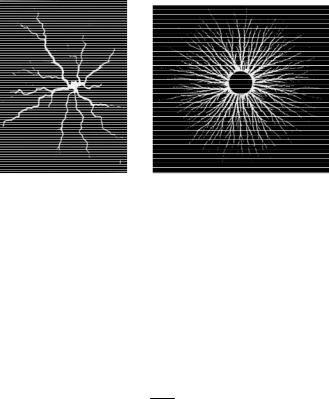
Во многих практически важных случаях удобно измерять так называемую массовую фрактальную размерность. Рассмотрим фигуру Лихтенберга – узор, образованный электрическим разрядом с металлического острия, размещенного на изоляторе (рис. 8).

а			б

Рис. 8

Измерение площади M светящейся области (или, что то же самое, массы вещества) внутри окружности радиусом R с центром на острие дает закон роста

M RD .

Однако D здесь не равен двум, как в случае сплошной однородной фигуры на плоскости. Для фигуры Лихтенберга D заключен в интервале от 1,7 (рис. 8,а) до 1,9 (рис. 8,б) и называется массовой фрактальной размерностью. При этом число каналов, пересекающих окружность, равно

N(R) = dMdR RD −1 .

14

Во всех случаях для фрактальных объектов увеличение «массы» внутри радиуса R определяется показателем, меньшим евклидовой размерности пространства вложения. Для регулярных математических фракталов массовая размерность совпадает с фрактальной размерностью.

4.3. Ограниченная диффузией агрегация (ОДА)

Процесс ОДА можно рассматривать как задачу, в которой частицы совершают случайное блуждание до тех пор, пока не достигнут поверхности кластера, на которой переходят в состояние покоя. Соответственно поверхность в точке присоединения частицы вырастает на один шаг. При этом возникают красивые случайные фракталы (рис. 9), напоминающие определенные модели биологического роста, роста кристаллов и фигуры Лихтенберга. Для таких фракталов характерна древовидная структура с многочисленными «фьордами». Причина образования подобных структур при ОДА заключается в том, что блуждающая частица оседает, как правило, вблизи выступа фрактала, а не в глубине «фьорда», поскольку вероятность проникновения туда, не «застряв» где-нибудь по пути,

Рис. 9

15

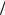
чрезвычайно мала. Компьютерное моделирование обнаруживает, что фрактальная размерность для двумерной ОДА лежит вблизи 1,7, для трехмерной – вблизи 2,5.

В континуальном пределе частицы, совершающие случайное блуждание, описываются уравнением диффузии

∂u(r , t)		G
∂t	= K u(r , t) ,
где u(r , t) – концентрация частиц,		K – коэффициент диффузии.
В стационарном состоянии ∂u(r , t)		∂t = 0 и уравнение диффузии
сводится к уравнению Лапласа	u(r , t) = 0 .
Локально гладкая граница движется			со	скоростью v =
= −K (nG u(rG, t))|S в направлении нормали			n,	перпендикулярной

поверхности.

Отсюда следует, что внешнее сходство между фигурами Лихтенберга, молниями, другими типами электрического разряда и формами ОДА не случайно, поскольку эти процессы описываются уравнением Лапласа, причем градиент потенциала соответствует полю диффузии в ОДА, а поверхность кластера ОДА – эквипотенциальной поверхности. При таком подходе можно предположить, что рост кластера наиболее вероятно будет происходить в направлении наибольшего градиента потенциала, т. е. вблизи выступов. Глубокие же «фьорды» хорошо заэкранированы и поэтому растут весьма слабо либо не растут вовсе.

4.4. Образование «вязких пальцев»

Образование вязких пальцев возникает вследствие гидродинамической неустойчивости поверхности раздела при вторжении жидкости или газа на территорию другой, более вязкой жидкости. Образование ветвистой фрактальной структуры (рис. 10, а – смешивающиеся; б – несмешивающиеся жидкости) качественно можно объяснить следующим. Любой «бугорок» на поверхности раздела имеет тенденцию к росту, поскольку у выступов градиент давления,

16

обуславливающий рост, достигает наибольшей величины. В случае несмешивающихся жидкостей, например, глицерина и нефти, пальцы гораздо шире, потому что поверхностное натяжение на границе раздела препятствует образованию тонких дендритов.

а

б

Рис. 10

Данный эффект проявляется, например, когда в нефтесодержащий пласт под большим давлением закачивают воду для вытеснения нефти из битуминозной породы – стандартный метод «выдавливания». Если бы граница раздела воды и нефти была гладкой (D = 2), то через скважину можно было бы извлечь большую часть нефти, прежде чем вода достигнет насоса. К сожалению, в данном случае D больше 2 и вода достигает насоса задолго до того, как из нефтеносного пласта будет откачана вся нефть. Существует, однако, возможность уменьшить фрактальную размерность вязких пальцев путем добавления в воду особых полимеров, увеличивающих ее вязкость.

4.5. Фрактальные временные ряды

Многие наблюдения природных процессов приводят к долговременным рядам измерений. Например, имеются длинные ряды

17

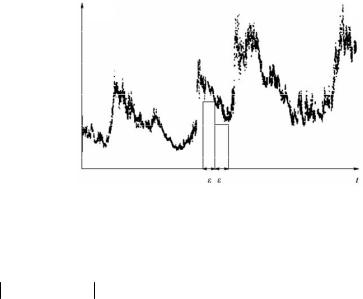
метеорологических измерений температуры воздуха, отложения ила, количества осадков, толщины колец деревьев, количества солнечных пятен и т. д. В отличие от детерминированных фракталов данные природные зависимости так или иначе связаны со стохастическими процессами и в этом смысле являются случайными. В качестве примера на рис. 11 представлена временная зависимость межпланетного магнитного поля.

B(t)

ε ε

t

Рис. 11

О таких рядах говорят как о статистически самоподобных фрактальных кривых. Аппроксимируя множество точек B(t) гистограммой с шагом ε, легко показать, что длина последней

∑ B(ti +ε) − B(ti ) расходится при ε→0 как ε−S . Из определения

i

(1) следует, что фрактальная размерность множества B(t) равна

D = 1 + S.

Для гладких кривых S = 0 и D = 1. Для непрерывной самоподобной кривой произвольного вида (0 ≤ S ≤ 1) фрактальная размерность заключена в пределах от 1 до 2.

Оказалось, что многие экспериментальные зависимости обладают фрактальной статистикой, анализ которой может быть проведен с помощью эмпирического анализа, предложенного Херстом. Всю свою жизнь Херст занимался изучением Нила и решением задач, связанных с накоплением водных ресурсов.

18

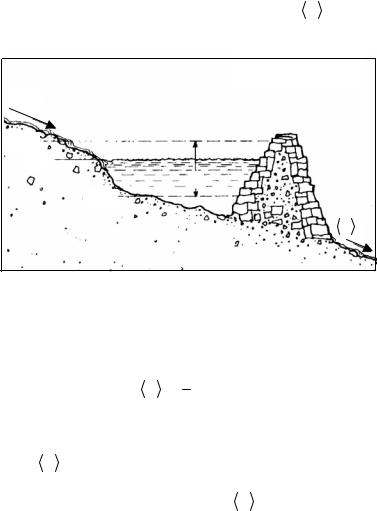
Проведем рассмотрение указанного подхода на примере задачи о нахождении оптимального объема водохранилища по заданному набору измерений притока воды. Оптимально то водохранилище, которое никогда не переполняется и не пустеет. В течение каждого года t такое водохранилище принимает приток воды B(t),

в то время как регулируемый объем воды (сток) B τ спускается из него (рис. 12).

B(t()t)

Xmax

X(t)

R

Xmin

B

B τ τ

Рис. 12

Сколько воды должно храниться в водохранилище, чтобы каждый год из него можно было спускать объем воды, равный среднему притоку за этот период? Средний приток за период τ лет равен

B τ = 1 ∑τ B(t) .

τt =1

Это среднее должно равняться объему, ежегодно спускаемому из водохранилища. Пусть X(t) – накопившееся отклонение B(t) от

среднего B τ :

t

X (t, τ) = ∑ (B(k) − B τ ).

k =1

19