
Планирование эксперимента и измерение физических величин
..pdf
|
|
|
|
Таблица |
2 . 4 |
|||
Переход от нелинейной зависимости к линейной |
|
|
||||||
|
|
|
|
|
|
|
||
Общий вид нелинейной |
Результирующая линейная |
y |
x |
a |
b |
|||
зависимости |
зависимость |
|
|
|
|
|||
ν = k uz |
ln ν = z ln u + ln k |
ln ν |
ln u |
z |
ln k |
|||
ν = k ezu |
ln ν = zu + ln k |
ln ν |
u |
z |
ln k |
|||
ν = k ez /u |
ln ν = zu−1 + ln k |
ln ν |
u−1 |
z |
ln k |
|||
ν = |
u |
|
u−1 |
ν−1 |
u−1 |
k |
z |
|
k + zu |
||||||||
|
|
|
|
|
|
|||
Во время определения погрешностей величин a и b для перехода к погрешностям реальных физических величин k и z необходимо применять формулы для расчета погрешностей косвенных измерений.
2.9. Метод наименьших квадратов
Данный метод часто используется для статистической обработки экспериментальных данных, которые определяются различными функциональными зависимостями физических величин друг от друга. Разумеется, этот метод можно применить и к линейной зависимости, что позволяет определить достоверные оценки ее параметров a и b и оценить их погрешности.
В качестве примера можно рассмотреть статистическую модель некого эксперимента, в котором исследуется линейная зависимость. Предположим, что проведено n > 2 парных измерений величин x и y: xi, yi, где i = 1, ..., n. Исходя из экспериментальных данных требуется определить оценки параметров a и b, а также оценки их дисперсий σ2a и σ2b. Сделаем следующие предположения относительно природы погрешностей:
1.Величины xi определены достоверно, т.е. без погреш-
ностей.
2.Величины yi распределены взаимно независимо, обладают одинаковой дисперсией σ2 и соответствуют нормальному закону
распределения. Распределения yi имеют средние значения yi , соответствующие точным значением функцииaxi + b.
81
Стр. 81 |
ЭБ ПНИПУ (elib.pstu.ru) |
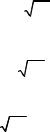
3. Систематические погрешности отсутствуют, т.е. все точки, выходящие за 3σ-интервал (промахи), отброшены.
Сформулируем функцию правдоподобия в виде вероятности реализации набора полученных экспериментальных данных:
l = |
|
1 |
|
|
|
( y1 − (ax1 |
+ b))2 |
||||
|
|
|
exp − |
2σ |
2 |
... |
|||||
σ |
2π |
||||||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
( yn − (axn + b))2 |
||||||
... |
|
|
|
exp − |
|
2σ |
2 |
= |
|||
σ |
2π |
|
|||||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
n |
|
1 |
|
n |
2 |
|
|
|
|
|||||||
= |
|
|
|
|
exp − |
|
|
( yi − (axi + b)) |
|
σ |
|
|
2σ |
2 |
|
||||
|
2π |
|
|
|
i=1 |
|
|||
Прологарифмировав обе части, имеем
.
ln L = − n ln 2π − n ln σ2 |
|
1 |
|
n |
|
− |
|
( yi − (axi + b))2 . |
|||
2σ |
2 |
||||
2 |
2 |
|
|
i=1 |
|
Логично в качестве оценок a, b, σ2 принять значения, для которых L и lnL будут максимальны, т.е. будет реализована наибольшая вероятность получения набора экспериментальных данных. Максимумдля функцииlnL определяют дифференцированием:
∂ ln L |
= 0, |
∂ ln L |
= 0, |
∂ ln L |
= 0 . |
|
∂a |
∂b |
∂σ2 |
||||
|
|
|
После операции дифференцирования система уравнений, разрешеннаяотносительно искомых параметров, будет иметьвид
|
n |
( y |
− ax |
− b) |
= 0, |
|
x |
||||
i |
i |
i |
|
|
|
i-1 |
|
|
|
|
|
|
n |
|
|
|
|
( yi − axi − b) = 0, |
|
||||
i-1 |
|
|
|
|
|
|
|
n |
|
|
|
nσ2 = ( yi − axi − b)2 . |
|||||
|
|
i-1 |
|
|
|
|
|
|
|
|
|
82
Стр. 82 |
ЭБ ПНИПУ (elib.pstu.ru) |
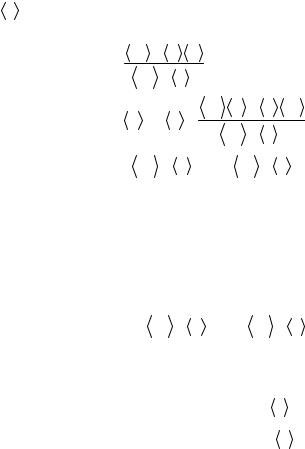
Определив среднюю величину каждого параметра как
z = 1 n zi , имеем n i=1
|
|
xy |
− x |
y |
|
|
|
|
|
|
|
a = |
x2 |
− x |
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
x2 |
y |
− x |
|
xy |
|
|
|
|
|
|
|
|
|
|||||
b = |
|
y − a x |
= |
|
x2 |
− |
x |
2 |
|
, |
|
|
|
|
|
|
|
|
|
|
|||
|
|
y2 |
− y 2 − a2 ( x2 |
− x 2 ). |
|||||||
σ2 |
= |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Для того чтобы оценки дисперсии оказались несмещенными относительно точного значения (из-за того, что число измерений конечно, полученные значения параметров a и b будут отличаться от предельных), последнее выражение в системе необходимо домножить на n/(n – 2):
σ2 = |
n |
|
y2 |
− |
y 2 − a2 ( x2 − |
x |
2 ) . |
(*) |
|
||||||||
|
n − 2 |
|
|
|
|
|
|
|
Теперь нужно оценить дисперсии параметров. Выражение для a преобразуем в виде
n |
xj − x |
|
|
|
a = k j y j , где k j = |
|
|
. |
|
n |
|
2 |
||
j=1 |
(xj − x |
) |
|
|
|
|
|
||
|
j=1 |
|
|
|
После процедуры преобразования становится видно, что a представляет собой линейную комбинацию независимых друг от друга величин yj, поскольку все коэффициенты kj определены точно. Значит, параметр a распределен по нормальному закону, а его дисперсия σ2a представляет собой линейную комбинацию дисперсий величин yj с коэффициентами kj2 (свойство сложения нормальных распределений упоминалось при рассмотрении погрешностей косвенных измерений):
83
Стр. 83 |
ЭБ ПНИПУ (elib.pstu.ru) |
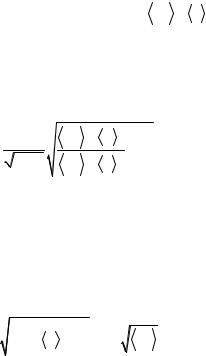
n |
|
|
|
nσ |
2 |
|
|
|
|
|
|
σ |
2 |
|
|
|
σ2a = k j |
2σ2 = |
|
|
|
|
|
|
= |
|
|
|
|
|
. |
||
n |
|
|
n |
|
2 |
n |
|
x2 − |
x |
2 |
||||||
j=1 |
|
|
|
|
( |
) |
|
|||||||||
|
|
n xi |
2 |
− |
xi |
|
|
|
|
|
|
|
||||
|
|
i=1 |
|
i=1 |
|
|
|
|
|
|
|
|
|
|
||
Подставив сюда выражение для определения дисперсии (*), выведем выражение для оценки стандартного отклонения параметра a:
σa = |
1 |
y2 |
− |
y |
2 |
− a2 . |
|
− |
x 2 |
||||
|
n − 2 x2 |
|
||||
Модифицируем выражение из системы для b:
|
1 |
n |
1 |
n |
b = |
yi − a |
xi . |
||
|
n |
i=1 |
n |
i=1 |
|
|
|
Этот параметр также распределен по нормальному закону. Стандартное отклонение для него
σb = |
σ2 |
+ x 2 σ2a = σa x2 . |
|
n |
|
При переходе от величин σa и σb к погрешностям a и b их необходимо домножить на коэффициент Стьюдента:
a= t (α, n − 1)σa ,
b= t (α, n − 1)σb ,
где α – уровень статистической значимости; n – количество парных измерений. Вычислять n – 1 необходимо потому, что в методе наименьших квадратов из экспериментальных данных определяют не одну величину, а две – a и b. Эта взаимосвязь уменьшает количество независимых случайных переменных, участвующих в распределении Стьюдента.
В случае когда линейная зависимость была получена из модельной методом линеаризации, переход к погрешностям реаль-
84
Стр. 84 |
ЭБ ПНИПУ (elib.pstu.ru) |

ных физических величин может быть осуществлен по формулам для определения погрешностей косвенных измерений. Затем результат записывается в окончательном виде.
Данный метод наилучшей линеаризации данных называется
методом наименьших квадратов, так как при таких параметрах достигается минимум величины «отклонения» прямой от экспериментальных данных:
S = n ( yi − (axi + b))2 .
i=1
В частном случае, когда предполагается, что теоретическая линейная зависимость проходит через начало координат (вид y = kx), для определения величины параметра k и его погрешности применяют следующие формулы:
k =  xxy2
xxy2  ,
,
σ2 = n −n 2 (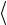 y2
y2 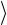 − k 2
− k 2 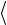 x2
x2 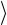 ),
),
σk = |
|
σ |
2 |
= |
1 |
|
y2 |
− k 2 . |
n( |
x2 − x 2 ) |
n − 2 |
|
x2 |
||||
|
|
|
|
|||||
Типичной ошибкой будет определение значения параметра k путем усреднения коэффициентов наклона различных точек, полученных в ходе эксперимента:
kусред = 1 n yi .
n i=1 xi
Это значение не будет являться оптимальным, так как точки, расположенные ближе к началу координат, будут вносить больший вклад, чем точки на другом конце графика, искажая тем самым результат.
85
Стр. 85 |
ЭБ ПНИПУ (elib.pstu.ru) |
Зачастую в процессе обработки линейной зависимости требуется определить координату точки пересечения графи-
ком оси x:
c = − ba .
Соответствующая дисперсия
2 |
2 |
|
σ2a |
|
σ2b |
|
||
σ c = c |
|
|
|
|
+ |
|
|
. |
|
a |
2 |
b |
2 |
||||
|
|
|
|
|
|
|
||
86
Стр. 86 |
ЭБ ПНИПУ (elib.pstu.ru) |
СПИСОК ЛИТЕРАТУРЫ
1.Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. – М.: Нау-
ка, 1976. – 254 с.
2.Афанасьева Н.Ю. Вычислительные и экспериментальные методы научного эксперимента: учеб. пособие для вузов. – М.:
КНОРУС, 2010. – 330 с.
3.Белов В.К. Метрологическая обработка результатов физического эксперимента: учеб. пособие для вузов. – 2-е изд. – Магнитогорск: Изд-во Магнитогор. гос. техн. ун-та им. Г.И. Но-
сова, 2000. – 116 с.
4.Волкова П.А., Шипунов А.Б. Статистическая обработка данных в учебно-исследовательских работах. – М.: ФОРУМ, 2012. – 96 с.
5.Гмурман В.Е. Теория вероятностей и математическая статистика: учеб. пособие для вузов. – 8-е изд., стер. – М.: Высш.
шк., 2002. – 479 с.
6.Гусейнов Ф.Г., Мамедяров О.С. Планирование эксперимента в задачах электроэнергетики. – М.: Энергоатомиздат, 1988. – 150 с.
7.Коваленко И.Н., Филиппова А.А. Теория вероятностей и математическая статистика: учеб. пособие для вузов. – М.:
Высш. шк., 1973. – 368 с.
8.Коробко В.И. Лекции по курсу «Основы научных исследований»: учеб. пособие для вузов. – М.: АСВ, 2000. – 217 с.
9.Лялькина Г.Б., Бердышев О.В. Математическая обработка результатов эксперимента: учеб. пособие для вузов. – Пермь: Изд-во Перм. нац. исслед. политехн. ун-та, 2013. – 77 с.
10.Математические методы планирования эксперимента. – Новосибирск: Наука, 1981.
11.Мелас В.Б. Общая теория функционального подхода к оптимальному планированию эксперимента: учеб. пособие. – СПб.: Изд-во С.-Петерб. гос. ун-та, 1999. – 67 с.
87
Стр. 87 |
ЭБ ПНИПУ (elib.pstu.ru) |
12.Назаров Н.Г. Измерения: планирование и обработка результатов. – М.: Изд-во стандартов, 2000. – 302 с.
13.Пен Р.З. Планирование эксперимента в Statgraphics. – Красноярск: Кларетианум, 2003. – 248 с.
14.Решетников М.Т. Планирование эксперимента и статистическая обработка данных: учеб. пособие. – Томск: Изд-во Том. гос. ун-та систем управления и радиоэлектроники ТГУСУиР, 2000. – 231 с.
15.Рогов В.А., Позняк Г.Г. Методика и практика технических экспериментов: учеб. пособие для вузов. – М.: Academia, 2005. – 283 с.
16.Сидняев Н.И. Теория планирования эксперимента и анализ статистических данных: учеб. пособие для вузов. – М.:
Юрайт, 2011. – 399 с.
17.Смирнов Н.Н., Федосов В.П., Цветков Ф.А. Измерение характеристик случайных процессов: учеб. пособие для вузов / под ред. В.П. Федосова. – М.: Сайнс-Пресс, 2004. – 64 с.
18.Соловьев В.П., Богатов Е.М. Организация эксперимента: учеб. пособие для вузов. – Старый Оскол: ТНТ, 2012. – 253 с.
19.Фаддеев М.А. Элементарная обработка результатов эксперимента: учеб. пособие для втузов. – СПб. [и др.]: Лань, 2008. – 117 с.
88
Стр. 88 |
ЭБ ПНИПУ (elib.pstu.ru) |

Учебное издание
А.В. Казаков
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА И ИЗМЕРЕНИЕ ФИЗИЧЕСКИХ ВЕЛИЧИН
Учебное пособие
Редактор и корректор И.А. Мангасарова
Подписано в печать 04.03.2014. Формат 60×90/16. Усл. печ. л. 5,75. Тираж 100 экз. Заказ 28/2014.
Издательство Пермского национального исследовательского
политехнического университета.
Адрес: 614990, г. Пермь, Комсомольский проспект, 29, к. 113.
Тел. (342) 219-80-33.
Стр. 89 |
ЭБ ПНИПУ (elib.pstu.ru) |
