m1008

Рис. 2.6. Схема сетевого графика для корректировки по трудовым ресурсам в масштабе времени

Из графика видно, что в первые три дня работы требуется 12 чел., а период с третьего по шестой день включительно уже для трех работ (1–2, 1–3 и 2–3) требуется 24 чел. Таким образом заполняют горизонтальную графу «До корректировки» и получают последовательно по периодам работ: 12, 24, 18, 22, 14, 6, 14, 8 чел. Оказалось, что график неоптимальный. Необходимо при сохранении общей трудоемкости выполнения каждой работы уменьшить число рабочих за счет сокращения численного состава бригад и увеличения продолжительности работы.

В горизонтальной графе «Условия корректировки с использованием резервов времени» показано, как это можно сделать:

1.Продлевая работу 1–3 на один день (за счет резерва времени), определяем требуемый численный состав бригады: 36 / 7 = 5 чел.

2.Продлевая работу 2–4 на три дня (за счет резерва времени), определяем требуемый численный состав бригады: 56 / 9 = 6 чел. Начало данной работы переносим на окончание работы 1–3.

3.Продлевая работу 5–6 на пять дней (за счет резерва времени), определяем требуемый численный состав бригады: 36 / 11 =

=3 чел.

21

После произведенных расчетов заполняем горизонтальную графу «После корректировки» и оцениваем оптимальность графика.

Корректировку сетевого графика по материалам можно производить на аналогично построенном графике. Методика расчета подобна применяемой при корректировке сетевого графика по трудовым ресурсам. Если лимитирующими являются несколько видов материалов, то задача значительно усложняется. В этом случае корректировать работы следует на вспомогательном линейном графике по каждому виду материала. Целесообразно корректировку сетевых графиков по материалам выполнять на вычислительной машине.

Корректировку по денежным средствам выполняют также на масштабном сетевом графике, придерживаясь изложенных выше принципов. График разделяют на участки, в пределах которых определяют суммарные сметные затраты, и сравнивают их с лимитом денежных средств, отпущенных для выполнения работ. Эти виды корректировок рассмотрены в учебнике [1].

3. Применение транспортной задачи линейного программирования при планировании организации строительства

Транспортная задача применяется для выбора оптимального варианта из множества возможных при решении задач планирования организации строительства и производства работ.

Задача сводится к составлению математической модели распределения какого-то вида продукции между ее поставщиками и потребителями и решению этой модели с целью нахождения такого варианта распределения, который давал бы минимум общих затрат по выбранному показателю. Такой вариант называют оптимальным, а минимум общих затрат – критерием оптимальности.

3.1. Постановка задачи

Имеется определенное число поставщиков продукции т, каждый из которых имеет свое количество продукции А, и ряд потребителей п с индивидуальным спросом Вj на эту продукцию.

22

Требуется прикрепить потребителей к поставщикам так, чтобы общий объем затрат по поставке продукции всем потребителям был наименьшим.

В качестве показателя критерия оптимальности Сij чаще всего принимается стоимость единицы продукции при доставке ее от поставщика i до потребителя j. Но может быть и другой показатель (например, дальность транспортирования, если себестоимость продукции у всех поставщиков одинакова).

Искомыми будут размеры перевозок Хij от поставщика i до потребителя j.

Для решения модели транспортной задачи должны быть удовлетворены следующие условия:

1. Объем поставок должен быть равен спросу потребителей (условие закрытой задачи):

m	i		n	j
	А			В	.
i 1			j 1

(3.1)

2. Показатели критерия оптимальности и размеры перевозок не могут быть отрицательными величинами, т.е.

C		0;
ij
X	ij	0.

(3.2)

(3.3)

3. Продукция каждого поставщика должна быть распределена между потребителями. Соответственно спрос каждого потребителя должен быть удовлетворен, т.е.

n
Ai X ij ;	(3.4)
j 1
m
B j X ij .	(3.5)

i 1

Проанализируем исходные данные. Уравнений (3.4) будет столько, сколько поставщиков, т.е. т, а уравнений (3.5) соответственно n.

В соответствии с равенством (3.1) общее число уравнений будет (т + п – 1). Таким образом, мы имеем систему уравнений, в которой число уравнений меньше, чем число неизвестных. Сле-

23

довательно, задача не имеет однозначного решения, она носит экстремальный характер.

Нужное нам оптимальное решение сводится к поиску целевой функции:

m n	ij	ij
			min,
	C X
i 1 j 1

(3.6)

что соответствует существу решаемой задачи.

3.2. Решение задачи

Последовательность действий при решении задачи рассмотрим на конкретном примере. По заданным или предварительно определяемым значениям Ai, Bi и Cij составляется матрица (табл. 3.1).

								Таблица 3.1
		Решение транспортной задачи
Поставщики и их					Потребители и их спрос, усл. ед.
мощность, усл. ед.				В1 = 500		В2 = 300	В3 = 400	Вф = 300
А1	= 400		2			3	1	0
А2	= 300		4			5	2	0
А3	= 300		6			4	3	0
А4	= 500		5			6	5	0

В левом верхнем углу каждой клетки матрицы записаны значения показателей критерия оптимальности для соответствующей пары поставщик – потребитель.

До составления матрицы необходимо проверить исходные данные задачи на выполнение условия (3.1). В данном случае это

условие не выполняется, так как

m	i
	A
1

1

500

, а

n B j

1

1

200

.

Чтобы это условие выполнялось, т.е. чтобы задача была закрытой, вводится фиктивный потребитель Вф, спрос которого ра-

m	n
вен разности Ai и	B j , т.е. Вф = 300 ед. Показатель критерия
1	1

оптимальности для фиктивного потребителя зависит от конкретной задачи. В данном случае он условно принят равным нулю,

24

т.е. на непоставляемую продукцию затрат нет. Таким образом, в первоначальной матрице появился последний столбец (выделен жирными линиями).

Методов решения транспортной задачи создано много. Приводим один из них, который называют методом коэффициентов. Алгоритм решения этим методом заключается в следующем:

1. Определение первоначального (базисного) распределения поставок, которое удовлетворяло бы условиям (3.1), (3.4) и (3.5). Наиболее просто это сделать способом северо-западного угла: удовлетворяя спрос потребителя, указанный в левом верхнем углу, постепенно сравнивая мощности поставщиков и спрос потребителей, распределяют поставки до правого нижнего угла.

В данном примере, сравнивая поставку А1 = 400 и спрос В1 = 500, отдаем всю поставку потребителю В1. Недостающие 100 ед. потребителю В1 берем у А2. Оставшиеся 200 ед. от А2 ставим потребителю В2 и т.д.

Полученное распределение вполне допустимо, так как оно удовлетворяет всем исходным условиям задачи. Но будет ли оно оптимальным? Будет ли суммарная стоимость обеспечения продукцией поставщиков

m n

S1 = XijCij = 400 2 + 100 4 + 200 5 + 100 4 + 200 3 +

i 1 j 1

+ 200 5 + 300 0 = 4 200

минимальной из всех возможных вариантов распределения, неизвестно.

2. Проверка оптимальности распределения. При решении методом коэффициентов необходимо, чтобы было выполнено следующее правило: количество клеток с поставками должно быть равно (m + п – 1). В нашем базисном распределении это условие выполнено, т.е. клеток с поставками (в табл. 3.2 показатели критерия оптимальности обозначены числом в скобках) оказывается семь. В случае если это условие не выполняется, можно увеличивать число клеток с поставками введением в свободную от поставки клетку условной нулевой поставки. Она никак не влияет на общее распределение, но дает возможность обеспечить количе-

25

ство клеток с поставками (т + п – 1). При этом не должна получиться замкнутая цепь.

					Таблица 3.2
Распределение поставок методом северо-западного угла
Поставщики и их		Потребители и их спрос, усл. ед.					Кстр
мощность, усл. ед.		В1 = 500	В2 = 300	В3 = 400	Вф = 300
А1 = 400	(2)		3	1	0		0
		400
А2 = 300	(4)		(5)	2	0		2
		100	200
А3 = 300	6		(4)	(3)	0		1
			100	200
А4 = 500	5		6	(5)	(0)		3
				200	300
Кстб		2	3	2	–3		–

Выполнив указанное условие, находим коэффициенты строк Кстр и столбцов Кстб. Первый коэффициент какой-либо строки или столбца задают любой величины, остальные считают, используя клетки с поставками, по условию

Кстр + Кстб = Cij.

В нашем примере задаем коэффициент первой строки Кстр равным нулю. Тогда, используя клетку А1В1, можем найти коэффициент первого столбца

Кстб1 = С11 – Кстр1 = 2 – 0 = 2.

Затем, используя клетку А2В1, находим коэффициент второй строки

Кстр2 = С11 – Кстолб 1 = 4 – 2 = 2.

Затем по клетке А2В2 находим Кстб2 и т.д.

Определив коэффициенты, считаем характеристики клеток без поставок. Характеристика клетки – это разность между показателем критерия оптимальности и суммой коэффициентов строки и столбца.

Подсчет характеристик приведен в табл. 3.3.

Таблица 3.3

Характеристики незаполненных клеток в табл. 3.2

Клетка	Cij	К	Cij – К
А1В2	3	3	0
А1В3	1	2	–1
А1Вф	0	–3	3

26

Клетка

А2В3

А2Вф

А3В1

А3Вф

А4В1

А4В2

В таблице

К

		Окончание табл. 3.3
Cij	К	Cij – К
2	4	–2
0	–1	1
6	3	3
0	–2	2
5	5	0
6	6	0

– это сумма коэффициентов строки и столб-

ца, соответствующих данной клетке.

Распределение поставок оптимально лишь тогда, когда все характеристики (см. табл. 3.3) будут положительными или равными нулю.

Следовательно, наше первое распределение не оптимально, так как две характеристики клеток А1В3 и А2В3 имеют отрицательные значения.

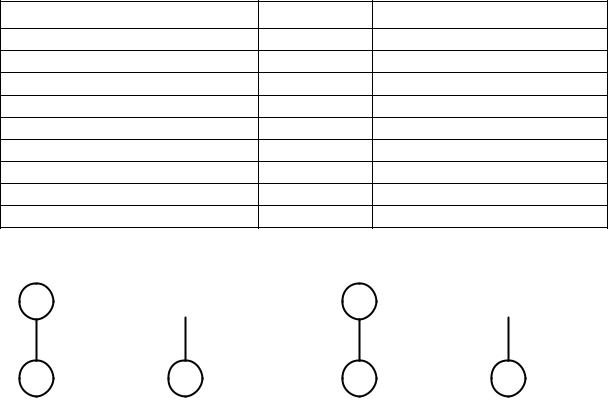
3. Улучшение первоначального распределения. Для этого выбираем клетку с отрицательной характеристикой, наибольшей по абсолютной величине. На схеме (рис. 3.1, а) выделим ее прямоугольником (клетка А2В3). Для этой клетки строится цепь перераспределения поставок. Цепь представляет собой замкнутый многоугольник с прямыми углами и четным количеством вершин. При этом одной из вершин многоугольника является клетка, для которой строится цепь, а остальные вершины – клетки, заполненные поставкой. Для данной клетки может быть только одна цепь. В вершинах цепи напишем величины поставок. Знаки вершин чередуются, начиная со знака плюс на клетке, для которой построена цепь. Наименьшее число сторон многоугольника – четыре, наибольшее (m + п). Так, для клетки А2В3 будет построена цепь, включающая клетки А2В2, А3В2 и А3В3 (см. рис. 3.1, а).

27

а)						б)
А	2	В	А	2	В	А	2	В	А	2	В
		2			3			2			3
–200			+						+

+100

–200

300

0

А	3	В	А	3	В	А	3	В	А	3	В
		2			3			2			3
Рис. 3.1. Схема цепи для клетки А2В3						до передвижки (а) и после нее (б)

Перераспределение поставок по цепи производится следующим образом. При отрицательных вершинах выбирается наименьшая поставка и передвигается по цепи. Передвижка (перераспределение) поставок осуществляется таким образом, чтобы их размеры увеличивались в клетках с положительным знаком и уменьшались в клетках с отрицательным. В этой цепи (см. рис. 3.1, а) передвижке подлежит поставка, равная 200. В данном случае в двух клетках А2В2 и А3В3 после вычитания передвигаемой величины оказываются нули. Для того чтобы количество клеток с поставками оставалось после перераспределения равным т + п – 1 = 7, в одной из этих клеток оставляем нулевую поставку. Следует помнить, что в процессе решения матрицы значение поставки, равное нулю, требует с собой такого же обращения, как и любое другое число. Таким образом, после передвижки поставки получается цепь, показанная на рис. 3.1, б, которую и записываем в матрицу (табл. 3.4).

Таблица 3.4

Распределение поставок после передвижки, выполненной для клетки А2В3

Поставщики и их		Потребители и их спрос, усл. ед.				Кстр
мощность, усл. ед.		В1 = 500	В2 = 300	В3 = 400	Вф = 300
А1 = 400	(2)		3	1	0	0
		400
А2 = 300	(4)		5	(2)	0	2
		100		200
А3 = 300	6		(4)	(3)	0	3
			300	0
А4 = 500	5		6	(5)	(0)	5
				200	300
Кстб		2	1	0	–5	–

28

Суммарные затраты при этом варианте составят S2 = 400 ∙ 2 +

+ 100 ∙ 4 + 200 ∙ 2 + 300 ∙ 4 + 0 ∙ 3 + 200 ∙ 5 + 300 ∙ 0 = 3 800, т.е. на 400

меньше, чем при первом варианте.

4. Проверка нового распределения на оптимальность (см. табл. 3.4) по известной уже методике.

В табл. 3.5 приведен расчет характеристик нового распределения. Как видно из этой таблицы, в клетке А4В1 имеется отрицательная характеристика. Следовательно, распределение не оптимально. Строим цепь для этой клетки. Она будет включать клетки А2В1, А2В3 и А4В3. Выполняем перераспределение, как и в первом случае (рис. 3.2, а).

Таблица 3.5

Характеристики незаполненных клеток в табл. 3.4

Клетка	Cij
А1В2	3
А1В3	1
А1Вф	0
А2В2	5
А2Вф	0
А3В1	6
А3Вф	0
А4В1	5
А4В2	6

К

1

0

–5

3

–3

3

–2

7

6

Cij – К

2

1

5

2

3

1

2

–2

0

а)	А 2В1		А 2В3	б)	А 2В1		А 2В3
	–100		+200				300

+		–200	100		100
А 4В1		А 4В3	А 4В1		А 4В3

Рис. 3.2. Схема цепи для клетки А4В1 до передвижки (а) и после нее (б)

Передвигаем по цепи поставку в 100 ед. Новое распределение приведено в табл. 3.6. Суммарные затраты при этом варианте со-

ставят S3 = 400 ∙ 2 + 300 ∙ 2 + 300 ∙ 4 + 100 ∙ 5 + 100 ∙ 5 = 3 600, т.е.

на 200 меньше.

29

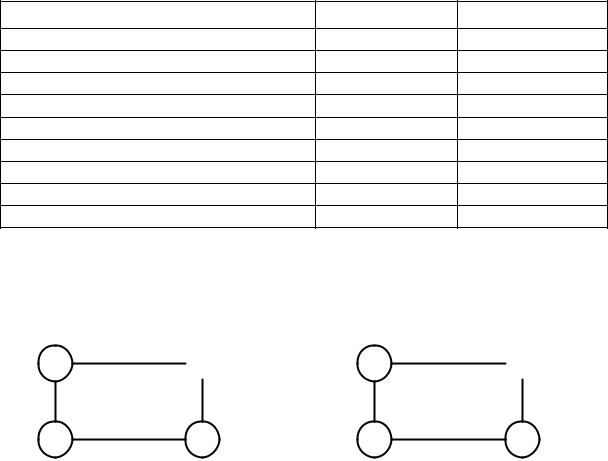
Таблица 3.6

Распределение поставок после передвижки, выполненной для клетки А4В1

Поставщики и их		Потребители и их спрос, усл. ед.				Кстр
мощность, усл. ед.		В1 = 500	В2 = 300	В3 = 400	Вф = 300
А1 = 400	(2)		3	1	0	0
		400
А2 = 300	4		5	(2)	0	0
				300
А3 = 300	6		(4)	(3)	0	1
			300	0
А4 = 500	(5)		6	(5)	(0)	3
		100		100	300
Кстб		2	3	2	–3	–

Подсчитав характеристики для распределения в табл. 3.6, видим, что в клетке А1В3 снова отрицательное значение (табл. 3.7).

Таблица 3.7

Характеристики незаполненных клеток в табл. 3.6

Клетка	Cij
А1В2	3
А1В3	1
А1Вф	0
А2В1	4
А2В2	5
А2Вф	0
А3В1	6
А3Вф	0
А4В2	6

К

1

0

–5

2

3

–3

3

–2

6

Cij – К

2

1

5

2

2

3

1

2

0

Составляем цепь для клетки А1В3 (рис. 3.3, а) и передвигаем поставку в размере 100 ед. (рис. 3.3, б).

а)						б)
А	1	В	А	1	В	А	1	В	А	В
		1			3			1		2	3
–400			+			300			100

+100

–100

100

А	4	В	А	4	В	А	4	В	А	4	В
		1			3			1			3

Рис. 3.3. Схема цепи для клетки А1В3 до передвижки (а) и после нее (б)

30