1383

В предлагаемой математической модели используются универсальные аппроксимациифункционалов В.Г. Зубчанинова [2]:

					σ(s) = Ф(s, ϑ10 , κ1 ) = Ф(s) + Af0p Ω − B sκ1,
	dσ			dФ			dΩ	(2)
			=			+ Af0p		− B	d	( sκ1 ), M1 = 2Gр + (2G − 2G0р ) f q ,
	ds						ds
				ds					ds
где				s	– приращение дуги траектории деформирования после

точки ее излома K с длиной дуги sKт , s = s − sKт ; Ф(s) – функция, описывающая единую кривую Одквиста – Ильюшина для процессов, близких к простым; Ω, f – функции сложного на-

гружения:

Ω (

s) = −

− γ s

+ b(1− e

−γ s

1− cosϑ1

γ

s e

)

; f

= f (ϑ1) =

2

(3)

Первая их них учитывает обобщенный эффект Баушингера как изменение длины вектора напряжений в виде «нырка» при сложной разгрузке и последующем вторичном пластическом деформировании, а вторая – направление вектора напряжений σ в процессе деформирования. Материальные параметры A, B, b, γ, p, q определяются экспериментально по соответ-

ствующей методике [1].

Уравнения модели (1) с конкретизированными функционалами (2, 3) приводятся к задаче Коши для определения компонент вектора σ и угла сближения ϑ1 , удовлетворяющих заданным на-

чальным условиям. Для поиска решения системы дифференциальных уравнений (1) использовался метод Рунге–Кутты четвертого порядка, реализованный в разработанном приложении на основе программного комплекса MathWorks MATLAB.

Оценка достоверности расчетных результатов по предлагаемой математической модели дается при сравнении расчетных

101

и опытных данных. Для этого на испытательном комплексе СН-ЭВМ имени А.А. Ильюшина в лаборатории механических испытаний кафедры «Сопротивление материалов, теории упругости и пластичности» ТвГТУ выполнены натурные экспериментальные исследования на трубчатых образцах из стали 45 в плоскости Э1 − Э3 векторного пространства деформаций при непро-

порциональном воздействии осевой силы и крутящего момента. В серии проведенных испытаний реализованные в опытах криволинейные траектории типа «центральная окружность» имели различную постоянную кривизну [3, 4]. Одна из таких двузвенных сложных траекторий с длиной первого звена и радиусом второго

R = 1,25 % = 0,0125, кривизной κ1 = 1/R = 80 и		углом излома
ϑ0	= 90 представлена на рис. 1.
1
	Отклик в пространстве напряжений S 1−S3	на реализован-

ную траекторию деформирования представлен на рис. 2. Диаграммы σ− s и ϑ1 − s , определяющие соответственно скаляр-

ные и векторные свойства материала, приведены на рис. 3, 4. Экспериментальные данные на рис. 1–4 представлены затушеванными кружочками.

Расчетные кривые 1 на рис. 2–4 получены при учете в функционалах процесса всех параметров внутренней геомет-

рии плоской траектории s, κ1, ϑ10 и обобщенного эффекта Бау-

шингера, реализуемого на нырке напряжений при сложной неупругой разгрузке. Как видно, расчетные результаты достаточно хорошо соответствуют эксперименту. Расчетные кривые 2 на рис. 2–4 получены без учета кривизны в аппроксимациях функционалов (2) при параметре B = 0 , что соответствует процессам деформирования типа кусочно-ломаных прямолинейных траекторий, в том числе с излома более 90 град [5]. Расчетные кривые 3 получены с учетом кривизны в аппроксимациях функционалов (2) при B ≠ 0 , но при A = 0 , что соответствует гладкой

102

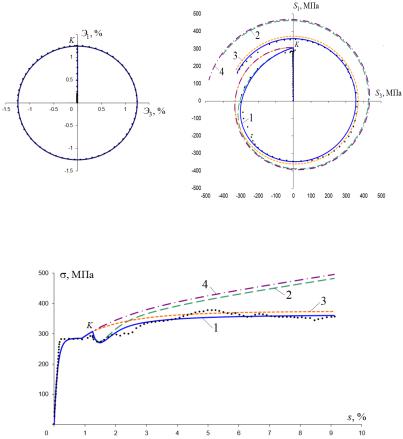
траектории без угла излома и неизбежно приведет к заметному отклонению от эксперимента в окрестности точки излома при углах более 90 град. Расчетные кривые 4 соответствует модельному представлению теории течения Прандтля–Рейса–Хилла для материалов с упрочнением, но без учета эффекта Баушингера [6]. Здесь было принято M1 = 2G и закон упрочнения Одкви-

ста–Ильюшина σ = Ф(s) .

Рис. 1. Двузвенная сложная	Рис. 2. Отклик на реализованную
траектория	траекторию деформирования

Рис. 3. Диаграмма σ− s

103

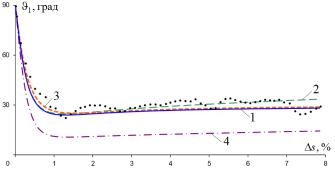
Рис. 4. Диаграмма ϑ1 − s

Предлагаемая математическая модель для рассмотренной траектории дала расчетные результаты (кривые 1 на рис. 2–4), хорошо соответствующие эксперименту, что также подтверждается на траекториях из данной серии экспериментов с другими постоянными кривизнами [3, 4]. Пренебрежение параметрами

кривизны κ1 или углами излома ϑ10 в аппроксимациях функционалов дает заметное расхождение с опытными данными.

Список литературы

1.Ильюшин А.А. Пластичность. Основы общей математической теории. – М.: Изд-во АН СССР, 1963. − 271 с.

2.Зубчанинов В.Г. Механика процессов пластических сред. – М.: Физматлит, 2010. − 352 с.

3.Алексеев А.А., Зубчанинов В.Г. Численное исследование процессов сложного упругопластического деформирования стали по криволинейным траекториям // Математическое моделирование в естественных науках. – 2015. – Т. 1. – С. 8–12.

4.Зубчанинов В.Г., Алексеев А.А., Гультяев В.И. Численное моделирование и построение образа процесса упругопластического деформирования стали по сложным плоским окружным траекториям // Вестник Чуваш. гос. пед. ун-та

104

им. И.Я. Яковлева. Сер. Механика предельного состояния. – 2015. – № 4 (26). – С. 39–49.

5.Зубчанинов В.Г., Алексеев А.А. Применение модифицированной модели теории процессов к расчетам упругопластического деформирования стали по ломаным траекториям // Успехи механики сплошных сред: сб. докл. междунар. конф., приуроч.

к75-летию акад. В.А. Левина. – Чебоксары, 2014. – С. 200–203.

6.Zubchaninov V.G., Alekseev A.A., Alekseeva E.G. Mathematical modeling of plastic deformation of materials on complex flat trajectories // Materials Physics and Mechanics (MPM). – 2015. – No. 2, vol. 24. – Р. 107–118.

СЛАБОНЕЛИНЕЙНЫЙ АНАЛИЗ ДЛИННОВОЛНОВОЙ КОЛЕБАТЕЛЬНОЙ КОНВЕКЦИИ МАРАНГОНИ

В СЛОЕ БИНАРНОЙ СМЕСИ

А.О. Иванцов

Институт механики сплошных сред УрО РАН,

Пермь, Россия, [e-mail]

Проведен анализ устойчивости длинноволновой термо- и кон- центрационно-капиллярной конвекции в слое бинарной смеси. Получены нелокальные нелинейные амплитудные уравнения, описывающие развитие длинноволновой колебательной неустойчивости. Определены условия устойчивости конечно-амплитудных структур.

Ключевые слова: тонкие пленки; длинноволновая колебательная неустойчивость; слабонелинейный анализ; отбор структур.

Рассмотрим тонкий слой бинарной жидкости толщиной d. На нижней границе слоя, z = 0 , поддерживается постоянный поток тепла. Такая ситуация реализуется в случае, если теплопроводность подложки много меньше теплопроводности жидкости. При отсутствии движения жидкости в слое создается вертикальный градиент температуры, который, в свою очередь, бла-

105

годаря эффекту термодиффузии создает градиент концентрации. Верхняя свободная граница жидкости предполагается недеформируемой, при этом поверхностное натяжение зависит как от температуры, так и от концентрации:

σ = σ0 − σT (T − T0 ) + σC (C − C0 ).

Выбирая в качестве единиц измерения времени, длины, температуры, концентрации примеси, скорости и давления следующие величины: d 2 / κ, d , ad , adσT / σC , κ / d , ρνκ / d 2 (где

κ, ρ, ν – температуропроводность, плотность и кинематическая

вязкость жидкости), получим следующую систему уравнений и граничных условий:

v = 0,

P−1 (vt + v v) = − p + 2 v,

Tt + v T = 2T,

L−1 (Ct + v C ) = 2 (C + χT ),

z = 0 : v = 0,	Tz + 1 = (C + χT )z = 0,
z = 1: w = Tz + BT = (C + χT )z = 0,
uz = −M 2 (T − C ).
Здесь v = u + wez , 2 –	двухмерная проекция градиента

на плоскость (x, y) . Здесь и далее индексами обозначены част-

ные производные по соответствующим координатам. Задача содержит следующие безразмерные параметры:

M =	σT ad 2	, B =	qd	, χ =	ασC	, P =	ν	, L =	D	.
	ρνκ		kth		σT		κ		κ

106

Это число Марангони, число Био, число Соре, число Прандтля и число Льюиса. Здесь q, kth , α – соответственно коэффици-

ент теплоотдачи от поверхности жидкости к окружающей среде, теплопроводность и коэффициент Соре. Также может быть введено число Шмидта S = P / L .

Краевая задача имеет простое решение в случае, когда жидкость покоится:

T0 = 1+ B − z, C0 = const + χz, v0 = 0.

B

Линейная устойчивость данного положения равновесия была исследована в работе [1] для случая k ~ B1/4 (рисунок).

В работе [1] были получены граница длинноволновой колебательной неустойчивости и аналитическая формула для длинноволновой монотонной моды неустойчивости:

M0(0) = 48m0(0) = 48	L	,	χL = χ + L + χL.
	χL
В частности, было показано,			что при χ < χm∞ = −L / (1+ L)

неустойчивость имеет место при отрицательных числах Марангони, т.е. при нагреве сверху.

В работе [2] рассмотрен случай k ~ B и показано, что такое приближение расширяет область параметров, в которой наблюдается развитие длинноволновой монотонной неустойчивости (см. рисунок):

L(k2 + B)

M* = 48m0(B) = 48 χL k2 + χB .

Слабонелинейный анализ этой моды проведен в [3]. Рассмотрим нелинейную эволюцию длинноволновых воз-

мущений масштаба O(B−1/2 ) . Возмущения температуры и кон-

107

центрации предполагаются конечными, в то время как возмущения скорости – малыми. При этом продольные компоненты скорости много больше вертикальной компоненты.

M c

0

χo∞	χ	χm∞ 0

Рис. Карта линейной устойчивости слоя бинарной жидкости. Сплошная линия – граница монотонной неустойчивости, полученной в [1], штрихпунктирная линия – новая мода монотонной неустойчивости [2], пунктирная линия – колебательная неустойчивость

Условие разрешимости задачи второго порядка приводит к уравнениям для амплитудных функций. Анализ полученных амплитудных уравнений позволяет предсказать режим конвекции вблизи порога устойчивости. Показано, что для структур на квадратной решетке отбираются чередующиеся валы, которые являются устойчивыми и по отношению к внешним возмущениям с произвольным волновым вектором, не принадлежащим квадратной решетке.

Для волновых прямоугольных режимов ситуация более сложная. В этом случае также устойчивы чередующиеся валы на прямоугольной решетке: суперпозиция двух стоячих волн с разностью фаз в девяносто градусов, поляризованных под углом друг к другу. Однопараметрическое семейство (в качестве параметра выступает угол между базисными векторами решетки) чередующихся валов на прямоугольной решетке яв-

108

ляется устойчивым по отношению к внешним возмущениям, если угол между базисными волновыми векторами превышает 60 град. Следует также отметить, что чередующиеся валы на квадратной решетке не являются предельным случаем чередующихся валов на прямоугольной решетке в силу того, что для квадратов возникают дополнительные резонансы и важна генерация «наклонных волн».

Для структур на гексагональной решетке в системе с кубической нелинейностью отбирается целое трехпараметрическое семейство решений. Отбираются либо волновые валы (wavy rolls; валы, искривленные в продольном направлении подобно гармонической волне), либо в системе вообще нет устойчивых решений, и реализуется гетероклинический цикл: система блуждает между тремя неустойчивыми предельными циклами, поочередно притягиваясь и отталкиваясь от каждого из них. Исследована также устойчивость гексагональных структур относительно внешних возмущений.

Работа выполнена при финансовой поддержке из средств гранта РФФИ 14-01-00148.

Список литературы

1.Oron A., Nepomnyashchy A.A. Long-wavelength thermocapillary instability with the Soret effect // Phys. Rev. E. – 2004. – Vol. 69. – 016313.

2.Podolny A., Oron A., Nepomnyashchy A.A. Long-wave Marangoni instability in a binary-liquid layer with deformable interface in the presence of Soret effect: Linear theory // Phys. Fluids. – 2005. – Vol. 17. – 104104.

3.Шкляев С.В., Иванцов А.О. Исследование амплитудных уравнений длинноволновой конвекции марангони в слое бинарной смеси // Вестник Перм. ун-та. Сер. Физика. – 2016. –

№1 (32). – С. 55–63.

109

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА ОСАДКИ ЦИЛИНДРИЧЕСКОЙ ЗАГОТОВКИ

Ю.А. Казаринова, Т.Е. Мельникова

Пермский национальный исследовательский политехнический университет,

Пермь, Россия, [e-mail], [e-mail]

Рассматривается численный эксперимент процесса осадки цилиндрической заготовки в программном комплексе QForm 2D/3D, позволяющий определять рациональные параметры процесса и оценить устойчивость формы при деформировании с целью получения качественных изделий. Исследуются особенности процессов деформирования при осадке заготовок, связанные с физическими характеристиками материала, масштабным фактором заготовок, видами оборудования и технологическими параметрами процесса.

Ключевые слова: численное моделирование, пластическая деформация, осадка, напряженное состояние, рациональная технология, устойчивость, качество.

Основой многих прогрессивных ресурсосберегающих технологий является обработка металлов давлением, среди известных методов которой наиболее эффективным является осадка, позволяющая значительно экономить материал при производстве поковок [1–3]. Повышение эффективности технологии обработки металлов давлением является актуальной задачей. С точки зрения экономичности при разработке оптимальной технологии обработки металлов давлением преимущество имеет программная реализация численных методов [4].

Задачи производства, связанные с минимизацией затрат на освоение и отладку новых технологий, усовершенствование и оптимизацию форм рабочего инструмента и заготовки, успешно решаются путем применения математического моделирования процессов обработки металлов давлением.

В этом плане большое значение имеет реализация численных экспериментов процесса осадки в программном пакете QForm 2D/3D, который является комплексом инжинирингового программного обеспечения для разработки, анализа и оптимиза-

110