2937

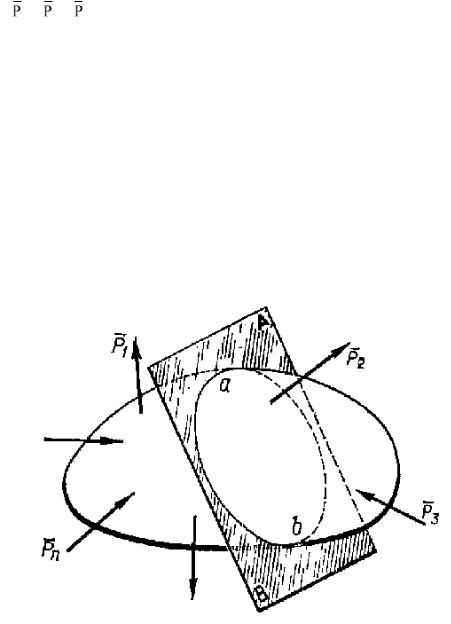
Одной из основных задач расчетов на прочность является выяснение характера и величины внутренних сил упругости, действующих в нагруженной детали. Для этого используется метод сечений, заключающийся в следующем. Мысленно проведем сечение тела, на которое

действуют силы 1, 2, 3 и т.д. (рис.4.1,а), плоскостью АВ. Поскольку тело под действием указанных сил находится в равновесии, то в равновесии находится любая его часть, расположенная по одну сторону от сечения. Отбросим мысленно правую часть и рассмотрим условия равновесия оставшейся левой части. Для того чтобы оставшаяся часть находилась в равновесии, на поверхности сечения должны действовать силы, эквивалентные действию правой части на левую. Такими силами являются внутренние силы упругости, распределенные по сечению ab. Следовательно, с помощью метода сечений внутренние силы упругости переводятся в разряд внешних сил и для их отыскания оказывается возможным применить соответствующие теоремы статики.

а)

31

б)

Рис. 4.1. К методу сечений

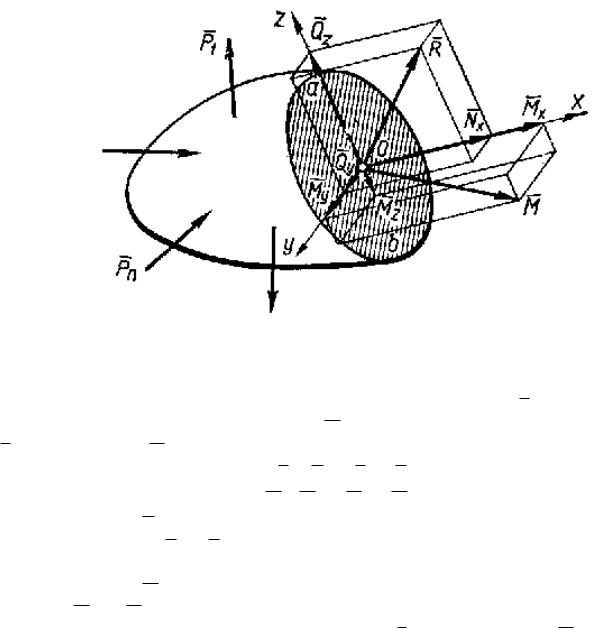
Система внутренних сил упругости может быть сведена к одной силе R (главному вектору

внутренних сил упругости) и одному моменту M (главному моменту этих сил). Главный вектор

R и главный момент M разложим на составляющие по осям координат (рис. 4.1,б):

R = N x + Q y + Q z; M = M x + M y + M z.

Составляющая N x, называемая нормальной силой, вызывает деформацию растяжения или

сжатия. Составляющие Q y и Q z, стремящиеся сдвинуть одну часть тела относительно другой, называют поперечными силами.

Составляющая M х главного момента скручивает тело и называется крутящим моментом.

Моменты M y и M z изгибают тело соответственно в плоскостях xOz и xOy и называются

изгибающими моментами. Отыскание главного вектора R и главного момента M внутренних сил упругости (либо их составляющих) составляет одну из основных задач расчета на прочность. Если внешние силы заданы, то усилия Nx, Qy, Qz и моменты Мx, Мy, Мz вычисляются на основании уравнений равновесия как алгебраические суммы проекций и моментов внешних сил, действующих на одну из частей рассеченного тела.

Интенсивность внутренних сил упругости называется напряжением и измеряется в единицах механического напряжения (Паскаль, Па). Напряжение зависит от ориентации сечения, проведенного через данную точку. Ориентация сечения определяется направлением внешней нормали к нему.

32

Рис. 4.2. Полное напряжение и его составляющие

Рассмотрим в деформированном теле произвольное сечение с нормалью n (рис.4.2).

Выделим около точки М малую площадку

F. Если равнодействующая сил упругости,

действующих по этой площадке, будет

P , то полное напряжение p n в точке М по площадке с

нормалью n:

P

.

p n = lim

F

0

F

Это напряжение

принято раскладывать

на две составляющие – нормальную

n и

тангециальную (касательную) n.

Поскольку

n =

n +

n , то:

pn =

2n

2 n.

В свою очередь,

нормальное напряжение

n

можно разложить по осям координат на

составляющие

nx,

ny,

nz . Аналогично можно получить составляющие касательного

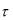напряжения nx, ny, nz.

4.2. Центральное растяжение (сжатие) прямого бруса

Брусья и стержни. Деформацию растяжения (сжатия) исследуют на брусьях или стержнях телах, отличающихся тем, что у них один размер значительно больше двух других. В зависимости от геометрической оси различают прямолинейные и криволинейные брусья. Стержнем обычно называют тонкий и длинный брус с прямолинейной осью. Размеры и форма поперечных сечений могут быть постоянными или переменными.

Растяжение стержня происходит, когда к его концам приложены силы, направленные вдоль его оси. Выводы, относящиеся к деформации центрального растяжения, чаще всего применимы и к центральному сжатию. Существенные различия этих деформаций наблюдаются

33

при изучении разрушения материалов, а также при исследовании поведения весьма длинных и тонких стержней, для которых сжатие сопровождается, как правило, выпучиванием.

а)

б)

Рис. 4.3. К гипотезе плоских сечений

Закон Гука. Исследуем сначала случай, когда прямолинейный брус постоянного поперечного сечения площадью F растягивается равномерно распределенными нагрузками интенсивности q, приложенными на его торцах параллельно геометрической оси (рис.4.3,а) .

Равнодействующие распределенных усилий P = qF будут направлены параллельно геометрической оси и приложены в центрах тяжести торцевых сечений. Для такой деформации брусьев практикой подтверждается гипотеза плоских сечений - гипотеза Бернулли, в соответствие с которой сечения, бывшие плоскими до деформации, останутся плоскими и после деформации; поперечные сечения а - а, b - b, ..., m - m после деформации лишь сместятся поступательно друг относительно друга. В связи с этим можно предположить, что внутренние силы упругости будут распределены равномерно по любому плоскому сечению (напряжение x = const).

Рассмотрим равновесие части стержня, лежащей слева от сечения m - m (рис.4.3,б). На выделенную часть по сечению m - m действуют внутренние силы упругости, имеющие равнодействующей нормальную силу N, а также равномерно распределенная нагрузка (с интенсивностью q) на левом торце, имеющая равнодействующей силу P. Из условия равновесия

выделенной части имеем, что N = P, а поскольку x = const, получаем:
x =	N	.	(4.1)
	F

При центральном растяжении нагрузками q = const цилиндрический стержень с первоначальной длиной L (рис.4.4.) получает абсолютное удлинение L=L1 - L. Отношение абсолютного удлинения (при сжатии - абсолютного укорочения) к первоначальной длине бруса называется относительной продольной деформацией или относительным удлинением (укорочением):

x	L / L	(4.2)

34

(4.5)

Рис. 4.4. Изменение размеров бруса при центральном растяжении

Растяжение стержня сопровождается уменьшением его поперечных размеров. Отношение абсолютного сужения d = d - d1 к первоначальному размеру поперечного сечения d называется

	относительной поперечной деформацией		d	. Отношение относительной поперечной
		x	d

деформации к продольной, взятое по абсолютной величине, т.е.:

	x	,	(4.3)
	x

является величиной постоянной для данного материала и носит название коэффициента Пуассона. Для стали = 0,24…0,30; для чугуна = 0,23…0,27 (подробные сведения

приведены в справочнике [6, т./1/]).

В результате обобщения наблюдений за деформациями упругих тел установлено, что действующее напряжение пропорционально относительной деформации. Это условие называется законом Гука:

x 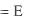x , (4.4)

где Е - коэффициент пропорциональности, называемый модулем упругости первого рода (модуль упругости при растяжении - сжатии) и характеризующий упругие свойства материала. Для стали Е = 200…210 ГПа; для чугуна Е = 115…160 ГПа (подробные сведения приведены в справочнике [6, т./1/]).

Если в выражение (4.4) подставить значения x и x cоответственно из уравнений (4.1) и

(4.2), то получим другую форму записи закона Гука:

L EFNL .

Произведение ЕF называют жесткостью бруса при растяжении (сжатии).

Уравнение прочности. При расчете на прочность детали, работающей на растяжение или сжатие, возникает вопрос: какое значение напряжения можно считать безопасным? Очевидно, это напряжение должно быть меньше некоторого опасного оп , при котором

возникает возможность разрушения детали или нарушения условий нормальной ее эксплуатации. Наибольшее безопасное значение напряжения называется допускаемым напряжением и обозначается . Тогда условие прочности при растяжении (сжатии) будет иметь вид:

		Nmax	,	(4.6)
	max	F

35

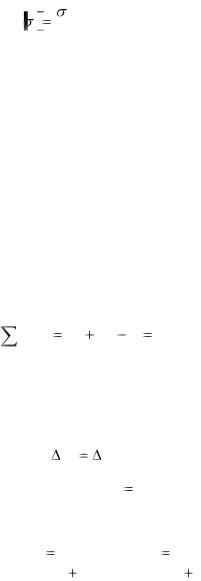
где N max - максимальное значение нормальной силы.

Допускаемое напряжение обычно выражается в долях от опасного:

	оп	,	(4.7)
	n

где n - коэффициент запаса (безопасности).

Последовательность решения задачи. Статистически неопределимой называется система, у которой неизвестных внутренних сил больше того количества уравнений, которое дает статика применительно к данной задаче. Определение действующих усилий в статически неопределимых конструкциях возможно лишь при учете деформаций, которые эти конструкции претерпевают.

На примере деформации стержня и втулки (из разных материалов), зажатых между двумя жесткими плитами (рис.4.5,а), рассмотрим порядок решения статически неопределимых задач.

1.Условно отбрасываем закрепления, вызывающие появление "лишних" реакций опор. Действие отброшенных закреплений заменяем приложенными неизвестными реакциями. Полученная система называется основной. В рассматриваемом примере реакцию стержня обозначим Rc , а втулки - Rв.

2. Для получившейся основной системы составляем уравнение статики:

P(x) Rв Rc P 0 .

(4.8)

3. В качестве дополнительных уравнений привлекаем так называемые уравнения совместимости деформаций (уравнения перемещений), отражающие физические условия деформации системы. Общее число уравнений статики и уравнений совместимости должно быть равно числу искомых неизвестных реакций.

Ввиду того, что под действием внешних сил втулка и стержень получают одинаковые

укорочения, уравнение совместимости Lв	Lс	при использовании формулы Гука:
	Rв Lв		Rc Lc	.
	Eв Fв		Ec Fc

Решив это уравнение совместно с уравнением (4.8), получим:

Rв			P		; Rc			P		.
	1		Ec Fc			1		Eв Fв
			Eв Fв					Ec Fc

По найденным усилиям Rв и Rc далее определяем напряжения и деформации, как показано

выше.

36

а)	б)
	Рис. 4.5. Статически неопределимые системы

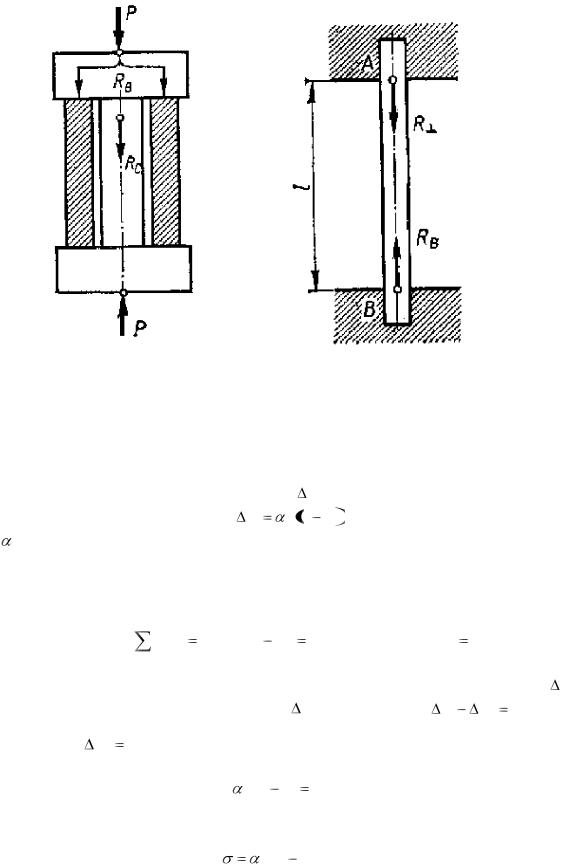
Температурные напряжения. Изменение температуры элементов статически неопределимой системы приводит к появлению в них температурных напряжений. Если стержень первоначальной длины L имеет возможность свободно расширяться и его температура

изменяется от t1 до t2, то температурное удлинение Lt			может быть подсчитано по формуле:
	Lt	L t2	t1 ,	(4.9)
где - коэффициент линейного температурного расширения стержня.
Рассмотрим напряжения,	возникающие	в стержне длиной L,		защемленном по концам
(рис.4.5,б) при температуре t1,в	случае последующего		повышения	температуры до t2. При

повышении температуры	возникают реакции	RA	и	RB , которые препятствуют удлинению
стержня.
Уравнение равновесия	P(x) 0 т.е. RA	RB	0	; следовательно, RA RB .
Уравнение совместности деформации составляем				из таких соображений. Если бы опоры А

не было, то под влиянием повышения температуры стержень удлинился бы на величину										Lt . Но
реакция опоры RA сжимает стержень на величину						LA . Очевидно, что Lt			LA 0 .
По закону Гука L		RAL	, следовательно, с учетом формулы (4.9) :
	A	EF
			L(t		t )		RAL	,
				2
					1		EF
откуда температурное напряжение:
			E(t2			t1 ) .				(4.10)
				37

4.3. Механические характеристики и испытания материалов

Основные характеристики. При расчетах на прочность деталей механизмов необходимо

знать механические свойства (характеристики) материалов: прочность,	упругость
(характеризуемую модулем упругости первого рода Е и коэффициентом Пуассона	), твердость

(способность данного тела препятствовать проникновению в него другого тела путем упругого или пластического деформирования либо путем разрушения части поверхности тела), пластичность (характеризуемую способностью материала давать остаточную деформацию).

Механические свойства определяются на специальных машинах и приборах при испытаниях образцов, изготовленных из данного материала. Различают испытания на растяжение, сжатие, изгиб, сдвиг, кручение и т.д. Большинство механических характеристик прямо или косвенно можно определить при испытании на растяжение, которое для металлов проводится в соответствии с ГОСТ 1497-73.

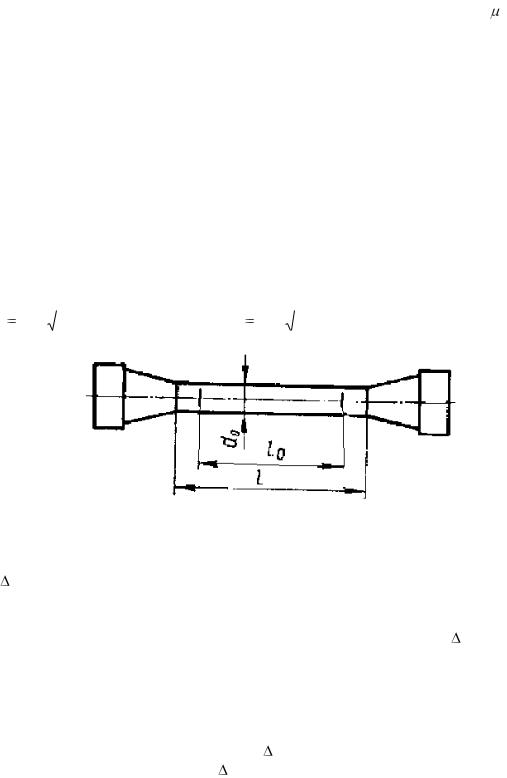
Испытание на растяжение. На растяжение испытывают образцы (рис.4.6), имеющие рабочую часть длиной L, и головки, предназначенные для закрепления в захватах испытательной машины. Удлинение определяется на начальной расчетной длине образца L0. Чаще всего применяются цилиндрические образцы. Отношение расчетной длины к начальному диаметру L0/d0 у "длинных" образцов принято равным 10; у коротких – L0/d0= 5. Применяются также образцы прямоугольного сечения. Расчетная длина их L0 связана с начальной площадью

поперечного сечения F0 такими же			зависимостями, как и у цилиндрических
образцов: L0 11.3 F0 - длинные образцы и L0			5.65 F0 - короткие образцы.

Рис. 4.6. Образец, применяемый при испытаниях на растяжение

Диаграмма растяжения. При испытаниях на растяжение получают зависимость удлинения L от нагрузки P в виде диаграммы растяжения. На рис. 4.7,а приведена диаграмма для малоуглеродистой стали. Диаграмма имеет ряд характерных точек. На участке ОА диаграмма прямолинейна - растяжение происходит с соблюдением закона Гука. При дальнейшем увеличении нагрузки прямая пропорциональность между P и L нарушается, но образец сохраняет упругие свойства вплоть до точки К. За этой точкой возникают заметные остаточные деформации. Начиная с точки С до точки D удлинение образца происходит без заметного увеличения внешней нагрузки. Материал, как говорят, "течет". Во время течения происходит перестройка кристаллических решеток материала образца и материал становится более прочным. Участок СD называется площадкой текучести.

В дальнейшем для увеличения удлинения L необходимо увеличить внешнюю силу P. Однако при этом соотношение между P и L закону Гука не подчиняется. При достижении на диаграмме точки В на образце образуется так называемая "шейка" - местное уменьшение сечения. Шейка быстро развивается. При этом значение внешней нагрузки уменьшается, хотя напряжение растет, и в точке Е наступает разрыв образца.

38

Диаграмму растяжения обычно перестраивают в более удобной системе координат	x	и

x (рис. 4.7,б). Форма диаграммы при этом не изменяется.

а )		б)
Рис. 4.7. Диаграммы растяжения образца из малоуглеродистой стали
Наибольшее напряжение, до которого материал следует закону Гука, называется пределом
пропорциональности	пц . Пределом упругости	y называется наибольшее напряжение,	до
которого материал не получает заметных остаточных деформаций. Предел текучести			T -
напряжение, при котором происходит рост деформаций без заметного увеличения нагрузки PT .
Предел прочности	B - отношение максимальной	силы PB , которую способен выдержать

образец, к его начальной площади поперечного сечения.

Для характеристики пластичности испытуемого материала используются две величины:

относительное удлинение при разрушении						Lk L0	100% и относительное сужение образца
						L0
	F0	Fmin	100%	. Длина образца LK	и минимальная площадь поперечного сечения шейки
		F0

Fmin после разрушения фиксируются при испытании.

Кроме указанных выше механических характеристик, диаграмма растяжения дает возможность определить энергетическую характеристику материала. Величина площади диаграммы растяжения в координатах P L (рис.4.7,а) характеризует работу, израсходованную на разрыв образца. Элементарная работа, произведенная действующей на образец силой P на приращении удлинения d L , равна dA Pd L , а вся работа, затраченная на разрыв образца

A Pd L , может быть посчитана как площадь диаграммы, ограниченная кривой OACDBE,

0

отрезком EG и осью абсцисс (рис. 4.7,а).

В пределах упругости полная работа, произведенная внешними силами при статическом нагружении, превращается в потенциальную энергию деформированного тела и выражается площадью треугольника ОАF: при удалении образца L и соответствующей ему силе P потенциальная энергия U P L / 2 . Потенциальная энергия, отнесенная к единице объема образца, называется удельной:

39

	P L	2
u	2F0 L 2 2E .		(4.11)

Выбор допускаемого напряжения. Определение величины допускаемого напряжения является одной из важных задач расчетов на прочность. Как следует из выражения (4.7), допускаемое напряжение получают как часть величины напряжения оп , соответствующего

опасному состоянию и определяемому при механических испытаниях материала. Для того

чтобы	избежать остаточных		деформаций, за величину	оп	для пластичных		материалов
принимают предел текучести			Т . В этом случае коэффициент запаса обозначают через
nT -	его называют	коэффициентом запаса по пределу текучести. Тогда					T / nT . Для
хрупких материалов (чугун, высокоуглеродистые закаленные стали и др.) за						оп	принимают
предел прочности		В , а под nB понимают коэффициент запаса по пределу прочности, поэтому

B / nB .

Выбор значения коэффициента запаса зависит от методов расчета, степени точности методов, свойств материалов, назначения конструкции и многих других факторов. Указания о конкретных значениях этих коэффициентов приводятся далее для различных случаев конструкций определенного назначения.

Твердость. Для определения твердости материала используют методы Бринелля (ГОСТ 9012-59), Роквелла (ГОСТ 9013-59) и Виккерса (ГОСТ 2999-75).

Числом твердости НВ по Бринеллю называется отношение нагрузки P, с которой вдавливается закаленный шарик в шлифованную поверхность образца, к площади F получаемого при этом отпечатка:

HB FP .

В соответствии со стандартом применяются шарики диаметром 2,5;5 и 10 мм. Минимальная толщина испытуемого образца должна быть не менее десятикратной глубины отпечатка.

По методу Роквелла о твердости судят по разности глубин, на которые проникает алмазный конус или стальной шарик диаметром 1,5875 мм при действии двух последовательно приложенных нагрузок (предварительной и общей). Для определения числа твердости применяют две шкалы. По шкале В (при вдавливании стального шарика) число твердости обозначается НRB. Для более твердых материалов по шкале С число твердости обозначается НRС (при вдавливании алмазного конуса).

	Число твердости по Виккерсу HV	P	является отношением нагрузки P, вдавливающей
		F

алмазную пирамиду в поверхность образца, к площади F боковой поверхности полученного пирамидального отпечатка.

40