2939

y		y			1		k 0	2k 0	2k	0	k 0
	21		20							32
					6		12	22			42
		1		1	(0		2	( 0.137078)			2 ( 0.137078)
			6
		0.255366)						0.866054;

x1 x0 h 0.523599.

Продолжая процесс вычислений, получаем:

i		2 :			x2		1.047197;					y12			1.242805;				y22			0.5003754;
i		3 :			x3		1.570796;					y13			0.999585;				y23			0.000889.
			Результаты численного решения задачи с шагами																						и
																						6			12
сведены				в таблицу 13.
																						Таблица 13
							Численное решение задачи Коши																Точное
	i																						решение
			xi																				y1		sin xi
							с шагом									с шагом
																		12
								6
							y1i		y2i							y1i		y2i
0			0				0		1						0			1					0
1			6		0.49967				0.86605						0.49998			0.86603					0.5
2			3		0.86548				0.50037						0.86599			0.50003					0.86625
3			2		0.99958				0.00088						0.99998			0.00006					1
			Используя правило Рунге, находим погрешность
	max		max			yk i (h)		yk i (h 2)								yk i (h) yk i (h 2)						0.00829
	1 i	3	1 k 2
							15								15							15

0.000055.

111

8. ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ

8.1. РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА МЕТОДОМ СЕТОК

Пусть в плоскости XOY дана область D , ограниченная кон-

туром C . Требуется найти непрерывную функцию u(x, y) , удов-
летворяющую внутри области D уравнению Лапласа
	2u(x, y)			2u(x, y)	0	(8.1)
	x 2			y 2
и граничному условию
	u(x, y)	C		f (x, y) ,		(8.2)

где f (x, y) - непрерывная функция, заданная в точках контура C . Решение этой задачи по методу сеток заключается в следую-

щем. Выбрав шаг h , проводятся прямые x ih , y kh , парал-

лельные осям координат, i и k принимают последовательные целочисленные значения. Точки пересечения этих прямых будем на-

зывать узлами сетки. Из отрезков эти прямых строится контур Ch максимально приближенный к контуру C . В результате получим область Dh , состоящую из узловых точек (рис.19).

Рис. 19

112

Приближенные значения искомой функции в точках ( xi , yk ) обозначим через ui,k , т.е. u(xi , yk ) ui,k .

Аппроксимируем частные производные

2u(x, y)

и

2u(x, y)

в

x2

y 2

каждом

внутреннем узле сетки центральными разностями второго

порядка

2u(xi , yk )

ui 1,k

2ui,k

ui 1,k

,

x2

h2

2u(x , y

k

)

ui,k 1

2ui,k

ui,k 1

i

y 2

h2

и заменим уравнение Лапласа конечно-разностным уравнением

ui 1,k 2ui,k

ui 1,k

ui,k 1

2ui,k

ui,k 1

0 .

h2

h2

После преобразования эта система имеет вид

ui,k

1

ui 1,k

ui

ui,k

ui,k 1

(8.3)

4

1,k

1

Для каждого узла сетки, лежащего внутри области Dh

(и не

лежащего на границе Ch ) составляем уравнение (8.3).

Значение функции

u(xi , yk )

в точках

(xi , yk )

Ch

принимаются

равным

значениям функции

f (x, y) в точках ( x, y )

ближайших к

точкам

( xi , yk ). В результате получим систему линейных алгеб-

раических уравнений относительно приближенных значений функции u(x, y) в узлах сетки ( xi , yk ).

При получении сеточных уравнений (8.3) была использована схема узлов, изображенная на рис.20. Набор узлов, используемых для аппроксимации уравнения в точке, называется шаблоном.

Таким образом, численное решение задачи Дирихле для уравнения Лапласа состоит в нахождении приближенных значений

ui,k искомой функции u(x, y) во внутренних узлах сетки. Для

113

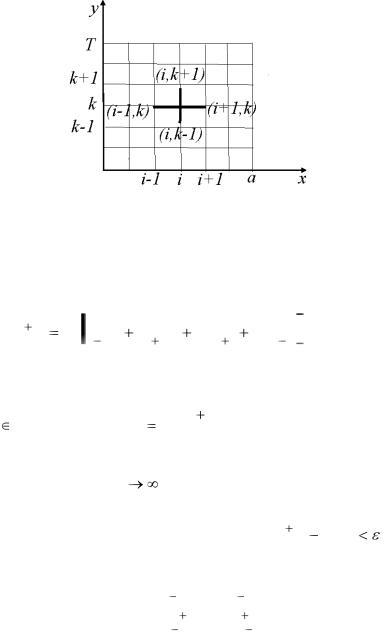
Рис. 20

определения величин ui,k требуется решить систему линейных

алгебраических уравнений (8.3). Такие системы обычно решаются одним из приближенных методов, например, методом итераций или методом Зейделя. Метод итераций состоит в построении последовательности вычислений вида

	(s 1)	1	(s)	(s)	(s)	(s)
	ui,k		ui 1,k	ui 1,k	ui,k 1	ui,k 1	(8.4)
		4

(верхним индексом обозначен номер итерации). Начальное при-

ближение ui(0),k выбирается	произвольно, можно во всех точках
(0)		umin	umax
( xi , yk Dh ) положить ui,k				, где umin	и	umax -
			2
наименьшее и наибольшее значения функции f (x, y)					в узловых
точках контура Ch . При s		последовательность ui(,sk)				сходится

к точному решению системы (8.3). В качестве условия окончания

	(s 1)	(s)
итерационного процесса можно принять max	ui, k	ui, k	,

где наперед заданная точность. Метод Зейделя отличается от ме-

(s)				(s)
тода итераций тем, что вместо ui 1,k		,		ui,k	1	в формуле (8.4) ис-
(s	1)			(s	1)
пользуются уже вычисленные ui	1, k		,	ui, k	1	, то есть

114

	(s 1)	1	(s 1)	(s)	(s)	(s 1)
	ui,k		ui 1,k	ui 1,k	ui,k 1	ui,k 1	(8.5)
		4

Погрешность приближенного решения, полученного методом сеток складывается из двух погрешностей: погрешности аппроксимации дифференциального уравнения разностными и погрешности, возникающей в результате приближенного решения системы разностных уравнений (8.3). Рассмотренная разностная схема обладает свойством устойчивости и сходимости. Устойчивость схемы означает, что малые изменения в начальных данных приводят к малым изменениям решения разностной задачи. Только такие схемы применяют в реальных вычислениях. Сходимость схемы означает, что при стремлении шага к нулю (т.е. при h 0) решение разностной задачи стремится к решению исходной задачи. Таким образом, выбрав достаточно малый шаг h , можно как угодно точно решить исходную задачу.

8.2. РЕШЕНИЕ СМЕШАННОЙ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ

ГИПЕРБОЛИЧЕСКОГО ТИПА МЕТОДОМ СЕТОК

Пусть

в

плоскости

XOY

дана

прямоугольная

область

D

(x, t)

0

x

a, 0

t

T .

Требуется найти

непрерывную

функцию u(x,t) ,

удовлетворяющую внутри области D дифферен-

циальному уравнению

2u

c2

2u

f (x,t) ,

0

x a,

0

t

T,

(8.6)

t 2

x2

начальному условию

u(x,0)

(x) ,

(8.7)

граничным условиям

u(0,t)

1(t),

u(a,t)

2 (t),

0

t

T .

(8.8)

Для построения разностной схемы

решения задачи

(8.6) –

(8.8) выберем шаги h,

l

по x

и

t , и построим

в

области

D

(x, t)

0

x

a,

0

t

T

сетку

xi

ih ,

i

0,1,2,..., n,

n

a

,

tk

k ,

k

0,1,2,..., m ,

m

T

.

Зна-

h

чение функции u(x,t)

в

узлах сетки называются сеточной функци-

115

ей ui,k u(xi,tk ) , приближенные значения которой требуется най-

ти.

Для получения разностного уравнения аппроксимируем частные производные второго порядка в каждом внутреннем узле сетки на шаблоне, показанным на рис. 20. Эти производные, выраженные через разностные отношения, будут иметь вид

2u(xi , tk )

ui, k 1

2ui, k

ui, k 1

,

t 2

2

2u(xi , tk )

ui 1,k

2ui,k

ui 1,k

.

x 2

h2

Здесь ui,k

– приближенное

значение функции u(x,t)

в узле

( xi ,tk ). После такой замены

получаем следующую разностную ап-

проксимацию уравнения (8.6)

ui,k

1

2ui,k

ui,k

1

c2

ui

1,k

2ui,k

ui

1,k

f (x ,t

) .

(8.9)

k

2

h2

i

После преобразования уравнения (8.9) получаем трехслойную

разностную схему

ui,k

2(1

c2

2

)ui,k

ui,k

c2

2

(ui 1,k

ui

1,k )

2 f (xi,tk ). (8.10)

1

h

2

1

h2

Схема (9.10) называется трехслойной потому, что связывает

между собой

значения ui,k

функции

u(x,t)

на трех временных

слоях: с номерами k

1, k, k

1. Схема (8.10) явная, т.е. позволяет в

явном виде выразить

ui,k

через значения

u

с предыдущих двух

слоев.

Численное решение задачи состоит в вычислении приближен-

ных

значений

ui,k

решения u(x,t)

в узлах

(xi , tk )

при

i 1,..., n 1,

k

1,..., m

1 .

Алгоритм

решения основан на

том, что решение на каждом следующем слое ( k

2,3,..., m )

мож-

но

получить

пересчетом

решений с

двух

предыдущих

слоев

116

( k	2,3,..., m 1 ) по формуле (8.10). На нулевом временном слое
( k	0 ) решение известно из начального условия ui,0	(x) . Для

вычисления решения на первом слое ( k 1 ) можно использовать такой прием, состоящий в том, что если положить

		u	(x,0)	u(x,	)	u(x,0)	,	(*)
		t
то ui,1 ui,0	(x),		i 1,2,..., n		1.	Теперь для вычисления ре-

шений на следующих слоях можно применять формулу (8.10). Решение на каждом следующем слое получается пересчетом решений с двух предыдущих слоев по этим формулам.

Описанная выше схема аппроксимирует задачу (8.6) – (8.8) с точностью 0(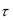 h2 ) . Невысокий порядок аппроксимации по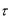

объясняется использованием слишком грубой аппроксимации для производной по t в формуле (*).

Схема устойчива, если выполнено условие Куранта 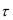h . Это означает, что малые погрешности, возникающие, например, при вычислении решения на первом слое, не будут неограниченно возрастать при переходе к каждому новому временному слою. При выполнении условий Куранта схема обладает равномерной сходимостью, т.е. при , h 0 решение разностной задачи равномерно стремится

к решению исходной смешанной задачи (8.6) – (8.8).

Недостаток схемы в том, что как только выбрана величина шага сетки h в направлении x , появляется ограничение на величину шага 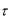по переменной t . Если необходимо произвести вычисления для большого значения величины T , то может потребоваться большое количество шагов по переменной. Указанный недостаток характерен для всех явных разностных схем.

9.3.РЕШЕНИЕ СМЕШАННОЙ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА МЕТОДОМ СЕТОК

Пусть		в	плоскости	XOY	дана прямоугольная область
D (x, t)	0	x	a, 0 t	T .	Требуется найти непрерывную

функцию u(x,t) , удовлетворяющую внутри области D дифференциальному уравнению

117

	u	c2		2u	f (x,t) , 0 x		a, 0	t	T,	(8.11)
	t		x2
начальному условию					u(x,0)	(x) ,				(8.12)
граничным условиям
u(0,t)		1(t),			u(a,t)	2 (t),	0	t	T .	(8.13)

К задаче (8.11) - (8.13) приводит, в частности, задача о распространении тепла в стержне длины a , на концах которого поддерживается заданный температурный режим.

Для построения разностной схемы решения задачи (8.11) - (8.13) по-

строим в области

D

(x, t)

0

x

a,

0

t

T

равномер-

ную прямоугольную сетку с шагом h в направлении x

и шагом

-

в

направлении

t (рис.

21) .

Обозначим

узлы

сетки

через

(x1, t1 ),..., (xi , tk ) ,…, а приближенные значения функции u(x,t)

в

этих узлах - ui,k .

Тогда

xi

ih ,

i

0,1,2,..., n ,

h

a n , n

a

;

h

tk

k , k 0,1,2,..., m ,

T m ,

m

T

.

Для получения разностного уравнения заменим частные производные второго порядка в каждом внутреннем узле сетки разностными отношениями

	u(x ,t		k 1		) ui,k 1 ui,k
	i							,
		t
2u(xi , tk 1 )				ui 1,k 1 2ui,k 1				ui 1,k 1	.
x 2							h2

После такой замены получаем двухслойную разностную схе-

му

ui,k 1	ui,k		c	2	ui 1,k 1	2ui,k 1	ui 1,k 1	f (xi , tk 1 ) ,
						h2
i 1,2,..., n 1,					k	1,2,...., m 1,
ui,0	(xi ) ,				i	0,1,2,..., n ,
u0,k	1(tk ) ,				k	0,1,2,..., m .

118

un,k

2 (tk ) ,

k 0,1,2,..., m .

Для аппроксимации частных производных второго порядка рассматриваемой задачи шаблон изображен на рис.17, из которого видно, что полученная схема является неявной.

Рис. 17

Запишем разностное уравнение следующим образом

	c2	ui 1,k 1 (1	2c2	)ui,k 1	c2	ui 1,k 1 ui,k f (xi , tk 1) . (8.14)
	h2		h2		h2

Схема (8.14) аппроксимирует уравнение (8.11) только во внутренних узлах сетки, поэтому число уравнений в схеме (8.14) меньше

числа неизвестных ui,k . Недостающие уравнения получаем из граничных условий

	u0,k	1(tk ) ,	un,k	2 (tk ) .		(8.15)
Схема (8.14)-(8.15) неявная, поэтому значения					ui,k	находят
как решение	системы	линейных уравнений (8.14).			Для решения
этой системы	можно применять любой алгоритм решения систем
линейных уравнений, однако она			обладает трехдиагональной мат-
рицей и рациональнее всего решать ее методом прогонки.						Таким
образом, последовательно проходя все слои t				k , начиная с нуле-

119

вого слоя, для которого известны значения ui,0 (xi ) , находим сеточную функцию ui,k , значения которой в узлах сетки прибли-

женно заменяют значения искомого решения исходного уравнения. Замечательным свойством неявной схемы (8.14) является ее

устойчивость при любых значениях 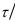h2 0 . Явная схема оказывается устойчивой только при 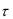h2 2 . Это означает, что вычисле-

ния по явной схеме придется вести с очень малым шагом по 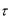, что может привести к большому числу вычислений. В неявной схеме вычисления на одном шаге требуют больше операций, но зато величину шага можно выбрать как угодно большой без риска нарушить устойчивость системы. Все это позволяет сократить число вычислений. Для получения точного решения следует проводить дробление шага.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. – М: Высшая школа, 1994. 544с.

2.Бахвалов Н.С., Жидков Н.О., Кобельков Г.Н. Численные методы. – М: Высшая школа, 1987. 518с.

3.Воробьев Г.Н., Данилова А.Н. Практикум по вычислительной математике. – М: Высшая школа, 1990. 208с.

4.Демидович Б.Н., Марон И.А. Основы вычислительной математики. – М: Наука, 1970. 502с.

5.Гутер Р.С., Овчинский Б.В. Элементы численного анализа

иматематической обработки результатов опыта.: Наука, 1970. 432с.

6.Ракитин В.И., Первушин В.Е. Практическое руководство

по методам вычислений с приложением программ для персональных компьютеров. – М: Высшая школа, 1998. 376с.

7.Плис А.И., Сливина Н.А. Лабораторный практикум по высшей математике. – М: Высшая школа, 1994. 206с.

8.Семенов М.П., Катрахова А.А, Жучкова В.В. Основы численных методов. – Изд-во ВГТУ, 1997. 62с.

8.Турчак Л.И. Основы численных методов. – М: Наука, 1982. 318с.

120