
3323
.pdf
|
|
|
b |
|
|
|
n |
|
|
|
|
f |
x dx lim |
|
f k |
xk . |
|
|
|
|
a |
|
n |
k |
1 |
|
|
|
|
|
|
|
|||
Числа a |
и b |
называются нижним и верхним пределами |
||||||
интегрирования, |
f |
x |
-подынтегральной функцией, x - |
|||||
переменной |
интегрирования, |
|
отрезок |
a, b -областью |
||||
(отрезком) интегрирования. |
|
|
|
|
||||
Функция y |
f |
x , |
для которой существует определѐнный |
|||||
интеграл на отрезке |
a, b , называется интегрируемой на этом |
|||||||
отрезке.
На вопрос о существовании определенного интеграла
дает ответ теорема Коши. |
|
|
Теорема Коши: Если функция y |
f |
x непрерывная на |
отрезке a, b , то она интегрируема |
на |
этом отрезке (без |
доказательства).
Таким образом, непрерывность функции является достаточным условием интегрируемости функции. Среди разрывных функций могут быть как интегрируемые, так и не интегрируемые функции.
В частности, можно доказать, что для всякой ограниченной на отрезке a, b функции, имеющей на нѐм
конечное число точек разрыва, существует определѐнный интеграл.
|
|
8.2. Геометрический смысл определенного интеграла |
||||||
|
|
Пусть на отрезке |
a, b |
задана |
непрерывная функция |
|||
y |
f |
x |
0 . Фигура, ограниченная сверху графиком y |
f |
x , |
|||
снизу осью Ox , с боков двумя вертикальными прямыми x |
a |
|||||||
и |
x |
b , |
называется |
криволинейной |
трапецией. |
Найдѐм |
||
площадь этой фигуры. |
|
|
|
|
|
|||
|
|
Для |
этого разобьѐм |
отрезок |
a, b на n |
частей |
||
произвольным образом. Обозначим длину частичных отрезков
141

x1 x1 x0 , x2 x2 x1 , ... xn xn xn 1 . В каждом из частичных отрезков выберем произвольную внутреннюю точку
k |
|
|
xk |
k xk 1 |
(k=1,…, n ). Вычислим значение функции f(x) в |
этих |
точках: |
f ( k ) (k=1,… n ). Через точки деления |
x1 , x2 ,..., xn 1 проведем прямые, параллельные оси Oy . Каждую
часть криволинейной трапеции, расположенную между вертикальными прямыми, заменим прямоугольником с тем же
самым основанием xk и высотой f( |
k ) (k=1,… n ). Площадь |
каждого прямоугольника равна f ( k ) |
xk . |
При этом криволинейная трапеция заменяется ступенчатой фигурой (рис. 28), площадь которой равна сумме площадей элементарных прямоугольников:
Sn  f
f  0
0  x0
x0 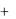 f
f  1
1  x1 ...
x1 ...  f
f  k
k  xk ...
xk ...  f
f  n 1
n 1  xn 1 =
xn 1 =
n
f k xk .
k 1
y
y  f x
f x
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
3 |
|
n |
|
|
|
|
|
|
|
|||
|
1 |
|
2 |
|
|
|||
O a x0 x1 |
x2 |
x3 |
xn 1 b xn |
|
||||
Рис. 28.
142

Площадь Sn ступенчатой фигуры является лишь
приближѐнным значением искомой площади криволинейной трапеции. Очевидно, что это приближение будет тем более точным, чем меньше длина частичных отрезков и больше их число. Способ разбиения отрезка на n частей при n  , если длина наибольшего частичного отрезка стремится к нулю, т.е.
, если длина наибольшего частичного отрезка стремится к нулю, т.е.
0 , называется способом равномерного измельчения.
При равномерном измельчении отрезка a, b . ломаная линия будет теснее примыкать к кривой y f (x) , а точность
приближения площади криволинейной трапеции площадью ступенчатой фигуры будет возрастать.
За точное значение площади криволинейной трапеции
принимают предел, к |
|
которому стремиться Sn при |
|||
равномерном измельчении отрезка |
a, b |
(если такой предел |
|||
существует): |
|
|
|
|
|
|
|
|
n |
|
b |
S lim Sn |
lim |
f ( |
k ) xk |
f x dx . |
|
n |
n |
k |
1 |
|
a |
|
|
|
|||
Таким образом, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции, в чем и состоит геометрический смысл определенного интеграла.
8.3. Работа переменной силы
|
Пусть |
материальная точка M |
перемещается |
под |
|
действием силы F |
по оси Ox . Сила F |
действует вдоль оси |
|||
Ox |
и является функцией координаты |
x . Найдем работу A |
|||
силы F x |
по перемещению точки M вдоль оси Ox от точки |
||||
x |
a до точки x |
b . Для этого разобьѐм отрезок a, b |
на n |
||
частей произвольным образом. Обозначим длину частичных отрезков x1 x1 x0 , x2 x2 
 xn
xn  В
В
143

каждом из частичных отрезков выберем произвольную
внутреннюю точку |
k |
xk |
k |
xk 1 (k=1,…, n ). |
|
Вычислим значение силы в каждой точке |
k : |
||||
F1 |
f |
1 , F2 |
f ( |
2 ), ... Fn f ( |
n ) . |
Если разбиение достаточно мелкое, то сила Fk незначительно меняется на элементарном отрезке xk 1 , xk и может приближенно считаться на этом отрезке постоянной. В
этом |
случае |
элементарная |
|
работа |
на |
частичном отрезке |
|||||||
xk 1 , xk |
равна |
Ak |
f ( |
k ) xk . |
Тогда |
работа силы |
при |
||||||
перемещении вдоль всего отрезка |
a, b |
примерно равна сумме |
|||||||||||
элементарных работ: |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
An |
|
|
f ( |
k ) xk . |
|
|
||
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
Точное значение работы А определяется как предел |
An , |
|||||||||||
при |
n |
, |
если |
измельчение |
отрезка |
a, b |
производится |
||||||
равномерным образом: |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
A |
lim |
f ( |
k ) |
xk , |
|
|
||
|
|
|
|
|
|
n |
k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
что и соответствует определенному интегралу |
F x dx . |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
Таким |
образом, |
физический |
смысл |
определенного |
||||||||
интеграла –это работа переменной силы F x , действующей на материальную точку M на отрезке a, b .
8.4.Свойства определенного интеграла
1.Постоянный множитель можно выносить за знак определѐнного интеграла:
144

b |
b |
|
Af (x)dx A f (x)dx . |
a |
a |
2. Если функции f(x) и g(x) интегрируемы на a, b , то
интегрируема на этом отрезке и сумма данных функций, т.е. определѐнный интеграл от алгебраической суммы равен алгебраической сумме интегралов от слагаемых:
b |
b |
b |
f ( x) g( x) dx |
f (x)dx |
g(x)dx . |
a |
a |
a |
Свойство 2 распространяется на любое конечное число слагаемых. Следует отметить, что свойства 1 и 2 выделяются, образуя свойство линейности операции интегрирования:
b |
b |
b |
|
Af (x) Bg(x) dx A f (x)dx B g(x)dx . |
|
a |
a |
a |
b |
a |
|
3.f (x)dx 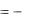 f (x)dx .
f (x)dx .
a b
Доказательство свойства становится очевидным, если учесть то, что при назначении нового порядка разбиения
отрезка a, b от b |
к a в интегральной сумме меняется знак |
|||
каждого |
xk на противоположный. |
|
||
4. |
Свойство |
аддитивности: Если функция y f x |
||
интегрируема на отрезке a, b |
и a<c<b, то |
|||
|
b |
|
c |
b |
|
|
f (x)dx |
f (x)dx |
f (x)dx , |
|
a |
|
a |
c |
т.е. интеграл по всему отрезку равен сумме интегралов по частям этого отрезка.
Свойство 4 справедливо при расположении точки c вне отрезка a, b , если функция f x продолжает оставаться интегрируемой на каждом из получающихся отрезков.
продолжает оставаться интегрируемой на каждом из получающихся отрезков.
145

5. Если функция f (x) 0 интегрируема на отрезке a, b
b
(a<b), то f (x)dx 0 .
a
6. Если f(x) и g(x) интегрируемы на отрезке a, b (a<b) и
удовлетворяют на нѐм равенству |
f (x) g(x) , то |
b |
b |
f (x)dx |
g(x)dx . |
a |
a |
7. Если f(x) интегрируема |
на отрезке a, b и a<b, то |
модуль определенного интеграла не превосходит интеграла от модуля подынтегральной функции, т.е.
b |
b |
|||
f (x)dx |
|
f (x) |
|
dx . |
|
|
|||
a |
a |
|||
8. Если функция f(x) интегрируема на a, b (a<b) и числа m и М являются наименьшим и наибольшим значениями
функции f |
x |
на отрезке |
a, b , т.е. выполняется неравенство |
m f (x) |
M , то |
|
|
|
|
|
b |
|
|
m(b a) |
f ( x)dx M (b a) . |
|
|
|
a |
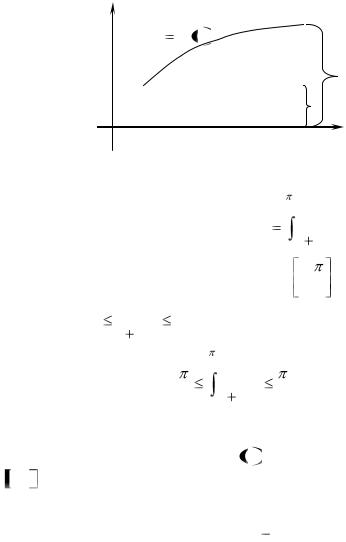
Если |
f |
x 0 , то свойство 8 допускает наглядную |
|
геометрическую интерпретацию: площадь криволинейной трапеции, соответствующей определенному интегралу
b
f (x)dx , заключена между площадями прямоугольников с
a
отрезком a, b в основании и высотами, равными m и M , как
показано на рис. 29.
Данное свойство используется для оценки определенного интеграла.
146
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
y |
|
f |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
O |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
x |
|
|||||
|
|
|
|
|
|
|
|
|
Рис.29. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
dx |
|
|
||||
Пример 8.1. Оценить интеграл: I |
|
|
|
|
|
|
. |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 1 |
|
|
tgx |
|
||||||
Решение: |
Поскольку |
на |
отрезке |
0, |
|
|
|
выполняется |
|||||||||||||||||
4 |
|
|
|||||||||||||||||||||||
неравенство |
1 |
|
1 |
|
|
1, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
1 tgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
8 |
0 1 |
tgx |
4 |
|
|
|
|
|
||||||||||
9. Теорема о среднем для определѐнного интеграла. |
|||||||||||||||||||||||||
Теорема: |
Если функция |
f x непрерывна на отрезке |
|||||||||||||||||||||||
a, b , то внутри отрезка найдется хотя бы одна точка c такая, что
b
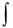 f (x)dx
f (x)dx 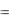 f (c)(b a) .
f (c)(b a) .
a
Геометрический смысл теоремы о среднем состоит в том, что криволинейная трапеция, соответствующая определенному
147
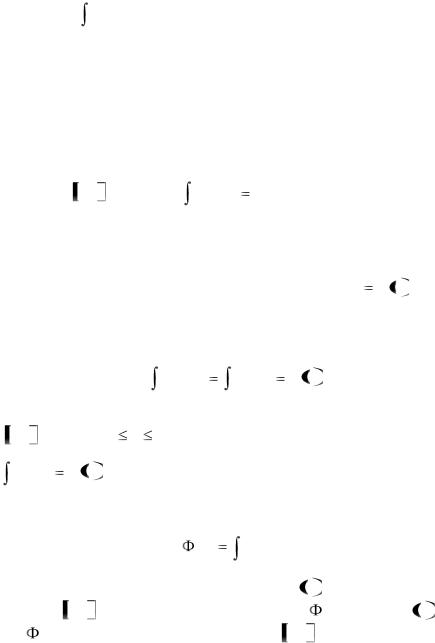
b
интегралу f (x)dx , равновелика прямоугольнику с длиной
a
основания (b-a) и высотой f(c).
8.5. Определѐнный интеграл с переменными верхним пределом.
Пусть неотрицательная функция f(x) интегрируема на
|
b |
отрезке a, b . Тогда |
f (x)dx S представляет число, |
|
a |
соответствующее площади криволинейной трапеции. Если верхний предел интегрирования b будет менять свое положение, то, очевидно, будет меняться и площадь изменяющейся криволинейной трапеции, т.е. S S b . В определѐнном интеграле переменную интегрирования можно обозначить любым другим символом, например t :
|
b |
|
b |
|
|
f (x)dx |
f (t)dt S b . |
|
|
|
a |
|
a |
|
Рассмотрим |
отрезок |
с |
переменным верхним |
пределом |
a, x , где a |
x b . |
Тогда определенный |
интеграл |
|
x
f (t)dt S x оказывается функцией переменного верхнего
a
предела интегрирования
|
|
x |
|
|
|
|
( x) |
f (t)dt . |
|
|
|
|
|
a |
|
|
|
Теорема |
Барроу: Если функция |
f x |
непрерывна |
на |
|
отрезке a, b , |
то производная от функции |
(x) равна f |
x , |
||
т.е. (x) есть первообразная для f(x) на |
a, b : |
|
|
||
148

(x) 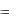 f (x) .
f (x) .
Другими словами: производная от определѐнного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой аргумент t заменяется на
x : f (t) t x  f (x) .
f (x) .
Из теоремы Барроу следует, что неопределенный интеграл может быть представлен с использованием определенного интеграла с переменным верхним пределом:
x
f (x)dx  (x) C
(x) C  f (t)dt C .
f (t)dt C .
a
8.6. Формула Ньютона-Лейбница
Пусть функция y  f x
f x интегрируема на отрезке a, b .
интегрируема на отрезке a, b .
Тогда способ вычисления определенных интегралов может быть получен с помощью формулы Ньютона-Лейбница.
Теорема: Если функция f x непрерывна на отрезке a, b и F x
и F x есть какая-либо ее первообразная, то имеет место формула Ньютона-Лейбница:
есть какая-либо ее первообразная, то имеет место формула Ньютона-Лейбница:
b
 f (x)dx F (b) F (a) .
f (x)dx F (b) F (a) .
a
Формула Ньютона-Лейбница представляет удобный способ вычисления определенного интеграла: сначала находится первообразная, затем вычисляется разность значений первообразной на концах отрезка a, b .
Пример 8.2. Вычислить определенный интеграл 5e ln x dx.
e x
Решение:
149

5e |
ln x dx |
5e |
ln x |
2 |
5e |
1 |
ln 5e 2 |
ln e 2 |
|
ln x d ln x |
|
|
|||||
|
x |
2 |
|
e 2 |
||||
e |
e |
|
|
|
||||
|
|
|
|
|
|
|
||
|
|
|
|
1 |
ln 5 1 2 |
1 |
|
1 |
ln2 5 2 ln 5 . |
|
|
|
||
2 |
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||
|
Пример 8.3. |
|
|
Вычислить |
определенный интеграл |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
esin x cos x dx. |
|
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
esin x cos x dx |
|
|
esin x d sin x |
esin x |
2 |
e 1 . |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
|
0 |
|
|
|
|
0 |
|
||||
8.7. Интегрирование по частям в определѐнном интеграле.
Пусть функции u(x) и v(x) непрерывно дифференцируемы на отрезке a, b . Дифференциал произведения функций равен
d(uv) udv vdu .
Интегрирование этого тождества на отрезке a, b дает
дает
b |
b |
||
udv (uv) |
|
ba |
vdu . |
|
|||
|
|
||
a |
a |
||
Раскрывая дифференциалы, фигурирующие в равенстве, получаем формулу интегрирования по частям в определенном интеграле:
b |
b |
||
v ( x)u( x)dx u( x)v( x) |
|
ba |
v( x)u ( x)dx . |
|
|||
|
|
||
a |
a |
||
Подобно тому, как в неопределенном интеграле выделяются три случая представления подынтегрального выражения в виде произведения u и dv , так же и при
150
