3841

		= −	ln			−		+	( )	(3.7)
Стохастические			ДУ	(3.4)-(3.7)				исследованы		наиболее

полно, дают адекватное описание СП во многих радиотехнических системах и позволяют получить замкнутые выражения для алгоритмов оценивания сигналов. Однако системы, базирующиеся непосредственно на таких уравнениях, как правило, не могут быть реализованы и исследованы из-за отсутствия необходимых стабильных нелинейных элементов аналоговой техники. В связи с этим на практике осуществляется переход от непрерывных к дискретным во времени системам на основе различных разностных схем [80,82]. Для обеспечения соответствия разностной схемы и уравнений вида (3.3), (3.4) от вычислительной техники требуется высокое быстродействие и большая точность представления чисел.

Стохастические разностные уравнения (3.3) свободны от этого недостатка, так как представляют последовательность чисел, для формирования которой можно воспользоваться методами цифровой техники. Поэтому в задачах с нелинейными моделями наблюдений, но при гауссовских компонентах, системы с дискретным временем имеют очевидные преимущества при технической реализации. Вместе с тем, при отличии ПРВ случайных последовательностей (3.3) от гауссовских возника-

(		,В− 1)	определения нелинейных функций	(		, )	и
ет		задача	по заданным распределениям.

ряде задач желательно построить (синтезировать) нелинейное уравнение (3.3) на основе априорных данных о виде безусловного одномерного распределения. К сожалению, такого же простого пути, какой существует для построения моделей (3.5)-(3.7), здесь нет. В работе [15] синтез марковской модели приводится не на основе априорных статистических характеристик СП, а на экспериментальных данных. При этом

решение получено лишь			для			ограниченного клас-
са линейных функций (		, ),	(			, −1).	Полученные
			131

модели марковских СП используются для решения задач прогноза.

Рассмотрим асимптотический подход для решения поставленной задачи, основанный на предположении о существовании предельного стохастического ДУ Ито [44, 91]

для заданного( ) =						( ,					)				+		( , )									( )			( )							(3.8)
			разностного														стохастического уравнения (3.3),
записанного в виде
	−		= (									,	;)+					(					,		− 1)											(3.9)
где
	= 0;								= 1
	Будем связывать значения																								и			c моментами време-
ни		=	+
	и				. При условии существования предельных
соотношений для детерминированных функций
	( ( ),					+					) −				( )								( ( ),					) +			(					),
																		=
							( +								)
перепишем (3.9) в форме,														позволяющей найти характеристики
															=						( ) +					(			)
приращений			−						:
		−					=					(			,					+					( )						( )					,
где										(							)
	(					) =						(			( ), +								)− ( )) ( )
			,																														,
																					(		+			)
	( ) = { ( )}, =														(		+				)	,				( ) = (										, −1),
																	( )

где, – независимые СВ, распределенные по нормальному закону с нулевым математическим ожиданием и единичной дисперсией.

132

3.4.Моделислучайныхпроцессовввидевременныхрядов.

3.4.1.Авторегрессионные модели случайных последовательностей

Пусть последовательность СВ удовлетворяет стохастическому уравнению

=

,

,

,

= 1,2,…

(3.10)

с начальным условием

где

– некоторые

функции;

=– заданная

последовательность неза-

и

висимых СВ,=называемая, , ,…

порождающейиливозмущающей после-

довательностью. Уравнение (3.10) представляет собой простейшую

авторегрессионнуюмодельСП = { , , ,…}[49].

Рис. 3.2. Процессы авторегрессии первого порядка

В качестве возмущающей последовательности чаще всего используется последовательность стандартных независимых гауссовских СВ. В случае линейности функции процесс также будет гауссовским, а при соответствующем вы-

133

боре нелинейных функций и негауссовских возмущений можно получить широкий класс негауссовских процессов [12, 74].

Примером марковской СП может быть процесс авторегрессии 1-го порядка, полученный с помощью линейного преобразования последовательности , ,… ,… независимых гауссовских СВ { } по следующему правилу:

=		+		, = 2,3,..				(3.11)
	Каждое | | < 1;					= 0;		=
				очередное значение				содержит часть преды-
дущего			и добавку в виде независимой СВ [10, 16].
	На рис. 3.2 представлены типичные графики реализаций

такого процесса при различных значениях параметра , входящего в модель (3.11). Во всех случаях параметр , влияющий только на масштаб по оси ординат, выбран равным единице. Из этих рисунков видно, что при , близких к единице, процесс становится более гладким; при малых , напротив, значения процесса слабо зависимы между собой; при отрицательных корреляция между соседними значениями процесса

отрицательна, поэтому он часто меняет знак.
	При выборе начального значения				,	обеспечивающего
стационарность и постоянство дисперсии								па-
раметр		равен	коэффициенту	корреляции между лю-
					{	} =	,

быми двумя соседними значениями СП. Действительно, ум-

ножая			левую	и правую	часть	(3.11)		на	} =	и	нахо-
				.	получим		{				или
дя математическое ожидание,
	=	{	}/
		Повторяя аналогичные операции после подстановки в
уравнение				(3.11)	=	+		,	=		+

…, можно записать следующую формулу для КФ:

где	( ) =	{	}	= | | =	| |,
			134

Таким образом=,	−ln	;		=	1 −		.

СП (3.1) имеет экспоненциальную КФ. В то же время СП (3.11) является марковской, поскольку лю-

бые вероятностные характеристики значения			полностью оп-
ределяются только предшествующим значением СП				. При
заданном	формула (3.17) позволяет найти все характери-
стики без	учета	предыстории,	т. е.	значений

,,…, СП. Так, условная ПРВ

=

√

−

(

−

)

(3.12)

может быть получена из ПРВ

правил

ПРВ

с учетом

связи

и

нахождения

= √

−

записать выражение и для совместного

функций СВ. Легко=

−

числа n членов рассмотренной

распределения

произвольного

марковской СП:

(

, ,…,

) =

(

)

=

= (

( −

(3.13)

)

1

−

1

)

√2

Поскольку вид всех ПРВ2

перехода (3.12) не зависит от

номера члена СП, то уравнение (3.11) представляет однородную марковскую СП. Для стационарности необходимо вы-

брать		СВ	таким		образом, чтобы		все	безусловные ПРВ
(3.11)( ),		= 1,2,…,		были одинаковыми. Проведенный анализ
		показывает,			что в стационарном			случае все		члены
{ } последовательности						имеют нулевое среднее и дисперсию
=	( Кроме).		того,		CП	гауссовская,		так как	получена
в результате линейного преобразования{ }							гауссовских		СВ	.
						135

Таким образом, ПРВ всех значений стационарной последовательности (3.11) будут иметь следующий вид:

При( ) =	√	2	−	2	,	= 1,2,…, .
		1
этом начальное значение формируется как нор-
мальная СВ	с		нулевым		средним	и дисперсией ,

а последующие члены последовательности образуются в соответствии с рекуррентным соотношением (3.11).

Уравнения вида (3.11), которые часто называются уравнениями авторегрессии или стохастическими разностными уравнениями, представляют весьма узкий класс гауссовских марковских СП с экспоненциальной КФ. Вместе с тем имеются различные возможности для существенного расширения этого класса [10, 49]. Одной из них является писание СП с помощью авторегрессионных (АР) уравнений более высоко-

го порядка:

+ +

+

, = 2,3,…,

(3.14)

где

=

+

с

m-порядок авторегрессии. С помощью подбора коэффици-

,

,…,

можно

получить гауссовские

СП

,

ентов

разнообразными корреляционными свойствами [10]. Дейст-

вительно,

умножая

(3.13)

на

и

нахо-

дя математические ожидания,

получим

после

деления

на

ний=КФ{:

}, = 1,2,…,

,

следующее соотношение для значе-

( ) =

( −1) +

( − 2)+ +

( − ),

Общее решение этого

> 0

(3.15)

разностного уравнения в стацио-

нарном случае представляется суммой экспонент [82]:

где

=

( ) =

|

|

+

| |

+ +

| |

,

; -

,

,

= 1,2,…,

корни характеристического

уравнения

−

−

− −

= 0.

. Требование

стационарности СП (3.14) выполняется, если

< 0

, т.е. ко-

гда

все

корни

,

= 1,2,…,

136

уравне-

характеристического

ния лежат внутри единичного круга на комплексной плоскости.

Подставляя в (3.15) значения

получим из-

вестную систему уравнений Юла-

Уокера [10,16]:

= 1,2,…,

+

(1)

+ +

( −1) = (1);

+ +

( −2) = (2);

(1)+

………………………………………………………

Решение( − 1)+

(

− 2)+ +

=

(

).

,

,…,

,

этой системы позволяет найти коэффициенты

уравнения авторегрессии (3.14) по заданным или

оцененным

на

основе

эксперимента

ям (1В),

(2),….качестве, ( ) КФ СП.

примера

рассмот-

рим процесс авторегрессии второго

порядка:

−

ходимо+,

,

= 2,3,…,

. Для стационарности

процесса необ-

=

+

чтобы

корни

характеристического уравнения

− = 0 лежали внутри единичного круга, т. е. чтобы па-

раметры и находились в треугольной области, показан-

ной на рис. 3.3[10,16].

Рис. 3.3. Область значений коэффициентов и

137

стационарного СП

Значения КФ стационарной СП связаны между собой

рекуррентным

соотношением

(

и .

,

с

начальными

условиями

(1) =

/(1−

|

|

( ) =

−1) +

)

|

| |

|

| |

(

Из этого соотношения следует,

что

−2),

> 0,

(0) = 1

где

= ln

( ) =

= ln

+

и

=

корни

+

,

,

,

−

характеристического

уравнения;

) ;

= 1 −

(

)

; . Дисперсия СП

находится

по формуле= ( )(:

двух уравнений

( ) . . Система

Юла-Уокера =

(

)

=

(2)

по-

зволяет

+

(1) =

(1),

(1)+

определить коэффициенты

и

уравнения авторег-

рессии

по

заданным

или

измеренным

значениям

(1)

Вид(2)

КФ.

и

КФ определяется областью треугольника допусти-

мых значений коэффициентов

и . (рис. 3.3).

ния

Если

+4

0

,

корни характеристического

уравне-

действительны и КФ представляет сумму двух затухаю-

щих экспонент.

При

,

> 0

(область I

на рис. 3.3)

корни

имеют

разные

знаки:

. Отрицательному

> 0

корню соответствует

осциллирующее слагаемое

| |

|

|

> 0,

> 0

| |

| |

| |

=

(−1)

| |

=

(−1)

.

Однако

в области

I

коэффициент

и

КФ

не изменяет знака.

Во второй области,

показанной

>

на рис.(3.3,)

оба корня положительны и КФ монотонно убывает.

На одной границе области II

= 0

авторегрессия имеет

первый порядок и

( ) = |

| .

138

На другой границе, где				характеристиче-
ское уравнение имеет кратный	корень		=	=		. В этом
		+4 = 0

случае выражение для КФ запишется в таком виде:

	( ) = (1+ |		|)			| |	,
где					2
		1 −
	=		4	.
В третьей	1+		4			рис. 3.3		кор-
	области

ни характеристического уравнения комплексные и КФ определяется по следующей формуле:

где

(

) =

| |

( |

|+ ),

=

−

;

= arccos

, =

1

2

)

;

= (1+

)/(1−

.

При этом графики КФ имеют вид синусоиды с экспоненциальным уменьшением амплитуды.

139

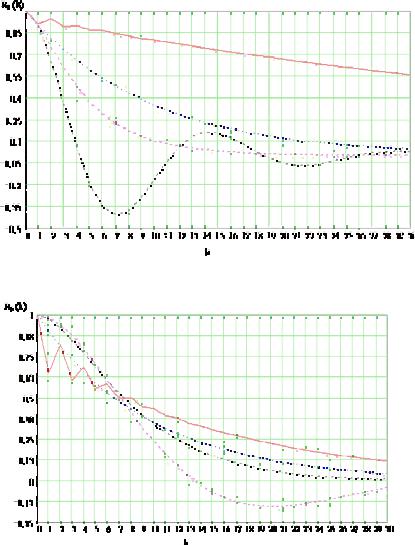
Рис. 3.4. Корреляционные функции при (1) = 0,9

Рис. 3.5. Корреляционные функции при (7) = 0,5

Для иллюстрации рассмотренных ситуаций на рис. 3.4 и рис. 3.5 представлены зависимости КФ ( ) при различных

140