Approximatsia

Аппроксимация функций. Метод наименьших квадратов.

Ранее были рассмотрены две задачи восстановления функциональных зависимостей: первая – вычисление значений трансцендентных функций, вторая – интерполяция. Решения обеих этих задач представлялись в виде алгебраического многочлена

. (1)

Исходными данными для определения коэффициентов многочлена в первом случае были значения производных разных порядков, заданных в какой-то одной точке, а во втором случае значения самой функции, заданные в нескольких точках.

При решении задачи аппроксимации также задаются значения функции в разных точках в виде таблицы x_j, y_j, j=1,…,m. Однако в этом случае считается, что значения функции содержат значительную долю случайной погрешности. Самих значений задается, как правило, больше, чем при решении задачи интерполяции (рис.1). Поэтому в результате решения задачи аппроксимации полученная функция может не пройти ни через одну из заданных точек. Она должна пройти между ними наилучшим (в каком-либо смысле) образом.

Очевидно, что решать задачу интерполяции в случае, рассмотренном на рис.1, не имеет смысла.

Рис. 1. К задаче аппроксимации функций

Переходим к математической постановке задачи. Для этого нужно математически определить критерий качества аппроксимации. Один из подходов к формированию критерия качества сводится к построению так называемой функции штрафа.

В начале необходимо решить, что является нарушением, которое может вызвать штрафование, и от чего зависит размер штрафа. Очевидно, что в данной задаче нарушением может быть непрохождение кривой, соответствующей аппроксимирующей функции, через одну из заданных точек. Причем, можно считать, что эти нарушения независимы, т.е. величины штрафов, накладываемые за каждое из нарушений в отдельности, не зависят друг от друга. Отсюда следует первый важный вывод, что функцию штрафа следует искать в виде суммы штрафов за каждое отдельное нарушение

.

Остается найти вид функции локального штрафа. Нужно решить от какого параметра зависит величина штрафа. На этот вопрос ответить легко, поскольку взаимное расположение кривой и точки удобнее всего характеризовать расстоянием по оси ординат, то есть .

Теперь перейдем к построению зависимости , т.е. локальных штрафов.

При этом необходимо учитывать два условия:

- задача, которая получится в результате нашего выбора, должна иметь достаточно простое решение;

- полученное решение должно быть разумным с общей точки зрения, (например, кривая не должна проходить вне всей группы точек и т.п.).

В связи с этим поиск подходящей функциональной зависимости следует начинать с наиболее простых. Самыми простыми являются зависимости вида y=const, y=x. Первая нас, очевидно, не устраивает. Попытаемся представить функцию локального штрафа в виде

. (2)

Проанализируем последствия этого выбора.

Во–первых, наличие абсолютной величины в зависимости (2) приводит к ее негладкости (разрыву первой производной). Поэтому для минимизации штрафа невозможно применять методы, основанные на поиске стационарных точек . Это серьезно усложняет задачу.

Во вторых, рассмотрим ситуацию, изображенную на рис.2. Одному и тому же значению x=x_i=x_j соответствуют разные значения y_i и y_j. Такая ситуация очень часто случается при проведении повторных экспериментов с целью уменьшения влияния случайной составляющей погрешности. В данном случае

.

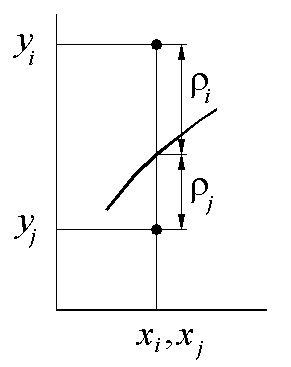
Рис. 2. Расположение кривой между точками

Таким образом, функция штрафа не зависит от положения кривой относительно этих двух точек. Мы пришли к некорректной задаче, что дополнительно осложняет ее решение. К тому же, исходя из здравого смысла, в этой ситуации наилучшим может быть только одно решение, когда кривая проходит точно посередине между двумя точками.

Значит, выбор следует отвергнуть.

Следующей по уровню сложности функциональной зависимостью является функция вида y=xx=x². Тогда

.

Данная функция является гладкой, и, следовательно, этот способ выбора _j(_j) не препятствует применению методов, связанных с дифференцированием.

Теперь найдем решение задачи в ситуации, показанной на рис.2.

,

где P – значение полинома .

Продифференцируем это выражение по P

.

Отсюда имеем: , что соответствует решению, которое было получено из соображений здравого смысла.

В результате этого анализа мы приходим к заключению, что данный выбор удовлетворяет нашим требованиям.

Теперь окончательно сформулируем задачу в виде метода наименьших квадратов: минимизировать функцию

.

При этом значение Ф зависит только от значений коэффициентов многочлена (1), то есть Ф=Ф(a₀,a₁,…,a_n). Тогда с учетом (1)

.

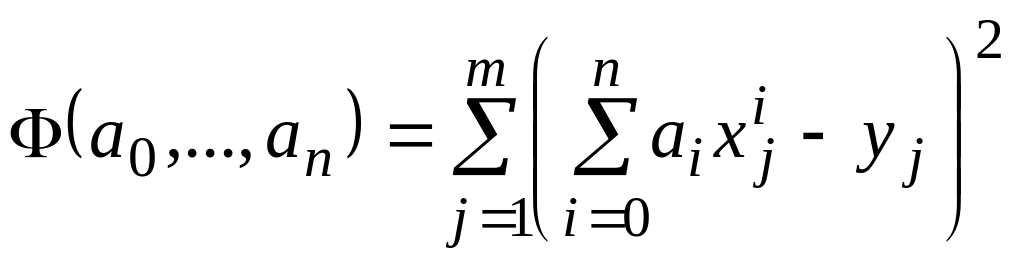Для минимизации этой функции необходимо найти решение системы уравнений

.

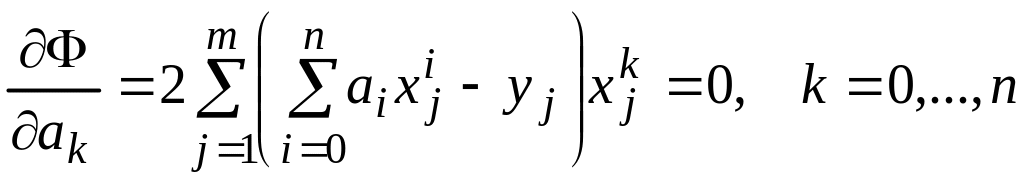Преобразуем это выражение

.

Эта система уравнений имеет вид

,

т. е. решение задачи методом наименьших квадратов сводится к решению системы линейных алгебраических уравнений.

Если число различных точек x_j m>n, то матрица системы не вырождена и решение системы существует и единственно. Это означает, что найденное решение доставляет функции Ф именно минимум, поскольку функция, имеющая вид суммы квадратов некоторых величин с положительными коэффициентами не может иметь единственной стационарной точки другого типа максимума.

При практическом применении метода наименьших квадратов степень многочлена n не следует выбирать слишком большой, так как это может привести к появлению осциллирующего характера у искомой функции P_n(x).

Поскольку, при постановке задачи предполагалось наличие значительной доли случайной погрешности (эта погрешность относится к погрешности исходных данных), то для оценки погрешности результата решения можно применить статистические способы, например, оценку среднеквадратичной погрешности .