1.Отличительные особенности предмета компьютерной математики. Ограниченность ресурсов. Классификация источников погрешностей. Особенности машинной арифметики: представление чисел в форме с фиксированной и плавающей запятой.

Ограниченность ресурсов. По времени, по памяти, возможностям вычислительным машин связана с тем, что существуют выдуманные математиками вещи, которые при реальном применении, оказываются не такими идеальными (например, пределы, интегралы). Абсолютно точных величин не может получиться, но все можно представить приближенно. Из-за этого мы теряем универсальность решений и получаем некоторую погрешность, но зато получаем возможность решать сложные задачи на имеющихся компьютерах.

Отличительные особенности предмета компьютерной математики. Предмет появился относительно недавно (около 50 лет назад), изучаются проблемы, связанные с особенностями вычисления с применением компьютеров. Решаем нерешаемые проблемы, на технике, которая для этого не приспособлена, в силу ограниченности возможностей.

Все результаты вычислительной математики приближенные, поэтому должны сопровождаться указанием диапазоны неопределенности (оценки погрешности).

Классификация источников погрешностей.

1)Погрешность математического моделирования.

Для решения задачи реальный объект или процесс упрощается, берутся только необходимые его свойства. Мат модель состоит из неких значений, формул, уравнений.

Мы не оцениваем эту погрешность, т.к. в рамках предмета работаем с уже созданными мат моделями.

2)Погрешность исходных данных.

Есть погрешности, связанные с точностью измерительного прибора, данные которого мы используем.

Особенности машинной арифметики. Если данные хранятся на компьютере, то погрешность связана с ограниченностью представления чисел, то есть ограниченность разрядности, в зависимости от разрядности последние цифры числа могут не уместиться. Такая погрешность не превышает единицу последнего разряда (либо единица, либо пол единицы последнего разряда).

В компьютере числа с плавающей точкой записываются в нормализованном виде: прямо после точки записывается старшая значащая цифра и это умножается на 10 в какой-то степени, то есть хранятся в компьютере, как знак числа, затем мантисса (т.е. количество разрядов), и порядок. В компьютере все это представлено в двоичной системе.

Относительная погрешность

.

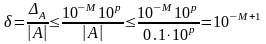3) Погрешность округления при выполнении арифметических операций.

При проведении операций на разноразрядных числах, происходит выравнивание порядков чисел по большему. Из-за этого разряды в конце меньшего числа могут потеряться. Погрешность так же не превышает единицу последнего разряда. При вычитании близких чисел после нормализации возникает погрешность, и так же если исходные числа уже имели некую погрешность.

Относительная погрешность

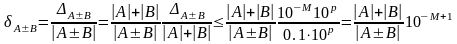
4) Погрешность численного метода.

Возникает при приближении самого метода (например при замене дифференцирования – отношением конечных разностей). В этом случае мы пытаемся задать условия таким образом, чтобы минимизировать погрешность, то есть чтобы погрешность была меньше заданной величины.

5) Погрешность, вызванная человеческим фактором.

При разработке программы, при внесении некоторых данных в код могут возникнуть ошибки, и вызванные ими погрешности никак нельзя оценить. Чтобы избежать такого, например, измеряют данные или решают задачу несколькими методами и сравнивают результаты. То есть мы снова отказываемся от абсолютной точности.

2.Математические модели погрешностей: случайная и предельная. Погрешности суммы, разности, произведения, частного. Интервальная арифметика.

Математические модели погрешностей: случайная и предельная. Существуют абсолютная погрешность- модуль разности точного значения и приближенного и относительная погрешность- отношение абсолютной к модулю самого числа.

Случайная модель предполагает, дельта x (т.е. абсолютная погрешность) случайная величина, и определяется вероятность возникновения абсолютной и относительной погрешностей.

Для арифметических операций получаются правила:

среднеквадратическая погрешность при сложении и вычитании (z=xy):

;

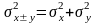среднеквадратическая погрешность при умножении и делении (z=xy; z=x/y): получается то же самое, только с относительными погрешностями.

.

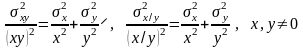Предельная погрешность предполагает самый худший вариант из возможных. (грубая оценка, которая гарантирует, что хуже этого точно не должно получиться) Определяется как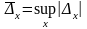 (супремум – верхняя возможная граница)

Если нам известно приближенное число и его предельная погрешность, полагается, что модуль разности приближенного числа и его точного значения не превышает предельной погрешности.

При сложении предельная погрешность суммы равна сумме предельных погрешностей взятых чисел.

Предельная погрешность произведения примерно равна модулю первого числа, умноженного на предельную погрешность второго и плюс, наоборот, модуль второго на погрешность первого.

3) При делении (z=x/y, 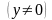), то что получилось бы при умножении чисел делим на модуль квадрата числа, на которое мы делим

.

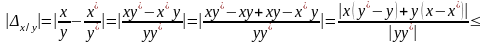
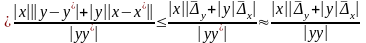Относительная погрешность произведения и деления равна сумме отдельных погрешностей чисел.

При возведении в целую степень относительная равна (справедливо тока для погрешностей значительно меньше 1):

.

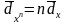Интервальная арифметика. Из-за того, что вычисление мат погрешностей было, скажем так, не очень удобным, возник подход, при котором переменные задаются интервалом, то есть для числа x-интервал от xmin до xmax.

Сумма чисел x и y принадлежит интервалу от суммы xmin и ymin, до суммы xmax ymax.

Для разности x и y – интервал от xmin-ymax до xmax-ymin.

Для произведения чисел из-за того, что границы могут быть разных знаков, принадлежит интервалу от минимума из возможных перемножений минимумов максимумов по x и y, и максимуму от таких же перемножений. То же самое для деления и возведения в целую степень.

Благодаря интервальной арифметике гарантируется, что результат вычислений будет входить в определенный интервал.

3.Вычисление значений многочлена. Схема Горнера. Вычисление значений трансцендентных функций.

Вычисление значений многочлена. Есть алгебраический многочлен 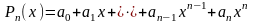, нам нужно вычислить его сумму при каком-то заданном значении x. Существуют разные способы: можно просто делать в лоб, высчитывая постепенно каждое слагаемое, получится много действий, можно при вычислении запоминать текущее значении x в некой степени, и потом просто домножать его на x (выполняется 2n умножений и n сложений). Это все трудоемко.

С помощью схема Горнера можно вычислить значение многочлена оптимальным способом, то есть минимизируется количество операций. Расставляются скобки и вычисления происходят, начиная с конца.

P_n(x)=a₀+x(a₁+x(a₂+…+x(a_n-1+xa_n)…)

Вычисление значений трансцендентных функций. Трансцендентные – это тригонометрические и обратные тригонометрические, гиперболические, показательные и логарифмические. Чтобы представить функцию в виде алгебраического многочлена, нужно найти коэффициенты многочлена, найти оценку погрешности (разницы между точным значением функции и полученным значением многочлена) и способ управления параметрами алгоритма (чтобы решение имело заданную точность).

С помощью формулы Тейлора можно представить функции типа sinx cosx. Если есть значение функции в какой-то точке и значения ее производных до n, то по формуле Тейлора мы можем найти значение функции в окрестностях этой точки

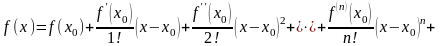
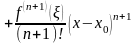, где  - некоторая точка, лежащая между x и x₀ при xx₀.

В разложении последнее слагаемое – это остаточный член формулы Тейлора в форме Лагранжа.

Если известна верхняя оценка модуля числителя в этом слагаемом, то, по сути само слагаемое будет являться оценкой погрешности, т.к. f(x)-точное значение, представленное разложение- это приближенное значение и последний член как раз представляет их разность, является абсолютной погрешностью.

Если при вычислениях использовать одинарную точность, можно получить ответ, в котором погрешность во много раз превосходит сам ответ. Из-за того, что аргумент большой, накапливается погрешность, чтобы этого избежать, например, для периодичных функций изменяют аргумент, т.е. прибавляют или вычитают значения периода (2pi,4pi..). Для всех функций разные приемы.

4.Интерполяция. Постановка задачи. Интерполяционный многочлен Лагранжа. Теоретическая и практическая оценка погрешности интерполяции. Сплайн-интерполяция. Алгоритм построения интерполяционного кубического сплайна. Оценка погрешности интерполяции сплайном.

Интерполяция. Постановка задачи. Некая функция задана дискретным множеством точек x, в них есть значения функции, то есть игреки. Нам нужно приближенно найти формулу функции, которая проходит через эти заданные точки, чтобы потом можно было вычислить значения в промежуточных точках (т.е. найти аналитический вид функции). Интерполирующую функцию ищут в виде алгебраического многочлена, нам при заданных условиях надо найти коэффициенты многочлена

Интерполяционный многочлен Лагранжа. Нужен для получения интерполирующей функции. Его структура такая: в заданных узловых точках он равен заданным значениям игриков, а в промежуточных там будут получаться некие значения. Можно выбрать степень этого многочлена в зависимости от того, какая точность нужна.

В форме интерполяционного многочлена Лагранжа представляется: сумма игриков умноженная на произведение дробей (x-xi)/(xj-xi)

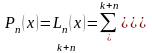
Теоретическая и практическая оценка погрешности интерполяции. Если интерполируем уже заданную определенную функцию, то оценка погрешности может быть задана аналитически (например, производная любого порядка от функций sinx и cosx по модулю не превышает единицы).

Есть формула, выведенная по формуле Тейлора, где точное значение функции равно приближенному значению в виде интерполяционного многочлена и погрешности, которая по сути является остаточным членом по формуле Тейлора

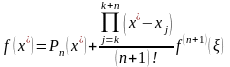
На практике функция нам не дана. Оценку интерполяции можно сделать с помощью рекуррентного соотношения Эйткена, по которой, зная 2 многочлена степени n, которые проходят через 2 набора точек, сдвинутые на единицу, получить многочлен на степень больше, который можно использовать вместо точного значения функции, чтобы оценить погрешность этих двух многочленов.

Если в предыдущей формулу для нахождения точного значения функции представляем производную, деленную на N+1 факториал, как букву С, то можно представить математическую модель погрешности интерполяции

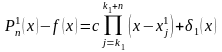
И в таком случае разница между приближенным и точным значением представляется как исходная формула, с замененной постоянной буквой С и еще некоторая малая погрешность (она возникает, когда при взятии формулы Тейлора ряд обрезался в конце).

По факту мы получаем уточненное значение функции через 2 полинома.

Сплайн-интерполяция. Нам задано дискретное множество точек X и значения Y в этих точках. В других методах мы через все имеющиеся точки проводим одну кривую, при интерполяции сплайном, на каждом отрезке будет своя функция. Сплайн – это функция, которая вместе с несколькими производными непрерывна на всём отрезке, на каждом отдельном отрезке задается алгебраическим многочленом.

Степень сплайна- максимальная степень многочленов среди всех отрезков.

Дефект сплайна- разность между степенью сплайна и порядком наивысшей производной, непрерывной на всем заданном отрезке.

На каждом отрезке кубический сплайн имеет вид S₃(x)=а_i0 +а_i1(x - x_i)+а_i2(x - x_i)² +а_i3(x - x_i)³ и в каждой узловой точке сплайн равен заданному значению игрика

Нам нужно найти коэффициенты аi, их будет 4n штук, для этого задаются 4n уравнений. Каждый многочлен должен проходить через начало и конец своего отрезка, это дает 2n уравнений, условие непрерывности первой и второй производных сплайна в внутреузловых точках дает 2n-2 уравнений, оставшиеся 2 уравнения добираются из краевых условий (ограничений на значение производных сплайна на концах промежутка).

Алгоритм построения интерполяционного кубического сплайна. Нам задано дискретное множество точек X и значения Y в этих точках, нам необходимо найти функцию в аналитическом виде, в случае сплайна это будет своя функция на каждом отрезке. У нас заданы условия, что сплайн непрерывен на всем отрезке вместе со своими производными до второго порядка включительно, каждый сплайн на концах отрезка равен соответствующим игрикам, а также сплайн удовлетворяет краевым условиям. Вторая производная сплайна непрерывна и линейна на каждом отрезке, ее задают в виде интерполяционного многочлена Лагранжа 1 степени:

, где m_i- вторая производная сплайна в точке xi

Потом чтобы найти значение функции, дважды интегрируем, у нас получается n-1 уравнений с неизвестными mi, mi-1, mi+1 в каждом. И найдя эти значения M, мы сможем найти сплайн на каждом отрезке.

Система уравнений задается трехдиагональной матрицей и мы используем метод прогонки для ее решения. Решение задается рекуррентной формулой m_i = _i m_i+1 + _i. На этапе прямой прогонки высчитываются прогоночные коэффициенты и расписываются зависимости M, на обратной по выведенной формуле, начиная с конца находим значения вторых производных. Из краевых условий мы знаем, чему равна Mn.

Оценка погрешности интерполяции сплайном. Находим середину каждого отрезка, в этих точках вычисляем разницу между значением сплайна и значением функции и находим максимум среди них.