ЭАиТЧ Бунина А.В. ПР 6 ИБ-01б

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное образовательное

учреждение высшего образования

«Юго-Западный государственный университет»

Практическая работа №6

По дисциплине «Элементы алгебры и теории чисел»

Вариант №6

Выполнил: Бунина А.В.

студент группы ИБ-01б

Проверил: Добрица В.П.

профессор

Курск, 2021

Задание 1. Решить сравнение методом подбора или прибавлением к правой части сравнения величины b + km, кратной a:

Заметим, что (12, 6) = 6, и 3 не делится на 6, а поэтому данное сравнение не имеет решений. (А где же здесь метод подбора? Какие числа надо проверять?)

Ответ: (12, 6) = 6, а 3 не делится на 6, то решение имеет единственное решение.

Используем аппарат цепных дробей. Разложим в цепную дробь число , получим:

Задание 2. Решить сравнение первой степени методом Эйлера. Правильность ответа проверить подстановкой:

Прежде всего, заметим, что (5,17) = 1, а поэтому данное сравнение имеет единственное решение.

Так как , то , а отсюда

(Вы уверены?) а так как , то , а поэтому

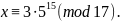
Так как , то

Возводя обе части в четвёртую степень, получим: (И это 4-я степень 6?) а так как , то , а поэтому

Следовательно, , т.е.

а отсюда, вычитая 17 из правой части сравнения, получим: 5¹⁵ ≡ 7(mod 17).

Тогда 3∙5¹⁵ ≡3∙7(mod 17), т.е. 3∙5¹⁵ ≡21(mod 17), а отсюда, вычитая 17 из правой части сравнения, получим: 3∙5¹⁵ ≡4(mod 17). Следовательно, x ≡ 4(mod 17).

Проверка: 5∙4 = 20 = 17∙1 + 3, т.е. 5∙4 ≡ 3(mod 17).

Исправление:

Прежде всего, заметим, что (5,17) = 1, а поэтому данное сравнение имеет единственное решение.

Так как , то , а отсюда

(Вы уверены?) а так как , то , а поэтому

Так как , то

Возводя обе части в четвёртую степень, получим: а так как , то , а поэтому

Следовательно, , т.е.

а отсюда, вычитая 17 из правой части сравнения, получим: 5¹⁵ ≡ 7(mod 17).

Тогда 3∙5¹⁵ ≡3∙7(mod 17), т.е. 3∙5¹⁵ ≡21(mod 17), а отсюда, вычитая 17 из правой части сравнения, получим: 3∙5¹⁵ ≡4(mod 17). Следовательно, x ≡ 4(mod 17).

Проверка: 5∙4 = 20 = 17∙1 + 3, т.е. 5∙4 ≡ 3(mod 17).

Задание 3. Решить сравнение разложением в цепную дробь:

Вычитая из правой части 201, получим равносильное сравнение 69x ≡ 192(mod 201).

Прежде всего, заметим, что (69, 192) = 3, и 201 делится на 3, а поэтому данное сравнение имеет три решения.

Разделим обе части сравнения и модуль на 3. Тогда получим сравнение

Разложим в цепную дробь.

Применяя к числам 67 и 23 алгоритм Евклида, получим:

	q0 = 2
	q1 = 1
	q2 = 10
	q3 = 2

Составим соответствующую таблицу для нахождения числителей подходящих дробей

k		0	1	2	3
qk		2	1	10	2
Pk	1	2	3	32	67

Так как n = 3, то P_n–1 = P₂ = 32.

Решение сравнения по методу непрерывных дробей записывается в виде

Следовательно,

Отсюда x ≡ –38 (mod 67) или x ≡ 29 (mod 67) (Приведите подробные рассуждения.)

Числитель предпоследней подходящей дроби равен P_n–1 = P₂ = 32, тогда по формуле:  , то есть 

Тогда все решения исходного сравнения по модулю 201 будут иметь вид:

, где k = 0, 1, 2, т.е. (Почему эти k?)

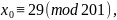
(Сделайте проверку.)