
ЛР_1
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное образовательное
учреждение высшего образования
«Юго-Западный государственный университет»
Лабораторная работа №1
По дисциплине «Математическая логика и теория алгоритмов»
Вариант №5
Выполнил: Бунина А.В.
студент группы ИБ-01б
Проверил: Добрица В.П.
профессор
Курск, 2021
Задача 1. Определите, является ли данное выражение формулой. Если это формула, то выпишите последовательность построения формулы.

Решение:
Понятие формулы алгебры высказываний в математической логике определяется следующим образом:
‒ пропозициональная переменная является формулой;
(пропозициональная переменная – переменная для высказываний, область значений которой состоит из двух т. н. истинностных значений: «истина» и «ложь»);
‒ если А и В ‒ формулы, то (А & В), (А В), (¬А), (А В), (АВ), (А В), (А В), (А В) ‒ формулы;
‒ других формул, кроме построенных выше конечным числом их применений, нет.
Допускается
запись:
 .
.
Последовательность построения формулы:

Х
У
Z
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
1
1
1
1
1
|
Z |
|
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
(А таблицы истинности можно было и не заполнять.)
Последовательность построения формулы:
Задача 2. Сколькими способами можно расставить скобки в последовательности, чтобы получилась формула. Выписать все возможные получаемые формулы.

Расставить скобки в последовательности можно 3 способами:
(Вообще то для оценки можно применить комбинаторику. И тогда оценка 3!=6.)
 (Это
не формула.)
(Это
не формула.)(Это не формула.)
 (Это
не формула.)
(Это
не формула.)

 (Чем
отличается от 3?)
– выделена формула
(Чем
отличается от 3?)
– выделена формула
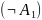 .
. (Это
не формула.)
(Это
не формула.)

- я не знаю.
Задача 3. Выписать все подформулы данной формулы.

В
формуле
 одиннадцать
подформул:
одиннадцать
подформул:
 ,
, ,
А,
В, С, D,
,
А,
В, С, D,
 ,
,
 ,
,
 ,
,
 и
сама формула, которая является
несобственной подформулой. Первые 10
являются собственными подформулами.
(Расположите
в соответствии с ростом сложности,
указывая ее.)
и
сама формула, которая является
несобственной подформулой. Первые 10
являются собственными подформулами.
(Расположите
в соответствии с ростом сложности,
указывая ее.)
1)А, В, С, D – сл. 0
 ,
– сл. 1
,
– сл. 1
3) – сл. 2 (Вы уверены? Посмотрите внимательно определение.)
4) – сл. 3
5) – сл. 2
6) – сл. 3
сама формула, которая является несобственной подформулой. – сл. 4
В
результате: А,
В, С, D,
,
,
,
 ,
,
.
,
,
.
Под сложностью формулы понимается число, характеризующее число этапов построения формулы. Сложность формулы равна максимальной сложности собственных подформул, увеличенная на 1. Простые высказывания имеют сложность 0.
1)А, В, С, D – сл. 0
, – сл. 1
3) – сл. 1
4) – сл. 2
5) – сл. 2
6) – сл. 3
сама формула, которая является несобственной подформулой. – сл. 4
Задача 4. Указать тип формулы. Доказать вывод.

Для формулы составим таблицу истинности, с помощью которой и определим тип формулы.
A |
B |
C |
D |
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Так как у формулы есть значение 0, то она не является тождественно истинной. А так как есть значения 1, то она является выполнимой. Существуют еще тождественно ложный тип формулы. (И не только.)
Опровержимые – ложные при некотором наборе значений аргументов.
Задача 5. С помощью таблиц истинности, а также с помощью эквивалентных преобразований проверить на эквивалентность формулы.
|
|
||||||
A |
B |
C |
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
A |
B |
C |
|
|
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
Формулы принимают значение 0 на разных наборах значений переменных, поэтому они не эквивалентны.
Применим эквивалентное преобразование, заменив импликацию через отрицание и дизъюнкцию.

(Для проверки эквивалентности с помощью эквивалентных преобразований необходимо формулы привести к совершенной форме либо СДНФ, либо к СКНФ. Вид совершенной формы однозначный с точностью до порядка записи. Поэтому проверка эквивалентности становится тривиальной.)
 СДНФ:
СДНФ:

СКНФ:

СДНФ:


СКНФ:

По таблицам истинности и по эквивалентным преобразованиям F1 и F2 мы видим, что данные формулы не являются эквивалентными.
Задача 6. Представьте логическими формулами пословицы и поговорки.
Когда грома много – дождя мало.
В поговорке «Когда грома много – дождя мало.» выделим простые высказывания, обозначив из буквами: А- много грома, В – много дождя. Тогда пословица примет вид (А → ¬B).
Задача 7. Доказать законы логики.
Ассоциативность дизъюнкции. Закон поглощения для конъюнкции.
Ассоциативность дизъюнкции:
A |
B |
C |
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Закон поглощения для конъюнкции:
А |
В |
|
|
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Задача 8. При каких значениях переменных формула ложна.
X |
Y |
|
|
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Формула будет ложна при значениях переменных X=0, Y=1.
Импликация ложна только в случае истинности посылки и ложности заключения. Следовательно, 𝑋 = 0, но при этом посылка будет истинной только при Y = 1. В данном случае это единственный набор, на котором формула ложна.























