
ЛР1 / MO_LR1
.docxЛабораторная работа №1
Климашин Денис, ИВТ-12М
Вариант 10
1)
Метод
перебора

Метод
поразрядного поиска

Метод
дихотомии

Метод
золотого сечения

Метод
парабол

Метод
средней точки
Метод
хорд

Метод
Ньютона
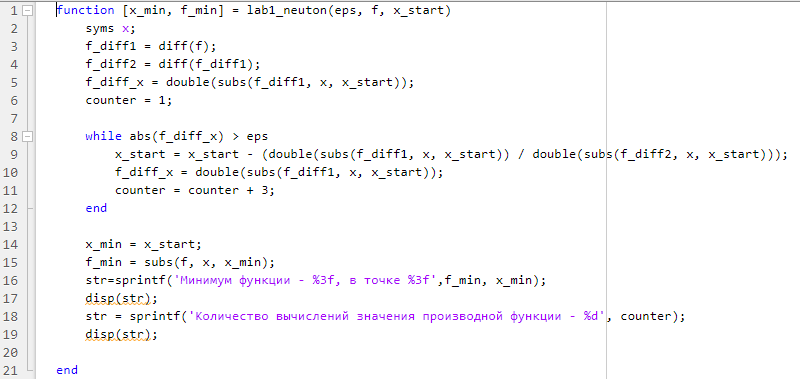
2)
f(x) = x3 – 3sin(x), x ∈ [0; 1]

3)
Метод |
Точность |
xmin |
fmin |
Кол-во вычислений |
Перебора |
0.01 |
0.820000 |
-1.642069 |
101 |
Перебора |
0.001 |
0.824000 |
-1.642130 |
1001 |
Перебора |
0.0001 |
0.824100 |
-1.642130 |
10001 |
Перебора |
0.00001 |
0.824130 |
-1.642130 |
100001 |
Поразрядного поиска |
0.01 |
0.820312 |
-1.642130 |
21 |
Поразрядного поиска |
0.001 |
0.825195 |
-1.642130 |
26 |
Поразрядного поиска |
0.0001 |
0.824219 |
-1.642130 |
35 |
Поразрядного поиска |
0.00001 |
0.824135 |
-1.642130 |
48 |
Дихотомии |
0.01 |
0.819672 |
-1.642059 |
12 |
Дихотомии |
0.001 |
0.823666 |
-1.642130 |
20 |
Дихотомии |
0.0001 |
0.824151 |
-1.642130 |
26 |
Дихотомии |
0.00001 |
0.824134 |
-1.642130 |
32 |
Золотого сечения |
0.01 |
0.826238 |
-1.642115 |
11 |
Золотого сечения |
0.001 |
0.823725 |
-1.642130 |
15 |
Золотого сечения |
0.0001 |
0.824145 |
-1.642130 |
20 |
Золотого сечения |
0.00001 |
0.824133 |
-1.642130 |
25 |
Парабол(0.3, 0.8, 1) |
0.01 |
0.823095 |
-1.642127 |
5 |
Парабол(0.3, 0.8, 1) |
0.001 |
0.823770 |
-1.642130 |
6 |
Парабол(0.3, 0.8, 1) |
0.0001 |
0.824120 |
-1.642130 |
8 |
Парабол(0.3, 0.8, 1) |
0.00001 |
0.824132 |
-1.642130 |
10 |
Средней точки |
0.01 |
0.824219 |
-1.642130 |
8 |
Средней точки |
0.001 |
0.824219 |
-1.642130 |
8 |
Средней точки |
0.0001 |
0.824127 |
-1.642130 |
15 |
Средней точки |
0.00001 |
0.824131 |
-1.642130 |
18 |
Хорд |
0.01 |
0.822932 |
-1.642125 |
5 |
Хорд |
0.001 |
0.824026 |
-1.642130 |
6 |
Хорд |
0.0001 |
0.824123 |
-1.642130 |
7 |
Хорд |
0.00001 |
0.824131 |
-1.642130 |
8 |
Ньютона(x0 = 0.5) |
0.01 |
0.824146 |
-1.642130 |
10 |
Ньютона(x0 = 0.5) |
0.001 |
0.824146 |
-1.642130 |
10 |
Ньютона(x0 = 0.5) |
0.0001 |
0.824146 |
-1.642130 |
10 |
Ньютона(x0 = 0.5) |
0.00001 |
0.824132 |
-1.642130 |
13 |
Выводы: 1. Среди методов, использующих значения функции в точке, самый простой (метод перебора) оказался самым неэффективным, количество вычислений значения функции N зависит обратно пропорционально от точности ε. Улучшенный вариант этого метода (метод поразрядного поиска) является намного эффективней, в силу использования унимодальности исследуемой функции. 2. Для методов с исключением отрезков можно рассмотреть формулы для вычисления количества итераций, зависящих от точности. Для метода дихотомии фигурирует log2(x), который растёт быстрее чем ln(x), используемый для метода золотого сечения. Соответственно, для второго метода требуется меньшее кол-во итераций, а значит и меньшее кол-во вычислений значения функции в точке, что и видно из результатов. 3. Метод парабол является наиболее эффективным среди прямых методов, так как в этом методе строится аппроксимирующий многочлен второго порядка с дальнейшим уменьшением отрезка аппроксимации. 4. Сравнивая метод средней точки и метод дихотомии, можно сделать вывод, что первый является почти в два раза эффективней второго метода, так как вычисление двух значений функции вблизи середины очередного отрезка в методе дихотомии можно заменить вычислением одного значения производной исследуемой функции. 5. Рассматривая метод Ньютона можно заметить, что для минимизации исследуемой функции с точностью 0.01, 0.001 и 0.0001 потребовалось одинаковое количество вычислений, что говорит о квадратичной скорости сходимости последовательности.
4)
f(x) = x*arctg(x) – 0.5*ln(1+x2)

Начальное приближение |
x_min |
f_min |
0 |
0 |
0 |
1 |
0 |
0 |
-1 |
0 |
0 |
1.3 |
-0.000026 |
0 |
-1.3 |
0.000026 |
0 |
1.4 |
Расходится |
Расходится |
-1.4 |
Расходится |
Расходится |
Диапазон начального приближения, при котором последовательность будет сходиться: x <=|1.39174|.
Метод
Ньютона-Рафсона

Начальное приближение |
x_min |
f_min |
0 |
0 |
0 |
1 |
0.000546 |
0 |
-1 |
-0.000546 |
0 |
2 |
-0.000008 |
0 |
3 |
0.000883 |
0 |
4 |
Расходится |
Расходится |
Диапазон начального приближения, при котором последовательность будет сходиться: x <=|3.37072|.
Метод Марквардта
(µ0=5)

Начальное приближение |
x_min |
f_min |
0 |
0 |
0 |
5 |
-0.000750 |
0 |
10 |
0.000048 |
0 |
20 |
0.000377 |
0 |
30 |
0.000296 |
0 |
40 |
Расходится |
Расходится |
Диапазон начального приближения, при котором последовательность будет сходиться: x <=|39.87|.
Выводы: 1. Можно использовать обычный метод Ньютона для минимизации исследуемой функции, но для этого нужно предварительно рассчитать диапазон для начального приближения, иначе последовательность может расходиться. 2. Метод Ньютона-Рафсона позволяет расширить диапазон для начального приближения при помощи более сложного расчёта новой точки, что требует большего количества вычисления значений производной функции в точке.
5)

f(x) = cos(x)/x2, x ∈ [1; 12], L = 1.91

Метод перебора
Точность eps |
x_min |
f_min |
Кол-во вычислений функции |
0.01 |
2.460000 |
-0.128325 |
1101 |
0.001 |
2.459000 |
-0.128325 |
11001 |
0.0001 |
2.458700 |
-0.128325 |
110001 |
0.00001 |
2.458710 |
-0.128325 |
1100001 |
Метод ломанных
Точность eps |
x_min |
f_min |
Кол-во вычислений функции |
0.01 |
2.460292 |
-0.128325 |
216 |
0.001 |
2.458165 |
-0.128325 |
652 |
0.0001 |
2.458659 |
-0.128325 |
1694 |
0.00001 |
2.458702 |
-0.128325 |
4648 |
f(x) = 0.1x+2sin(4x), x ∈ [0; 4], L = 8.1

Метод перебора
Точность eps |
x_min |
f_min |
Кол-во вычислений функции |
0.01 |
1.170000 |
-1.881951 |
1101 |
0.001 |
1.175000 |
-1.882347 |
11001 |
0.0001 |
1.175000 |
-1.882347 |
110001 |
0.00001 |
1.174970 |
-1.882347 |
1100001 |
Метод ломанных
Точность eps |
x_min |
f_min |
Кол-во вычислений функции |
0.01 |
1.175515 |
-1.882342 |
90 |
0.001 |
1.174866 |
-1.882346 |
190 |
0.0001 |
1.174970 |
-1.882347 |
470 |
0.00001 |
1.174971 |
-1.882347 |
1798 |
