ЛР2 / MO_LR2

Лабораторная работа №2

Климашин Денис, ИВТ-12М

Вариант 1

Задание 1.

Метод наискорейшего спуска.

Метод сопряженных градиентов

Метод Ньютона

Метод регулярного симплекса

Метод циклического покоординатного спуска

Метод Хука-Дживса

Задание 2.

Метод	Коэффициент а	Точность	Кол-во вычислений	Кол-во итераций
Наискорейшего спуска	1	0.001	61	1
		0.00001	61	1
	250	0.001	300	5
		0.00001	421	7
	1000	0.001	2560	43
		0.00001	2927	49
Сопряженных градиентов	1	0.001	63	1
		0.00001	63	1
	250	0.001	312	5
		0.00001	438	7
	1000	0.001	565	9
		0.00001	692	11
Ньютона	1	0.001	2	1
		0.00001	2	1
	250	0.001	2	1
		0.00001	2	1
	1000	0.001	2	1
		0.00001	2	1
Правильного симплекса	1	0.001	738	81
		0.00001	1259	139
	250	0.001	7968	959
		0.00001	19877	2405
	1000	0.001	17706	2145
		0.00001	65381	7955
Циклического покоординатного спуска	1	0.001	380	6
		0.00001	380	6
	250	0.001	380	6
		0.00001	380	6
	1000	0.001	390	6
		0.00001	390	6
Хука-Дживса	1	0.001	17	3
		0.00001	25	5
	250	0.001	17	3
		0.00001	25	5
	1000	0.001	17	3
		0.00001	25	5

Выводы: градиентные методы примерно одинаково показали себя при минимизации функции данного вида, но при сильно овражной функции (коэффициент а=1000) метод сопряженных градиентов показал себя более эффективным, так как он избегает зигзагообразного характера приближения к точке минимума (выбор направления шага учитывает не только антиградиент, но и направление на предыдущем шаге). Метод Ньютона показал себя наиболее эффективным и сходился к точке минимума за одну итерацию, но это лишь из-за того, что это семейство функций является квадратичным (при минимизации функции от большего количества переменных вся вычислительная мощность лежала бы на вычислении обратного Гессиана). Метод регулярного симплекса очень неэффективен для минимизации сильно овражных функций, так как быстро опускается на «дно», а затем начинает медленно сходиться к минимуму. Остальные прямые методы минимизации показали себя стабильными для данного семейства функций.

Задание 3-4.

f(x) = 64x₁²+126x₁x₂+64x₂²-10x₁+30x₂+13

Метод	Точность	Итерации п.3	Вычисл. п.3	Итерации п.2	Вычисл. п.2
Наискорейшего спуска	0.001	372	20229	5	300
	0.00001	435	22889	7	421
Сопряженных градиентов	0.001	3	172	5	312
	0.00001	14	558	7	438
Ньютона	0.001	1	2	1	2
	0.00001	1	2	1	2
Правильного симплекса	0.001	99	882	959	7968
	0.00001	157	1403	2405	19877
Циклического покоординатного спуска	0.001	326	19164	6	380
	0.00001	472	27683	6	ё380
Хука-Дживса	0.001	3	198	3	17
	0.00001	5	321	5	25

Выводы:

1. Среди градиентных методов метод сопряженных градиентов показал на примере функции из п.3, что, избегая зигзагообразной траектории приближения к минимуму исследуемой функции, достичь минимума можно намного быстрее.

2. Метод Ньютона всё так же сходится к минимуму за одну итерацию, так как исследуемая функция квадратичная, вся вычислительная мощность заключается в вычислении обратного Гессиана, что сказалось бы на времени минимизации функции большего кол-ва переменных.

3. Для функции из п.3 метод регулярного симплекса срабатывает более быстро, так как в этом случае исследуемая функция не на столько овражна, как функция в п.2.

4. Циклический покоординатный спуск для функции из п.3 сходится медленнее к решению, так как данная функция не сепарабельна в отличии от функции из п.2.

5. Метод Хука-Дживса для функции из п.3 сходится за то же кол-во итераций, но с большим числом вычислений. Скорее всего это число вычислений лежит в основе предварительного этапа исследующего поиска.

Задание 5.

Табличка для методов, у которых есть одномерный поиск.

Метод	Точность алгоритма	Точность одномерного поиска	Кол-во вычислений	Кол-во итераций
Наискорейшего спуска	10-3	10-6	36535	709
		10-8	285653	4187
	10-5	10-6	36535	709
		10-8	515092	7745
Сопряженных градиентов	10-3	10-6	912	17
		10-8	1075	15
	10-5	10-6	1835	35
		10-8	1075	15
Циклического покоординатного спуска	10-3	10-6	6141	130
		10-8	8728	130
	10-5	10-6	65291	1364
		10-8	92976	1368

Выводы:

1. Метод циклического покоординатного спуска не позволяет при заданной точности получить точку минимума вследствие преждевременного окончания процесса поиска. Так для точности 10^-3 минимизация дала неправильный результат: точку (0.62, 0.38). А для точности 10^-5 минимизация дала близкий к истине результат: точку (0.95, 0.91).

2. Метод сопряженных градиентов сходится быстрее к точке минимума при большей точности одномерной минимизации. Так при решении задачи одномерной минимизации с точностью 10^-8 метод сошёлся за меньшее число итераций чем при решении той же задачи одномерной минимизации с точностью 10^-6.

3. Скорость метода наискорейшего спуска показалась очень чувствительной к точности решения задачи одномерной минимизации.

Табличка для методов, у которых нет одномерного поиска.

Метод	Точность	Кол-во вычислений	Кол-во итераций
Ньютона	10-3	2	1
	10-5	2	1
Регулярного симплекса	10-3	2712	336
	10-5	111083	16374
Хука-Дживса	10-3	120	3
	10-5	326	5

Задание 6.

Метод	Начальное приближение	Кол-во вычислений	Кол-во итераций	Точка минимума
Наискорейшего спуска	(0; 0)	748	13	(3;2)
	(-5; 0)	516	9	(3.6; -1.85)
Сопряженных градиентов	(0; 0)	641	11	(3;2)
	(-5; 0)	298	5	(3.6; -1.85)

Вычисления производились с точностью 10^-3, для решения одномерной минимизации была взята точность 10^-7.

Выводы:

При начальном приближении (0; 0) градиентные методы начинают спускаться в сторону возрастания аргумента x2, так как функция убывает в ту сторону, поэтому методы сходятся к точке минимума (3;2). А при начальном приближении (-5;0) функция убывает в сторону убывания аргумента x2, поэтому градиентные методы там сходятся к точке минимума (3.6; -1.85). То есть при минимизации многомодальных функций градиентные методы будут сходится к той точке минимума, к которой ближе спустились на первой итерации.

Начальное приближение (0;0)->сходимся к точке(3;2)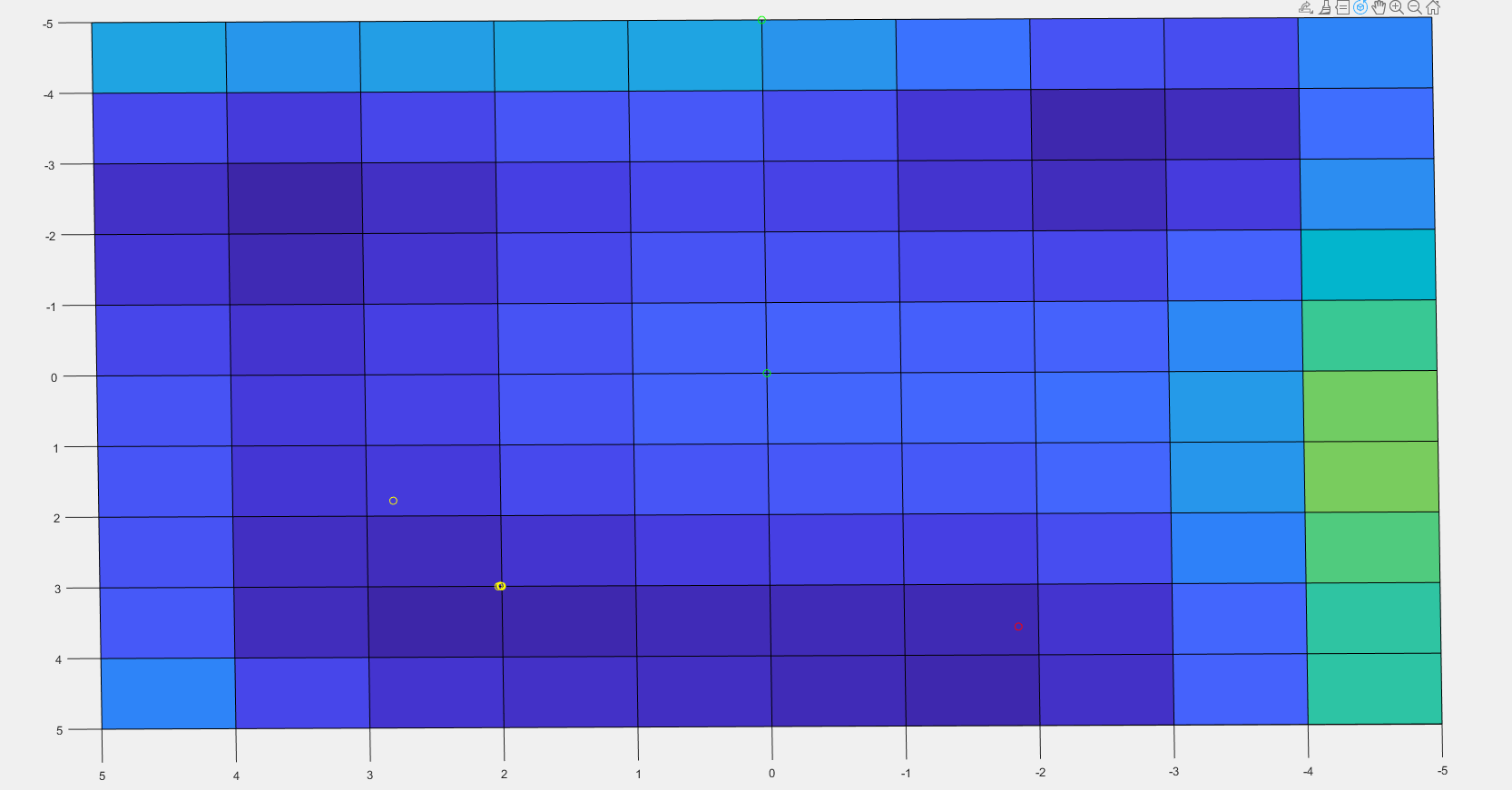

Начальное приближение (-5; 0)->сходимся к точке(3.6; -1.85)