2 курс ОАУ(ТАУ) [препод. Петунин В.И.] / Лекции / 7 (1)

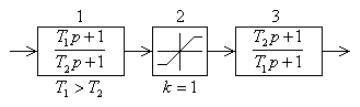
– соответственно инерционным звеном, т. е. фильтром нижних частот. Для малых входных сигналов, когда нелинейное звено 2 не входит в насыщение, передаточная функция всей схемы равна 1, т. е. это звено не влияет на работу системы, в которой находится. При достаточно больших сигналах, когда звено 2 входит в насыщение, схема ведет себя как динамическое звено со спадающей с ростом частоты амплитудной частотной характеристикой, степень спада которой зависит от величины входного сигнала, и с примерно постоянным фазовым сдвигом.

Рис. 7.10. Структурная схема нелинейного динамического корректирующего звена

Такое корректирующее звено применяется в качестве последовательного корректирующего звена, например, для устранения автоколебаний при больших возмущениях и соответствующего увеличения критического по устойчивости значения коэффициента передачи системы. Это корректирующее звено применяется также в цепях обратной связи, например, следящих систем для улучшения качества переходных процессов при больших входных сигналах.

Задачи нелинейной коррекции могут заключаться, как обычно, в достижении желаемых свойств процессов управления, причем должна предусматриваться возможность изменения этих свойств с изменением величины отклонения. Таким образом, открывается возможность преодолевать известное из линейной теории противоречие между требованиями точности и требованиями устойчивости системы, а также значительно усиливать регулирующее воздействие при больших отклонениях и т. п.

Кроме того, если в заданной нелинейной системе имеются вредные для процесса нелинейности (люфт, гистерезис, зона нечувствительности), то путем введения специальной нелинейной коррекции можно в известной мере ослабить вредное влияние

173

имеющихся в системе неизбежных нелинейностей.

В качестве первых примеров рассмотрим введение нелинейного корректирующего устройства в линейную систему.

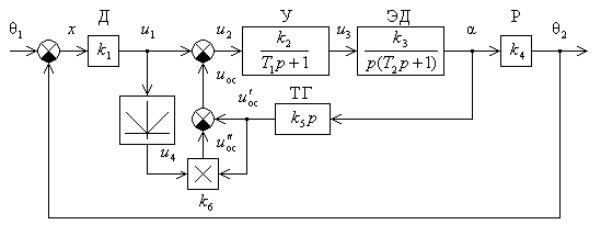
Пример 7.2. Проанализируем систему с нелинейной обратной связью, сигнал которой уменьшается с возрастанием ошибки. Схема такой системы показана на рис. 7.11.

Рис. 7.11

Решение. Напряжение, пропорциональное модулю ошибки, подается на вход умножителя и затем вычитается из выходного напряжения тахогенератора, находящегося в цепи линейной обратной связи. Сигнал обратной связи уменьшается, когда ошибка возрастает, что приводит к убыстрению отработки больших отклонений и уменьшению скорости отработки в конце процесса. Динамика системы описывается уравнениями

Уравнение

воздействия	1
	(θ

x = θ	− θ	2	,	u	= k x,	u	2	= u	− u	ос	,
1				1	1			1

(T1 p +1)u3 =k 2u2 , (T2 p +1) pα =k3u3,

	θ	2	= k	α, u = u			− u		,
			4		ос	ос	ос
u	= k pα,			u	= k u u		, u	4		=| u | .
ос	5			ос	6	4 ос				1

системы в переходном процессе без внешнего

= 0)	имеет вид

[T T

p

3

+ (T

+ T

) p

2

+ (1

+ k

) p + k ]x − k

ос

1 2

1

2

ос

где

kос = k2k3k5,

= k1k6kос ,

k = k1k2k4 .

kос

линеаризация входящей сюда нелинейности переходного процесса дает

| x | px = 0	,	(7.10)
Гармоническая
F (x) =| x | px		для

174

	F (x) =		q(a) + q (a)

где для данной нелинейности имеем

p − ω

ξ

 

x1

,

(7.11)

q(a) = q (a) =

1 πα

1 πα

2π

| a sin ψ |(aω cos ψ + aξ sin

0

2π

| a sin ψ |(aω cos ψ + aξ sin

0

ψ)

ψ)

sin ψdψ ,

cos ψdψ .

После интегрирования получаем

	q =	8	aξ,	q		=	4	aω .
		3π					3π

Тогда характеристическое уравнение системы

T T λ	3	+ (T	+ T		)λ	2	+ (1	+ k		)λ + k + k	4a
									ос
1 2		1	2							ос	3π
Подстановка λ = ξ +				jω		дает два уравнения

(7.10)

(λ + ξ)

примет вид

= 0 . (7.12)

T T ξ	3	+ (T	+ T	)ξ	2	+ (1 + k
							ос
1 2		1	2
						− (T + T
						1	2

− 3T T ω				2	−	8	k	α)ξ + k −
		1 2				3π	ос
)ω	2	= 0	;

3T T ξ	2	ω + 2(T	+ T	)ξω + (1 + k		−	4	k	α −T T ω	2	)ω
					ос
1 2		1	2				3π	ос	1 2

Из второго уравнения

	2		2		T + T			1 + k		ос		4k
ω		= 3ξ		+ 2	1	2	ξ				−	ос	,
					T T
								T T				3πT T
					1	2		1	2			1	2

=

0

.

а из первого –

a =			3π							4T1T2ξ3	+ 4(T1 + T2 )ξ2 +
				T			+ T
	2k		ξ +			1	2
	ос					T T
							1 2				T + T
				(T + T				)	2
			+			1	2			ξ − k +	1	2	(1	+ kос )
						T T					T T
							1 2				1	2

(1 + kос )ξ +

.

Ha основании этих двух формул можно построить диаграммы качества нелинейных переходных процессов по любому параметру,

например по параметру

k . Можно также при всех заданных

параметрах определить зависимости ξ(a) и ω(a) и произвести оценки качества переходных процессов.

175

Пример 7.3. Приведем пример введения нелинейной коррекции в нелинейную автоматическую систему. Схема системы представлена на рис. 7.12.

Рис. 7.12

Система имеет релейное управление. В качестве корректирующего устройства введена нелинейная обратная связь по скорости с параболической характеристикой

uос = kос x

2

sign x,

x = pβ .

Решение. После гармонической линеаризации имеем

u

= q (a

)x, q =

8

k

a

,

ос

ос

x

ос

3π

ос

x

где

ax

– амплитуда колебаний скорости

x = pβ .

характеристика

0

при

| u | b,

u2

=

при

| u | b

c sign u

в результате гармонической линеаризации принимает вид

		4c	b		2
u2 = q(a)u,					,
	q(a) =	πa	1 −
			a

(7.13)

Релейная

(7.14)

где а – амплитуда колебаний переменной u . Передаточные функции линейных звеньев системы указаны на схеме рис. 7.14.

Характеристическое уравнение гармонически линеаризованной системы получает вид

T1T2λ3 + (T1 + T2 )λ2 + [k2q(a)qос (ax ) +1]λ + k1k2k3k4q(a) = 0 . (7.15)

Выразим амплитуду ax через a . Согласно схеме рис. 7.13 получаем

176

ax =			k2q(a)					a .
		(1 − T T 2 )2		+ (T +T )2
						ω2
1			2	1	2

Тогда по формуле (7.13) получаем

q		=		8k		ос		k	2	a
	ос
					2			2				2		2
		3π	(1 − T T				)		+ (T +T		)		ω
			1	2						1	2

q(a)

.

(7.16)

Исследуем устойчивость данной системы с нелинейной обратной связью и сравним со случаем, когда в той же релейной

системе обратная связь линейна, т. е. когда величина

qос

заменяется

просто коэффициентом

kос . Границу устойчивости будем искать как

границу области существования автоколебаний.

Подставив в характеристическое уравнение (7.15)

λ = jω ,

получим

X = k k

k

q(a) − (T + T )ω

2

= 0,

2

3

1

1

2

(7.17)

Y = [k

2

q(a)q

ос

(a

x

) +1]ω − T T ω3 = 0.

1

2

Эти два уравнения с подстановкой (7.16) определяют частоту ω

и амплитуду

a

автоколебаний.

Выполнение

равенств

(7.17)

соответствует прохождению кривой Михайлова (при данном значении a ) через начало координат (кривая 1 на рис. 7.13).

Рис. 7.13

Для устойчивости системы (отсутствие автоколебаний) нужно,

однако, чтобы уравнения (7.17) не удовлетворялись и кривая Михайлова охватывала бы начало координат (кривая 2 на рис. 7.13),

т. е. чтобы при X = 0 выполнялось условие Y0 (a) 0 при любом значении a . Удобнее пользоваться выражением

177

Y0 (a)

Поскольку параметр ω 0, можно записать в виде

				Y
				0
Из условия	X = 0	, согласно
величину a :
		ω	2	=

=	Y0 (a)				.
		ω
то			данное			условие устойчивости
(a) 0 .							(7.18)
(7.17), выразим параметр ω							через
k k		2	k	3
1					q(a)		(7.19)
T + T
1				2

и подставим его в выражение для

Y

(a)

, используя одновременно и

подстановку (7.16). В результате получим условие устойчивости

(7.18) в виде

где

f

	Y		=
	0
(a) =			−
	1

8k		k		2		2						T T
	ос			2
					aq		(a) +1 −						1 2
3πf (a)												T	+ T
												1	2
T T											2
					k k		k		q(a)			+ (T +
1 2						2		3
T + T					1								1
1			2

k k	2	k	3	q(a)
1

T	)T T k k
2	1	2	1

2	k

0

,

3	q(a)

.

(7.20)

В случае, линейна, т. е.

если в

q	= k	ос
ос

данной релейной системе	обратная связь
, получим согласно (7.17)	более простое

выражение условия устойчивости

Y0

или

= k	2	k	ос	q(a)

		T T
	1 −	1	2
		T + T
		1	2

+1 −

k k	3
1

T T
1	2	k k	2	k	3	q
T + T		1
1	2

− k			q(a)
	k	2
	ос

(a)

0.

0

,

(7.21)

Отсюда видно, что если

	kос	T1T2		k1k3	,	(7.22)
		T1	+ T2

то система устойчива при любых значениях коэффициента усиления k2 и сигнала с реле.

При

	kос	T1T2	k1k3
		T1 + T2
	условие (7.21) будет удовлетворено		при всех значениях a в том

178

случае, если оно удовлетворяется при наибольшем значения

q

.

График

q(a)

, согласно (7.14), имеет вид, изображенный на рис. 7.14,

а условие устойчивости релейной системы связью (7.21) принимает вид

k			T T		k k		−	πb
	ос			1 2		3
			T	+ T	1			2ck
									2
			1	2

с линейной обратной

. (7.23)

Рис. 7.14

В соответствии с этим устойчивости на плоскости k2k

ос

на рис. 7.15 изображена область в случае линейной обратной связи.

Рис. 7.15

Аналогично на основании выражения (7.20) запишем условие устойчивости релейной системы с нелинейной обратной связью:

1 −		T1T2	k k	−	8kосk2	aq(a) k		q(a) 0 .
							2
			1 3
	T1 + T2				3πf (a)

Здесь также надо потребовать удовлетворения этого условия при

179

наибольшем значении q kос где

(a)

 

. Условие устойчивости примет вид

T T				πb			3π	2	f
1	2	k1k3	−							1	,	(7.24)
T + T				2ck			32ck
					2					2
1	2

				T T
f	1	=	1 −	1	2
				T + T
				1	2

				2c	2	2c
k k		k			+		(T	+ T	)T T k k		k
	2		3							2		3
1							1	2	1 2 1
				πb		πb

.

Поскольку в первом пропорциональна величине

грубом

ck	2	, то

приближении величина

f1

характер очертания границы

устойчивости сохранится. Если при этом множитель за скобкой в выражении (7.24) можно сделать меньшим единицы, то за счет нелинейности обратной связи можно расширить область устойчивости, как показано на рис. 7.15.

7.3. Псевдолинейная коррекция

Псевдолинейными корректирующими устройствами

называются такие нелинейные корректирующие устройства, у которых эквивалентные передаточные функции (а значит, и коэффициенты гармонической линеаризации), в отличие от рассмотренных в предыдущем параграфе, зависят только от частоты и не зависят от амплитуды. Однако эта зависимость от частоты – нелинейная в том смысле, что характер ее отличается от частотной зависимости линейных передаточных функций и может быть произвольным, т. е. отсутствует жесткая связь между амплитудными и фазовыми характеристиками, которая имеется у линейных звеньев. Это важное достоинство псевдолинейных устройств позволяет корректировать фазовые соотношения независимо от амплитудных и наоборот, что невозможно сделать линейными средствами.

Результат гармонической линеаризации при исследовании устойчивости для псевдолинейного устройства F (x) имеет вид

	F (x) =		q(ω) +	q (ω)
				ω

	p		x

,

а при исследовании колебательных переходных процессов

180

	F (x) =		q(ω) +	q (ω)	( p − ξ)		x .
				ω

Эти выражения можно представить в другой форме:

= k (ω)

F (x) T (ω) p +1 x ,

где для исследования устойчивости имеем

q

2

(ω) + q

2

(ω)

− q (ω)

k

=

,

T

=

,

q(ω)

ω q(ω)

а для колебательных переходных процессов

k =	q2 (ω)q 2 (ω)			,	T =	− q (ω)				.
		ξ					ξ
	q(ω) +	ω	q (ω)			ω q(ω) +		q (ω)
							ω

(7.25)

(7.26)

(7.27)

Такие псевдолинейные корректирующие устройства тоже обладают большими дополнительными возможностями улучшения качества процессов управления по сравнению с линейными устройствами.

Приведем несколько примеров.

Пример 7.4. Коррекция апериодического звена. Ставится задача существенного уменьшения инерционности, т. е. отставания

выходного сигнала по фазе ψ = arctgT , апериодического звена
(Tp +1) y = kx .	(7.28)

Решение. В одной из возможных схем такой коррекции (рис. 7.16, а) при помощи ключа отсекаются хвостовые части выходного сигнала, причем последний приобретает форму, показанную штриховкой на рис. 7.16, б. Тогда выражения для коэффициентов гармонической линеаризации примут вид

	q =	k cos ψ	[cos ψ(π −
		π

где ψ = arctgT . Видно, что

ω , но не от амплитуды, корректирующих устройств.

ψ) + sinψ],		=	k sin 2ψ	(ψ − π) ,
	q		2π

q и q будут зависеть лишь от частоты что характерно для псевдолинейных

181

а

б

Рис. 7.16

Применяя другую форму гармонической линеаризации (7.25), получим для скорректированного апериодического звена вместо (7.28) уравнение

[T		(ω) p +1]y =

в котором новые эквивалентные,

k		(ω)x ,

постоянная времени

T

и

коэффициент усиления через найденные уже q

k
(ω

,

)

определяются формулами (7.26) или (7.27)

и
	q (ω) . На рис. 7.17 приведены графики

их зависимости от частоты. Видно существенное снижение инерционности, например, при ωT = 2 получается примерно

T

= 0,5T

, но при этом примерно во столько же раз снижается и

усиление k		.
Таким способом можно уменьшать фазовое запаздывание в тех

звеньях системы, которые обладают большой постоянной времени, плохо влияющей на качество процесса управления.

182