2 курс ОАУ(ТАУ) [препод. Петунин В.И.] / Лекции / 10

10.КОСВЕННЫЕ МЕТОДЫ ОЦЕНКИ КАЧЕСТВА САУ

10.1.Корневые методы оценки качества переходных процессов

10.1.1.Корневые оценки. Вид корней характеристического уравнения определяет характер переходной составляющей процесса управления

n

xс(t) Сie pit.

i 1

Следовательно, корни уравнения могут являться мерой качества системы управления. Поэтому можно сформулировать требования по запасу устойчивости и быстродействию системы, не рассматривая самих переходных процессов, а накладывая определенные условия на корни характеристического уравнения.

Пусть характеристическое уравнение системы имеет вид

где p c jω – комплексное число.

Используя понятие среднегеометрического корня

где p1, p2, , pn – корни характеристического уравнения, в (10.1) можно перейти к новой комплексной величине q путем подстановки

pΩ0q.

Врезультате получим уравнение

в котором безразмерные коэффициенты A1, A2, , An 1 определяются выражением

a n k

Ak k 0 , (10.4) a0

а его корни равны q1 p1 / 0, q2 p2 / 0 и т. д.

Исходное характеристическое уравнение (10.1) при возвращении к прежней комплексной величине получает вид

быстроты протекания переходных процессов. Если в уравнении (10.5)

211

увеличить 0, например, в 10 раз, то на основании теоремы подобия переходный процесс, оставаясь подобным сам себе, будет протекать

в10 раз быстрее.

Всвязи с этим можно рассматривать (10.3) как некоторое нормированное характеристическое уравнение, которому соответствует переходный процесс, построенный для безразмерного времени t0 0t. Если качество переходного процесса является

приемлемым с точки зрения допустимого запаса устойчивости, определяемого, например, перерегулированием, то требуемая быстрота протекания переходного процесса может быть обеспечена соответствующим выбором величины 0.

Для увеличения величины 0, как следует из (10.2), необходимо увеличивать свободный член характеристического уравнения an. Напомним, что в статических системах an 1 K, а в астатических an K , где K – общий коэффициент усиления по разомкнутой цепи регулирования. Следовательно, повышение быстродействия может осуществляться за счет увеличения общего коэффициента усиления.

Для оценки быстродействия системы может использоваться понятие степени устойчивости.

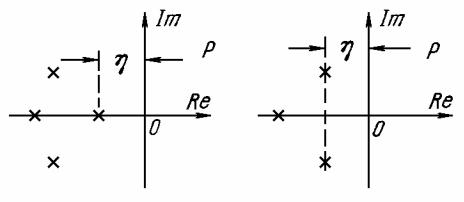
Под степенью устойчивости η понимается абсолютное значение вещественной части ближайшего к мнимой оси корня (рис. 10.1)

η |αi |min ,

где pi αi или pi,i 1 αi jβi .

а б Рис. 10.1

212

Термин «степень устойчивости» не является удачным, и его, вообще говоря, следовало заменить термином «степень быстродействия». Однако этот термин используется в литературе.

Здесь могут быть два случая: когда ближайший корень является вещественным (см. рис. 10.1, а) и когда к оси мнимых ближе всего расположена пара комплексных корней (см. рис. 10.1, б).

Корни характеристического уравнения, расположенные ближе всего к мнимой оси, т. е. имеющие наименьшую по абсолютной величине вещественную часть, дают в переходном процессе члены, которые затухают наиболее медленно. В большинстве случаев переходный процесс можно считать закончившимся тогда, когда затухнет член, определяемый ближайшим к мнимой оси корнем. Если ближайшим к мнимой оси является вещественный корень pi α, то составляющая в переходном процессе, определяемая этим корнем, будет иметь вид

xη(t) Cηe ηt.

Положив в конце переходного процесса xη(tп) Cη, где

0,01 0,05, можно получить приближенную зависимость между степенью устойчивости и временем переходного процесса:

Если ближайшей к мнимой оси является пара комплексных корней pi,i 1 α jβ, то составляющая в переходном процессе,

определяемая этими корнями, будет

xη(t) Cηe ηt sin(βt ψ).

Положив в этом случае xη(tп) Cη, нельзя в общем виде

определить время переходного процесса, так как для этой цели потребовалось бы решить трансцендентное уравнение. Однако можем найти верхнюю границу переходного процесса, положив в этом уравнении sin(βt ψ) 1. Тогда получим выражение

213

Таким образом, и в этом случае величина степени устойчивости будет в какой-то мере определять быстроту затухания переходного процесса.

Важным обстоятельством является то, что степень устойчивости можно найти без вычисления значений корней характеристического уравнения. При этом необходимо составление смещенного уравнения и применение критерия устойчивости к смещенному уравнению.

Для этой цели переходят к новой переменной z p η. Подставляя в характеристическое уравнение p z η, получаем так называемое смещенное уравнение

Это уравнение соответствует смещению осей на плоскости корней (см. рис. 10.1) влево на величину η. В результате один (см. рис. 10.1, а) или два (см. рис. 10.1, б) корня попадают на мнимую ось, что соответствует границе устойчивости.

Для вычисления степени устойчивости необходимо применить к смещенному характеристическому уравнению (10.8) любой критерий устойчивости и определить, при каком значении η получается граница устойчивости. Напомним, что апериодической границе устойчивости соответствует равенство нулю свободного члена характеристического уравнения:

а колебательной границе устойчивости соответствует равенство нулю предпоследнего определителя Гурвица, прохождение кривой Михайлова через начало координат и прохождение амплитуднофазовой характеристики разомкнутой системы через точку ( 1, j0).

Обратимся теперь к оценке запаса устойчивости системы автоматического регулирования. Склонность системы к колебаниям

214

будет наблюдаться, если в решении характеристического уравнения будут присутствовать комплексные корни вида pi,i 1 α jβ. Эта

склонность может характеризоваться отношением мнимой части корня (угловой частоты колебаний) к вещественной (коэффициенту затухания), которое называется колебательностью:

β μ . (10.10)

α max

Колебательность связана с другим корневым показателем запаса устойчивости – с так называемым затуханием ζ. Комплексные сопряженные корни дают в выражении для переходного процесса член вида

x(t) Ce αt sin(βt ψ).

Найдем затухание амплитуды синусоидального колебания за

1 ζ

Отсюда следует, что затухание ζ и колебательность μ связаны однозначной зависимостью. Чем меньше μ, тем больше ζ и запас устойчивости системы.

215

Обычно в системах автоматического регулирования допускается затухание за один период не менее чем 90…98%. Так, например, если ζ% 98%, то допустимая колебательность при этом составит

Задание определенной колебательности заставляет ограничивать область расположения корней двумя лучами (рис. 10.2, а), которые составляют с вещественной осью угол

а б

Рис. 10.2

Колебательность системы можно определить без нахождения корней характеристического уравнения подобно тому, как это было сделано выше по отношению к степени устойчивости. Идея метода

заключается в том, что используется подстановка p jze j , которая соответствует повороту координатных осей (см. рис. 10.2, а) против

часовой стрелки на угол π . При этом по крайней мере один

2

корень попадает на мнимую ось и затем он отыскивается. Ввиду громоздкости этот метод почти не имеет практического значения.

216

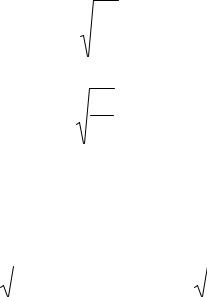
При задании допустимых значений колебательности и степени устойчивости область расположения корней должна ограничиваться также вертикальной прямой, проходящей параллельно оси мнимых на расстоянии η (см. рис. 10.2, б). Расположению корней в этой области соответствует выдерживание требуемого запаса устойчивости, определяемого величиной колебательности μ или затуханием, и требуемой степени устойчивости η, характеризующей быстродействие системы.

Для определения параметров системы, при которых обеспечивается нахождение корней характеристического уравнения в заданной области, можно воспользоваться D-разбиением. В этом случае в плоскости двух параметров системы может быть построена область, аналогично построению области устойчивости.

Наиболее просто это можно сделать для системы третьего порядка.

10.1.2. Диаграмма Вышнеградского. Корневые условия устойчивости системы третьего порядка были впервые сформулированы И. А. Вышнеградским еще в 1876 году, до появления в 1895 году критерия А. Гурвица.

Рассмотрим характеристическое уравнение третьего порядка

a0 p3 a1p2 a2 p a3 0. (10.14)

Приведем его к нормированному виду. Для этого разделим все члены на a3 и введем новую переменную

Здесь использовано понятие среднегеометрического корня:

0 3 a3 .

a0

В результате получим нормированное уравнение

называются параметрами Вышнеградского.

217

Условия устойчивости:

A 0, B 0 и AB 1.

На плоскости параметров A и B нанесем границу устойчивости. Уравнение границы устойчивости (колебательной):

AB 1 при A 0 и B 0.

Это есть равнобокая гипербола, для которой оси координат служат асимптотами (рис. 10.3). Область устойчивости системы, согласно написанным выше условиям, лежит выше этой кривой.

Рис. 10.3

Разобьем область устойчивости на отдельные части, соответствующие различному расположению корней характеристического уравнения. Заметим, что в точке C, где A B 3, характеристическое уравнение (10.16) принимает вид

(q 1)3 0. Следовательно, в этой точке все три корня равны: q1 q2 q3 1. При этом для исходного характеристического уравнения согласно (10.14) получаем

218

p1 p2 p3 3 a3 0. a0

В общем случае возможны два варианта: 1) все три корня вещественные; 2) один корень вещественный и два комплексных.

Граница между этими двумя случаями определяется равенством нулю дискриминанта уравнения третьей степени (10.16), который может быть получен, например, из формулы Кардана для решения кубического уравнения

A2B2 4(A3 B3) 18AB 27 0.

Это уравнение дает на плоскости параметров A, B две кривые: CE и CF (см. рис. 10.3). Внутри области ECF дискриминант положителен. Следовательно, в этой области имеется три вещественных корня (область III ). В остальной части плоскости дискриминант отрицателен, что соответствует наличию пары комплексных корней.

Существенное значение имеет взаимное расположение вещественного и комплексных корней. Будем различать здесь два случая: I – пара комплексных корней лежит ближе к мнимой оси, чем вещественный, и II – вещественный корень лежит ближе к мнимой оси, чем пара комплексных. Границей между этими двумя случаями является расположение всех трех корней на одинаковом расстоянии от мнимой оси. Уравнение этой границы можно найти,

В результате совместного решения последних трех равенств получаем после исключения α и β искомое уравнение, соответствующее граничному случаю:

2A3 9AB 27 0, A 3.

Написанное равенство дает на плоскости параметров кривую

CD.

219

Врезультате область устойчивости разбивается на три части: I , II, III (см. рис. 10.3). Этот график называется диаграммой Вышнеградского. Он построен им в 1876 году в работе, которая положила начало развитию теории автоматического регулирования.

На рис. 10.3 показан характер расположения корней внутри каждой из этих частей области устойчивости.

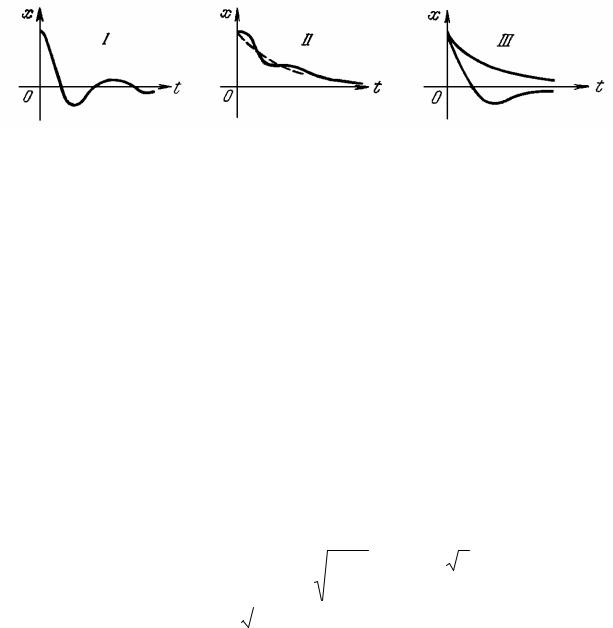
Вобласти III , где все корни вещественные, в зависимости от начальных условий получим апериодический переходный процесс в одной из форм, показанных на третьем графике рис. 10.4. Область III носит название области апериодических процессов.

Рис. 10.4

В областях I и II, где имеется один вещественный корень и два комплексных, переходный процесс будет иметь соответственно формы, показанные на первых двух графиках рис. 10.4. В области I быстрее затухает экспонента и переходный процесс в основном будет определяться колебательной составляющей. Это будет область колебательных процессов. В области II, наоборот, быстрее затухает колебательная составляющая. Это будет область монотонных процессов.

Пример 10.1. Дано характеристическое уравнение замкнутой системы автоматического управления

p2 p 1 0.

Определить корневые оценки качества системы. Решение. Корни характеристического уравнения:

220