
билеты под шпоры
.docxНесовместные и попарно-несовместные события. Свойства плотности распределения.
Полная группа событий. Плотность распределения вероятностей.
Пространство элементарных событий. X – непрерывная случайная величина,
 .
.Случайное событие. Достоверное событие. Свойства функции распределения вероятностей.
Сумма, разность и произведение случайных событий. Квантиль
Правило умножения вероятностей. X – дискретная случайная величина,

Правило сложения вероятностей. Случайная величина
Классическое и геометрическое определение вероятности. Правило «трех сигм».
Статистическое определение вероятности. Непрерывная случайная величина.
Условная вероятность. Дискретная случайная величина.
Свойства вероятности. Функция распределения вероятностей.
Локальная теорема Муавра-Лапласа. Закон распределения вероятностей.
Независимые события. Математическое ожидание дискретной с.в.
Аксиоматическое определение вероятности. Мода распределения.
Формула полной вероятности. Математическое ожидание непрерывной с.в.
Схема Бернулли. Медиана распределения.
Формула Бернулли. Дисперсия.
Формула Байеса. Свойства математического ожидания.
Правило умножения вероятностей. Среднеквадратическое отклонение.
Теорема Пуассона. Свойства дисперсии.
Формула Байеса. Ассиметрия.
Интегральная теорема Муавра-Лапласа. Центральный и абсолютный центральный момент k-го порядка
Свойства вероятности. Биномиальное распределение.
Закон больших чисел (идея). Эксцесс.
Пространство элементарных событий. Геометрическое распределение.
Центральная предельная теорема. Распределение Пуассона.
Аксиоматическое определение вероятностей. Экспоненциальное распределение.
Неравенство Маркова. Равномерное распределение.
Правило сложения вероятностей. Функция распределения для нормального закона.
Неравенство Чебышева. Нормальное распределение.
4
Случайное событие. Достоверное событие. Невозможное событие. Достоверное событие всегда происходит в результате наблюдения или испытания. Достоверное событие обозначается символом – W.
Невозможное событие никогда не происходит в результате наблюдения или испытания. Невозможное событие обозначается символом – Æ.
Пример Если в корзине только персики, то достать из корзины персик является достоверным событием, а достать лимон является невозможным событием.
Случайное событие – это такое событие, которое в результате наблюдения или испытания может произойти, а может и не произойти.
Пример Студент сдаёт экзамен. Экзамен сдан. Это событие случайное, так как студент мог и не сдать экзамен.
Свойства функции распределения вероятностей
Функция распределения лежит в пределах от 0 до 1 включительно

Функция распределения – неубывающая функция

Функция от минус бесконечности равна 0, от плюс бесконечности 1

Функция распределения непрерывна в любой точке

Вероятность попадания случайной величины в промежуток от a до b равна разности Функции распределения от b и Функции распределения от a

Это геометрическое представление совместной вероятности двух событий P(X<x,Y<y). Прямоугольник B – это 2 интервала, по горизонтали – крайние значения интервала для события X, по вертикали – для Y.
Чтобы определить вероятность попадания в интервал, необходимо посмотреть, какие значения X и Y попадают в соответствующий для каждой переменной интервала и сложить соответствующие вероятности.
Несмещенная выборочная дисперсия Количество элементов n, делённое на n-1 и умноженное на найденную выборочную дисперсию называется несмещённой выборочной дисперсией

 7
7
Правило сложения вероятностей


Случайная величина
Под случайной величиной понимают величину, которая в результате опыта принимает то или иное значение, причем неизвестное заранее, какое именно. Могут быть дискретными и непрерывными. У дискретной количество значений счётно, у непрерывной – несчётно.
Дисперсия двумерной дискретной с.в.
Дисперсия системы с.в. (X,Y):

Если
(X,Y) – система
дискретных случайных величин

Свойства точечных оценок
При точечном оценивании, указывается конкретное значение
параметра:

При небольшом объеме выборки замена неизвестного параметра его оценкой может приводить к большой погрешности, которая должна уменьшаться с ростом n
К оценке любого параметра предъявляется ряд требований.
Три свойства точечных оценок, которые говорят, что оценка качественная и ей можно доверять: cостоятельность, несмещенность, эффективность.
Оценка
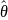 параметра
параметра
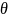 называется состоятельной,
если она сходится по вероятности к
оцениваемому параметру при
называется состоятельной,
если она сходится по вероятности к
оцениваемому параметру при



Т.е. с увеличением объема выборки качество оценки улучшается. Свойство состоятельности является обязательным для любого правила оценивания (несостоятельные оценки не рассматриваются).
Оценка
параметра
называется несмещенной,
если она в среднем совпадает с
т.е.

Если
 ,
то оценка называется смещенной.
,
то оценка называется смещенной.
Если
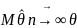 ,
то оценка называется асимптотически
несмещенной.
Требование
несмещенности важно при небольшом числе
испытаний.
,
то оценка называется асимптотически
несмещенной.
Требование
несмещенности важно при небольшом числе
испытаний.
Несмещенная оценка параметра называется эффективной, если она имеет наименьшую дисперсию среди всех несмещенных оценок параметра .
Т.е. оценка эффективна, если ее дисперсия минимальна.
10
Условная вероятность
Пусть случайное событие A может происходить при различных случайных условиях
Вероятность
случайного события A при
условии, что произошло случайное событие
B≠ называется условной вероятностью
события A, она обозначается
называется условной вероятностью
события A, она обозначается
 и вычисляется по формуле:
и вычисляется по формуле:

Дискретная случайная величина
ДСВ – это случайная величина, принимающая конечное или счетное множество значений.
Если множество возможных значений с.в. X конечно или счётно (это значит что его элементы могут быть пронумерованы натуральными числами), т.е. дискретно, то с.в. X называется дискретной (коротко: д.с.в. X).
Математическое ожидание двумерной непрерывной с.в.
Считается как двойной интеграл в пределах минус бесконечность плюс бесконечность для обоих переменных от совместной плотности распределения, умноженной на y или x, в зависимости от того, математическое ожидание какой величины вычисляется

Состоятельность точечной оценки
Оценка параметра называется состоятельной, если она сходится по вероятности к оцениваемому параметру при
Т.е. с увеличением объема выборки качество оценки улучшается. Свойство состоятельности является обязательным для любого правила оценивания (несостоятельные оценки не рассматриваются).
15
Формула полной вероятности

Математическое ожидание непрерывной с.в.
Математическое
ожидание непрерывной с.в. X
с плотностью распределения
 называется число:
называется число:

если этот интеграл абсолютно сходится
Плотность распределения вероятностей
П.Р.В.
непрерывной случайной величины (X,Y)
называется функция
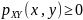 ,
т.ч.
,
т.ч.

или
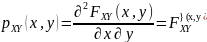
Таким образом

Доверительный интервал для математического ожидания нормального распределения при известном
 .
.

Где
 – значение аргумента функции Лапласа
при:
– значение аргумента функции Лапласа
при:

1
Несовместные и попарно-несовместные события.
Случайные события А и В называются несовместными, если при данном испытании появление одного из них исключает появление другого события. Несовместные события: день и ночь, студент одновременно едет на занятие и сдаёт экзамен, число иррациональное и чётное.
"Попарно" означает, что все возможные события разбиты на пары, и совместимость/несовместимость имеет место в каждой паре событий НЕЗАВИСИМО от других пар. Т. е. если произошло событие, то другое событие из той же пары - невозможно. При этом то, какое из двух событий произошло, не влияет на другие пары событий.
Пример: идёт дождь - безоблачное небо; инфляция возросла - цены упали.
Эти события - попарно несовместимы - если идёт дождь - не может быть безоблачного неба и наоборот.
Свойства плотности распределения вероятностей.
 (неотрицательность)
(неотрицательность) (нормированность)
(нормированность)


Для двумерной
Неотрицательность:

Нормированность:



Совместная функция распределения многомерной с.в.
С.Ф.Р. двумерной с.в. ( X ,Y ) (или двумерной функцией распределения случайного вектора) называется функция:

Выборочная дисперсия.

26
Центральная предельная теорема (идея)
ЦПТ устанавливает предельные распределения с.в.
Группа теорем, которые устанавливают, что при достаточно общих и естественных условиях закон распределения суммы большого числа с.в. близок к нормальному.
Частный случай – предельные теоремы в схеме Бернулли
Распределение Пуассона

Свойства ковариации
Выборка
Выборка – это последовательность
 независимых одинаково распределенных
с.в., распределение каждой из которых
совпадает с распределением генеральной
совокупности.
независимых одинаково распределенных
с.в., распределение каждой из которых
совпадает с распределением генеральной
совокупности.
29
Правило сложения вероятностей

Функция распределения для нормального закона

Математическое ожидание двумерной непрерывной с.в.
Метод моментов
Идея: приравнивание теоретических и выборочных моментов.
Если необходимо оценить параметров получим систему:
Или можно рассматривать не центральные моменты:
 25
25
Пространство элементарных событий
ПЭС - множество всех возможных взаимоисключающих исходов опыта.
Обозначается:
 𝑖
𝑖
 - элементарные (неделимые) события,
которые нельзя (или не имеет смысла)
разбить на более простые.
- элементарные (неделимые) события,
которые нельзя (или не имеет смысла)
разбить на более простые.
 – достоверное событие:
– достоверное событие:
 ,
n – из формулы (1) число
элементов
,
n – из формулы (1) число
элементов
Геометрическое распределение
Случайная величина X – число испытаний до первого успеха в схеме Бернулли имеет геометрическое распределение с законом:
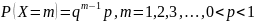

Коэффициент корреляции
Коэффициентом корреляции с.в. X, Y называется нормированный смешанный центральный момент 2-ого порядка, т.е.:

Размах выборки и интервал варьирования
Размах
-
 -
разность между максимальным и минимальным
значением.
-
разность между максимальным и минимальным
значением.
Интервал
варьирования –

24
Закон больших чисел (идея)
ЗБЧ – устанавливает предельные значения с.в.
Группа теорем, которые устанавливают устойчивость средних значений: при большом числе испытаний (в которых с.в. будет принимать различные значения) среднее значение всех результатов перестает быть случайным и может быть предсказано с достаточной точностью. Это утверждение остается верным и при наблюдении за различными с.в., имеющими различные распределения.
Эксцесс
Нормированный центральный момент 4-ого порядка называется эксцессом:

Эксцесс характеризует выраженность вершины распределения.
Плотность распределения многомерной с.в.
Называется функция , т.ч.

Таким образом (НЕ ОБЯЗАТЕЛЬНО *наверное*)
Реализация выборки
Реализация выборки – это конкретные
значения выборки, полученные в результате
наблюдений

23
Свойства вероятности
1.

2.

3.

4.

5.

6.

7.
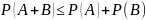
Биномиальное распределение (распределение Бернулли)

Случайная величина X – число успехов в схеме Бернулли имеет биномиальное расределение с законом:


Ковариация
Ковариацией с.в. X,Y называется смешанный центральный момент 2-ого порядка, т.е.:

Ковариация является мерой линейной
зависимости между с.в., т.е.
 тогда и только тогда, когда с.в. линейно
зависимы.
тогда и только тогда, когда с.в. линейно
зависимы.
Генеральная совокупность
Генеральная совокупность
– это с.в.
 ,
т.е. множество всех возможных ее значений
или все теоретически возможные результаты
наблюдений (опыта).
,
т.е. множество всех возможных ее значений
или все теоретически возможные результаты
наблюдений (опыта).
22
Интегральная теорема Муавра-Лапласа.
Если
 ,
то
,
то

Центральный и абсолютный центральный момент k-го порядка
Центральный момент k-ого
порядка:

Абсолютный:
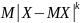
Плотность распределения функции от случайной величины


Вариационный ряд выборки
Вариационный ряд:

20
Теорема Пуассона
Если
 ,
то
,
то

Свойства дисперсии



Если с.в.
 – независимы, то
– независимы, то

Независимость случайных величин
C.в.
 называются независимыми, если
называются независимыми, если

Дискретные с.в. независимы тогда и только тогда, когда

Непрерывные с.в. независимы тогда и только тогда, когда

Доверительный интервал для математического ожидания нормального распределения при неизвестно

Где
 -
находится по таблицам распределения
Стьюдента с n-1 степенью
свободы
-
находится по таблицам распределения
Стьюдента с n-1 степенью
свободы
21
Формула Байеса
Если событие А произошло, то априорные вероятности гипотез Р(Нi) должны быть заменены на апостериорные, вычисленные по формуле Байеса:

Асимметрия
Нормированный центральный момент 3-го порядка называется асимметрией:

Это геометрическое представление
совместной вероятности двух событий
 ).
Прямоугольник B – это 2 интервала, по
горизонтали – крайние значения интервала
для события X, по вертикали – для Y.
).
Прямоугольник B – это 2 интервала, по
горизонтали – крайние значения интервала
для события X, по вертикали – для Y.
Чтобы определить вероятность попадания в интервал, необходимо посмотреть, какие значения X и Y попадают в соответствующий для каждой переменной интервала и сложить соответствующие вероятности.
Ранг элемента выборки
Ранг – номер элемента в вариационном ряду (если есть несколько одинаковых элементов, то считается средний ранг).
17
Формула Бернулли


Дисперсия
Дисперсия – математическое ожидание квадрата её отклонения от математического ожидания:

Если с.в. X дискретная, то

Если с.в. X непрерывная, то

Дисперсия характеризует разброс значений с.в. относительно её математического ожидания, её размерность совпадает с размерностью квадрата с.в.
Плотность распределения многомерной с.в.
Называется функция , т.ч.
Таким образом (НЕ ОБЯЗАТЕЛЬНО *наверное*)
Доверительный интервал для параметра распределения Пуассона.
 12
12
Локальная теорема Муавра-Лапласа
Если
с.в. X – число успехов в
схеме Бернулли, величина
 равномерно ограничена по m
и по n, то
равномерно ограничена по m
и по n, то

где

Закон распределения вероятностей
Рассмотрим
дискретную двумерную с.в. (X,Y),
которая может принимать значения
 .
Тогда закон распределения вероятностей
указывает совместную вероятность каждой
возможной пары значений:
.
Тогда закон распределения вероятностей
указывает совместную вероятность каждой
возможной пары значений:

Причем

Функция от случайной величины
От непрерывной с.в.
Если
с.в. X – непрерывна с
плотностью
,
а функция
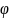 - дифференцируема и монотонна, то
плотность распределения с.в.
выражается формулой:
- дифференцируема и монотонна, то
плотность распределения с.в.
выражается формулой:
От дискретной с.в.
Если с.в. X дискретная с законом распределения

Если с.в. также будет дискретной с законом:

Эффективность точечной оценки
Несмещенная оценка параметра называется эффективной, если она имеет наименьшую дисперсию среди всех несмещенных оценок параметра .
Т.е. оценка эффективна, если ее дисперсия минимальна
Эффективную оценку можно найти в ряде случаев, используя неравенство Рао-Крамера:

19
Правило умножения вероятностей

Среднеквадратическое отклонение
Среднеквадратическим отклонением с.в. X называется:

Cреднеквадратическое отклонение тоже характеризует разброс значений с.в., но его размерность совпадает с размерностью с.в.
Функция от случайной величины
От непрерывной с.в.
Если с.в. X – непрерывна с плотностью , а функция - дифференцируема и монотонна, то плотность распределения с.в. выражается формулой:
От дискретной с.в.
Если с.в. X дискретная с законом распределения
Если с.в. также будет дискретной с законом:
Свойства точечных оценок
При точечном оценивании, указывается конкретное значение
параметра:
При небольшом объеме выборки замена неизвестного параметра его оценкой может приводить к большой погрешности, которая должна уменьшаться с ростом n
К оценке любого параметра предъявляется ряд требований.
Три свойства точечных оценок, которые говорят, что оценка качественная и ей можно доверять: cостоятельность, несмещенность, эффективность.
Оценка параметра называется состоятельной, если она сходится по вероятности к оцениваемому параметру при
Т.е. с увеличением объема выборки качество оценки улучшается. Свойство состоятельности является обязательным для любого правила оценивания (несостоятельные оценки не рассматриваются).
Оценка параметра называется несмещенной, если она в среднем совпадает с т.е.
Если , то оценка называется смещенной.
Если , то оценка называется асимптотически несмещенной. Требование несмещенности важно при небольшом числе испытаний.
Несмещенная оценка параметра называется эффективной, если она имеет наименьшую дисперсию среди всех несмещенных оценок параметра .
Т.е. оценка эффективна, если ее дисперсия минимальна.
18
Формула Байеса
Если событие А произошло, то априорные вероятности гипотез Р(Нi) должны быть заменены на апостериорные, вычисленные по формуле Байеса:
Свойства математического ожидания



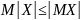

Если с.в. - независимы, то









