Шпаргалка Раздел 3 Двумерные случайные величины

1. Двумерная случайная величина.

Пусть X, Y – с.в., заданные на вероятностном пространстве ( ,U,P). Каждому элементарному событию эти с.в. ставят в соответствие двумерный вектор (X(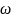 ), Y( )). Отображение задаваемое с.в. (X,Y) называется двумерной случайной величиной (случайным вектором, системой с.в.).

2. Совместная функция распределения двумерной с.в.

Совместной функцией распределения двумерной с.в. (X,Y) (или двумерной функцией распределения случайного вектора) называется функция:

Геометрическая интерпретация: F_XY(x,y) показывает вероятность попадания в случайный угол.

3. P(a₁<X<b₁, a₂<Y<b₂), (X,Y) – непрерывная с.в.

Это геометрическое представление совместной вероятности двух событий P(X<x,Y<y). Прямоугольник В – это два интервала, по горизонтали – крайние значения интервала для события Х, по вертикали – для Y.

P(a₁<X<b₁, a₂<Y<b₂) =

F_XY(b₁,b₂)-F_XY(a₁,b₂)-F_XY(b₁,a₂)+F_XY(a₁,a₂)

4. Закон распределения вероятностей двумерной дискретной с.в.

Рассмотрим дискретную двумерную с.в. (X,Y), которая может принимать значения X=x₁,K,x_n, Y=y₁,K,y_m. Тогда закон распределения вероятностей указывает совместную вероятность каждой возможной пары значений: P(X=x_i,Y=y_i)=p_ij, i= , j= , причем = 1.

xi\yj	y1		yj		ym	pij
x1	p11		p1j		p1m	p1
xi	pi1		pij		pim	pi
xn	pn1		pnj		pnm	pn
ij	p1		pj		pm	1

5. Плотность распределения двумерной с.в.

Плотностью распределения вероятностей непрерывной двумерной с.в. (X,Y) называется функция p_XY(x,y)>=0, т.ч. или p_XY(x,y)= =F_XY^’’(x,y)

Таким образом, F_XY(x,y)=

6. Независимость случайных величин

С.в. X,Y называются независимыми, если , F_XY(x,y)=F_X(x)F_Y(y)

Следствие: дискретные с.в. независимы тогда и только тогда, когда P(X=x_i, Y=y_j)=P(X=x_i)P(Y=y_j)

Непрерывные с.в. независимы тогда и только тогда, когда p_XY(x,y)=p_X(x)p_Y(y)

7. Математическое ожидание двумерной дискретной с.в.

MX=m_x= x_ip_ij, MY=m_y= y_jp_ij, (здесь p_ij=P{X=x_i, Y=y_j}).

8. Дисперсия двумерной дискретной с.в.

DX= (x_i-m_x)²p_ij, DY= (y_i-m_y)²p_ij

9. Математическое ожидание двумерной непрерывной с.в.

MX=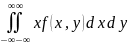 , MY= ,

если (X,Y) – непрерывная система с.в. (здесь f(x,y) – плотность распределения системы).

10. Дисперсия двумерной непрерывной с.в.

DX= ,

DY=

11. Функция от случайной величины

Пусть имеется вероятностное пространство ( ,U,P), и на нем задана с.в. X( ). Пусть также имеется некоторая функция y= (x). Этой функцией можно подействовать и на с.в. Х. В результате получим новую с.в.: Y= (X)= (X( ))

12. Математическое ожидание функции от с.в. Y= (X)

MY=M( (X))=

13. Дисперсия функции от с.в. Y= (X)

DY= D( (X))=

14. Плотность распределения функции от с.в. Y= (X)

P_Y(y)=p_x

15. Ковариация

Ковариацией р с.в. X, Y называется смешанный центральный момент 2-го порядка, т.е.:

cov(X,Y)=M[(X-MX)(Y-MY)]=M(XY)-MX*MY

16. Свойства ковариации

1. cov(X,Y)=cov(Y,X)

2. cov(cX,Y)=ccov(X,Y)

3. cov(c+X,Y)=cov(X,Y)

4. cov(X,X)=DX

5. cov(X,Y)<=DX*DY

6. Если с.в. X, Y независимы, то cov(X,Y)=0 (обратное неверно!)

17. Коэффициент корреляции

Коэффициентом корреляции с.в. X, Y называется нормированный смешанный центральный момент 2-го порядка, т.е.:

18. Свойства коэффициента корреляции

1. r(X,Y)=r(Y,X)

2. r(cX,Y)=r(X,Y)sign(c)

3. r(c+X,Y)=r(X,Y)

4. |r(X,Y)|<=1, |r(X,Y)|=1  X=kY+b

5. Если с.в. X, Y независимы, то r(X,Y)=0

19. Теорема Пуассона.

Если n , p 0, np =const≠0, то P(X=m)=C_n^mp^mq^n-m .

На практике формулу Пуассона можно применять, если p<0.1, npq<10

20. Локальная теорема Муавра-Лапласа.

Если с.в. Х – число успехов в схеме Бернулли, величина x_m=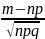 равномерно ограничена по m и n, то P(X=m)= , где – функция Гаусса, , c > 0

21. Интегральная теорема Муавра-Лапласа.

Если n , p=const, p (0,1), то

P(a<X<b)

P(a< <b) .

22. Закон больших чисел (идея).

ЗБЧ устанавливает устойчивость средних значений: при большом числе испытаний их средний результат перестает быть случайным и может быть предсказан с достаточной точностью.

23. Центральная предельная теорема (идея).

ЦПТ устанавливает условия, при которых закон распределения суммы большого числа случайных величин неограниченно приближается к нормальному.

24. Неравенство Маркова.

Если с.в. Х принимает неотрицательные значения, то справедливо:

25. Неравенство Чебышева.

Если с.в. Х имеет конечную дисперсию, то справедливо: